MATLAB滤波器类型大揭秘：解锁不同滤波器的特性和应用，助你游刃有余

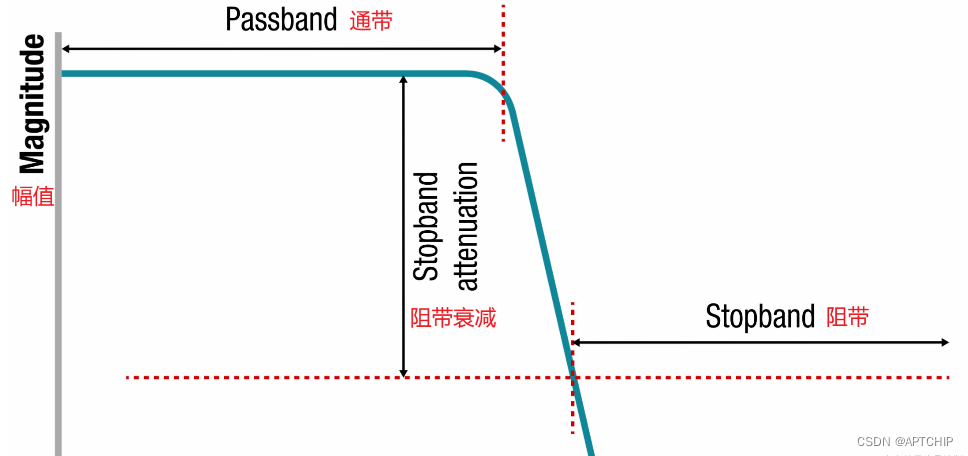
# 1. MATLAB滤波器概述

MATLAB滤波器是用于处理和分析信号的强大工具，它们能够去除噪声、提取特征并增强信号质量。MATLAB提供了各种滤波器类型，每种类型都有其独特的特性和应用场景。

滤波器可以根据其脉冲响应分为两大类：有限脉冲响应（FIR）滤波器和无限脉冲响应（IIR）滤波器。FIR滤波器具有线性相位响应，而IIR滤波器具有更陡峭的截止频率，但相位响应是非线性的。

# 2. 滤波器类型及其特性

### 2.1 FIR滤波器

**特性**

有限脉冲响应 (FIR) 滤波器是一种线性、时不变滤波器，其脉冲响应在有限时间内为零。这意味着 FIR 滤波器的输出仅取决于当前输入，而不依赖于过去的输入或输出。

FIR 滤波器的主要特性包括：

- **线性相位响应：** FIR 滤波器具有线性相位响应，这意味着它们不会引入相位失真。
- **稳定性：** FIR 滤波器始终是稳定的，因为它们的极点位于单位圆外。
- **易于设计：** FIR 滤波器易于设计，可以使用窗函数法或频域变换法。

**应用**

FIR 滤波器广泛用于各种应用中，包括：

- **音频信号处理：** FIR 滤波器用于均衡、降噪和回声消除。
- **图像处理：** FIR 滤波器用于图像锐化、去噪和边缘检测。
- **通信系统：** FIR 滤波器用于抗混叠和信道均衡。

### 2.2 IIR滤波器

**特性**

无限脉冲响应 (IIR) 滤波器是一种线性、时不变滤波器，其脉冲响应在无限时间内非零。这意味着 IIR 滤波器的输出不仅取决于当前输入，还取决于过去的输入和输出。

IIR 滤波器的主要特性包括：

- **非线性相位响应：** IIR 滤波器具有非线性相位响应，这意味着它们会引入相位失真。
- **可能不稳定：** IIR 滤波器可能不稳定，具体取决于其极点的位置。
- **难以设计：** IIR 滤波器比 FIR 滤波器更难设计，因为它们需要考虑极点和零点的位置。

**应用**

IIR 滤波器也广泛用于各种应用中，包括：

- **音频信号处理：** IIR 滤波器用于均衡、滤波和谐波合成。
- **控制系统：** IIR 滤波器用于反馈回路和状态估计。
- **地震学：** IIR 滤波器用于地震数据的处理和分析。

### 2.3 其他滤波器类型

除了 FIR 和 IIR 滤波器之外，还有其他类型的滤波器，包括：

- **陷波滤波器：** 陷波滤波器用于消除特定频率范围内的信号。
- **带通滤波器：** 带通滤波器用于仅允许特定频率范围内的信号通过。

**表格：滤波器类型比较**

| 特性 | FIR滤波器 | IIR滤波器 |
|---|---|---|
| 脉冲响应 | 有限 | 无限 |
| 相位响应 | 线性 | 非线性 |
| 稳定性 | 稳定 | 可能不稳定 |
| 设计难度 | 容易 | 困难 |
| 应用 | 音频信号处理、图像处理、通信系统 | 音频信号处理、控制系统、地震学 |

# 3. 滤波器设计与实现

### 3.1 滤波器设计方法

滤波器设计方法主要分为两类：窗函数法和频域变换法。

**3.1.1 窗函数法**

窗函数法是一种通过在理想滤波器的频率响应上加窗函数来设计滤波器的方法。常用的窗函数有矩形窗、汉明窗、海明窗等。窗函数法设计出的滤波器具有良好的幅度响应，但相位响应不理想。

**3.1.2 频域变换法**

频域变换法是一种通过将滤波器的频率响应变换到另一个域（如s域或z域）来设计滤波器的方法。常用的频域变换法有双线性变换、巴特沃斯-切比雪夫变换等。频域变换法设计出的滤波器具有良好的相位响应，但幅度响应可能不理想。

### 3.2 MATLAB中的滤波器设计函数

MATLAB中提供了丰富的滤波器设计函数，可以方便地设计出各种类型的滤波器。常用的滤波器设计函数有：

**3.2.1 fir1**

`fir1`函数用于设计有限脉冲响应（FIR）滤波器。该函数的语法为：

b = fir1(N,Wn,ftype)

其中：

* `N`：滤波器的阶数
* `Wn`：归一化截止频率（0-1）
* `ftype`：滤波器的类型（'low'、'high'、'bandpass'、'bandstop'）

**3.2.2 fir2**

`fir2`函数用于设计具有任意频率响应的FIR滤波器。该函数的语法为：

b = fir2(N,F,M,W)

其中：

* `N`：滤波器的阶数
* `F`：频率向量
* `M`：幅度响应
* `W`：权重向量

**3.2.3 butter**

`butter`函数用于设计巴特沃斯滤波器。该函数的语法为：

[b,a] = butter(N,Wn,ftype)

其中：

* `N`：滤波器的阶数
* `Wn`：归一化截止频率（0-1）
* `ftype`：滤波器的类型（'low'、'high'、'bandpass'、'bandstop'）

### 3.3 滤波器实现与应用

**3.3.1 滤波器的应用场景**

滤波器在信号处理中有着广泛的应用，包括：

* 噪声消除
* 特征提取
* 图像处理
* 语音处理
* 生物医学信号处理

**3.3.2 滤波器的参数设置**

滤波器的参数设置对滤波效果至关重要。常用的滤波器参数包括：

* 截止频率：滤波器通过或衰减信号的频率范围
* 阶数：滤波器的复杂程度
* 窗函数：用于设计FIR滤波器的窗函数
* 通带增益：滤波器在通带内的增益
* 阻带衰减：滤波器在阻带内的衰减

# 4. 滤波器在信号处理中的应用**

**4.1 噪声消除**

**4.1.1 噪声的类型**

噪声是信号处理中常见的干扰，它会掩盖有用信号，影响信号处理的准确性。噪声的类型多种多样，常见的有：

- **高斯噪声：**一种常见的噪声，其幅度分布符合正态分布。
- **白噪声：**一种功率谱密度在整个频率范围内均匀分布的噪声。
- **粉红噪声：**一种功率谱密度随频率降低而增加的噪声。
- **脉冲噪声：**一种由脉冲序列组成的噪声，通常由设备故障或数据传输错误引起。

**4.1.2 滤波器在噪声消除中的作用**

滤波器可以有效地消除噪声，提高信号的信噪比。滤波器的作用原理是根据噪声的频谱特性，选择合适的滤波器类型和参数，将噪声成分从信号中滤除。

**4.2 特征提取**

**4.2.1 特征提取的原理**

特征提取是信号处理中的一项重要任务，其目的是从原始信号中提取具有代表性的特征，用于分类、识别或其他分析任务。滤波器在特征提取中扮演着重要角色。

**4.2.2 滤波器在特征提取中的应用**

滤波器可以用来预处理信号，去除噪声或增强特定频率成分，从而提高特征提取的准确性。例如：

- **边缘检测：**使用高通滤波器增强图像边缘的对比度，便于边缘检测算法提取边缘特征。
- **语音识别：**使用梅尔滤波器组将语音信号分解成多个频段，提取每个频段的能量特征，用于语音识别。

**4.3 图像处理**

**4.3.1 图像处理中的滤波技术**

滤波技术在图像处理中广泛应用，主要用于图像增强、去噪和边缘检测等任务。常见的图像滤波技术包括：

- **平滑滤波：**使用均值滤波器或高斯滤波器平滑图像，去除噪声。
- **锐化滤波：**使用拉普拉斯滤波器或Sobel滤波器锐化图像，增强边缘。
- **形态学滤波：**使用膨胀、腐蚀等形态学操作对图像进行处理，提取特定形状或特征。

**4.3.2 滤波器在图像处理中的应用**

滤波器在图像处理中的应用十分广泛，包括：

- **图像增强：**去除噪声，增强对比度，提高图像的可视性。
- **图像去噪：**去除图像中的噪声，提高图像质量。
- **边缘检测：**提取图像中的边缘，用于目标识别或图像分割。
- **纹理分析：**分析图像中的纹理特征，用于图像分类或缺陷检测。

# 5. 滤波器优化与性能评估**

**5.1 滤波器优化方法**

滤波器的优化旨在提高其性能，满足特定的设计要求。常见的优化方法包括：

**5.1.1 滤波器阶数优化**

滤波器的阶数决定了其频率响应的复杂程度。较高的阶数可以提供更精确的频率响应，但也会增加计算成本。因此，选择合适的阶数非常重要。

**优化步骤：**

1. 使用滤波器设计函数（如 `fir1` 或 `butter`）设计一个初始滤波器。
2. 评估滤波器的频率响应，确定需要优化的频率范围。
3. 调整滤波器的阶数，并重新评估频率响应。
4. 重复步骤 2 和 3，直到达到满意的频率响应。

**5.1.2 窗函数选择优化**

窗函数用于平滑滤波器的频率响应，减少不必要的旁瓣。不同的窗函数具有不同的特性，因此选择合适的窗函数对于优化滤波器性能至关重要。

**优化步骤：**

1. 使用不同的窗函数（如矩形窗、汉明窗、凯撒窗）设计滤波器。
2. 比较不同窗函数的频率响应，评估其旁瓣抑制能力。
3. 选择具有最佳旁瓣抑制和频率响应特性的窗函数。

**5.2 滤波器性能评估指标**

为了评估滤波器的性能，需要使用以下指标：

**5.2.1 频率响应**

频率响应描述滤波器在不同频率下的幅度和相位响应。理想的频率响应应与设计要求相匹配，例如平坦的通带、陡峭的截止带和低的纹波。

**5.2.2 相位响应**

相位响应描述滤波器在不同频率下引入的相移。对于某些应用（如信号处理），相位响应的线性度非常重要。

**5.2.3 群延迟**

群延迟是信号通过滤波器所需的时间。理想的群延迟应恒定，以避免信号失真。