【MATLAB滤波宝典】：一站式掌握滤波技术，从入门到精通

# 1. MATLAB滤波基础**

MATLAB滤波是一种用于处理和分析数据的强大工具。滤波技术可以从数据中去除噪声、提取特征和增强信号。MATLAB提供了广泛的滤波函数，涵盖时域和频域滤波技术。

在MATLAB中，滤波器可以通过`filter`函数应用。该函数需要两个参数：滤波器系数和输入数据。滤波器系数定义了滤波器的频率响应，决定了滤波器的通带和阻带特性。输入数据可以是时域信号或频域信号。

# 2. 时域滤波技术

### 2.1 移动平均滤波

#### 2.1.1 原理和实现

移动平均滤波是一种简单而有效的时域滤波技术，它通过计算信号中相邻数据点的平均值来平滑信号。其基本原理如下：

y[n] = (1/N) * Σ[x[n-i] for i in range(0, N-1)]

其中：

* `y[n]` 是滤波后的信号
* `x[n]` 是原始信号
* `N` 是滤波窗口的大小

在MATLAB中，可以使用 `filter` 函数实现移动平均滤波：

y = filter(ones(1, N) / N, 1, x);

#### 2.1.2 优点和局限性

**优点：**

* 实现简单，计算量小
* 能有效去除高频噪声
* 保留信号的整体趋势

**局限性：**

* 会导致信号延迟
* 对于尖锐的信号变化，平滑效果不佳
* 无法去除低频噪声

### 2.2 中值滤波

#### 2.2.1 原理和实现

中值滤波是一种非线性滤波技术，它通过计算信号中相邻数据点的中值来平滑信号。其基本原理如下：

y[n] = median([x[n-i] for i in range(0, N-1)])

其中：

* `y[n]` 是滤波后的信号
* `x[n]` 是原始信号
* `N` 是滤波窗口的大小

在MATLAB中，可以使用 `medfilt1` 函数实现中值滤波：

y = medfilt1(x, N);

#### 2.2.2 优点和局限性

**优点：**

* 能有效去除椒盐噪声和脉冲噪声
* 对尖锐的信号变化有较好的平滑效果
* 不受离群值的影响

**局限性：**

* 计算量比移动平均滤波大
* 会导致信号边缘模糊
* 无法去除低频噪声

### 时域滤波技术对比

| 特征 | 移动平均滤波 | 中值滤波 |
|---|---|---|
| 滤波原理 | 计算相邻数据点的平均值 | 计算相邻数据点的中值 |
| 优点 | 实现简单，计算量小 | 能有效去除椒盐噪声和脉冲噪声 |
| 局限性 | 会导致信号延迟 | 计算量比移动平均滤波大 |
| 适用场景 | 去除高频噪声，保留信号整体趋势 | 去除椒盐噪声和脉冲噪声，处理尖锐信号变化 |

### 时域滤波应用示例

**移动平均滤波示例：**

% 原始信号
x = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10];

% 滤波窗口大小
N = 3;

% 滤波
y = filter(ones(1, N) / N, 1, x);

% 绘制原始信号和滤波后信号
plot(x, 'b-', y, 'r--');
legend('原始信号', '滤波后信号');
xlabel('时间');
ylabel('幅度');

**中值滤波示例：**

% 原始信号
x = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10];

% 滤波窗口大小
N = 3;

% 滤波
y = medfilt1(x, N);

% 绘制原始信号和滤波后信号
plot(x, 'b-', y, 'r--');
legend('原始信号', '滤波后信号');
xlabel('时间');
ylabel('幅度');

# 3.1 傅里叶变换

#### 3.1.1 原理和实现

傅里叶变换是一种数学变换，将时域信号转换为频域信号。它揭示了信号中不同频率成分的幅度和相位信息。

傅里叶变换的公式为：

X(f) = ∫_{-\infty}^{\infty} x(t) e^(-j2πft) dt

其中：

* X(f) 是频域信号
* x(t) 是时域信号
* f 是频率
* j 是虚数单位

傅里叶变换可以通过离散傅里叶变换（DFT）在计算机上实现。DFT将连续时域信号离散化为有限长度的序列，并使用快速傅里叶变换（FFT）算法进行计算。

#### 3.1.2 频谱分析

频谱分析是使用傅里叶变换来分析信号中不同频率成分的过程。频谱图显示了信号中每个频率的幅度和相位。

频谱分析在许多应用中很有用，例如：

* 识别信号中的噪声和干扰
* 提取信号中的特征
* 诊断设备和系统的问题

### 3.2 数字滤波器设计

#### 3.2.1 IIR滤波器

IIR（无限脉冲响应）滤波器是使用反馈回路实现的。它们具有无限长的脉冲响应，这意味着它们对输入信号的当前和过去值都做出反应。

IIR滤波器的优点包括：

* 可以实现复杂的滤波特性
* 比FIR滤波器更节省计算资源

IIR滤波器的缺点包括：

* 可能不稳定
* 具有相位失真

#### 3.2.2 FIR滤波器

FIR（有限脉冲响应）滤波器是使用抽头延迟线实现的。它们具有有限长的脉冲响应，这意味着它们只对输入信号的当前值做出反应。

FIR滤波器的优点包括：

* 总是稳定
* 没有相位失真

FIR滤波器的缺点包括：

* 实现复杂滤波特性需要更多计算资源
* 比IIR滤波器更长的延迟

# 4. 图像滤波应用

### 4.1 降噪

图像降噪是图像处理中的重要任务，旨在去除图像中不需要的噪声，提高图像质量。常用的图像降噪方法包括高斯滤波和中值滤波。

#### 4.1.1 高斯滤波

高斯滤波是一种线性滤波器，它使用高斯函数作为滤波核。高斯函数具有钟形曲线形状，中心权重最大，向两侧逐渐衰减。因此，高斯滤波可以有效地平滑图像，同时保留边缘和细节。

**原理和实现**

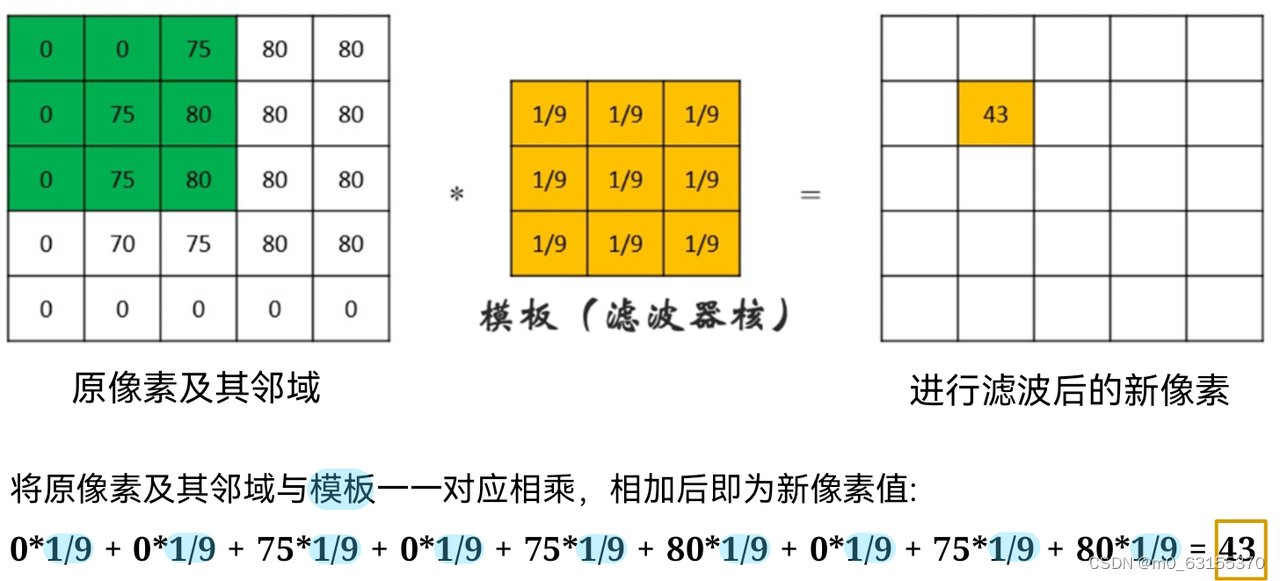
高斯滤波的原理是将图像中的每个像素值替换为其邻域像素值的加权平均值。权重由高斯函数决定，中心像素的权重最大，距离中心越远的像素权重越小。

MATLAB 中使用 `imgaussfilt` 函数进行高斯滤波。该函数接受图像和高斯核的标准差作为参数。标准差越大，滤波效果越强，图像越平滑。

% 读取图像
I = imread('image.jpg');

% 设置高斯核标准差
sigma = 2;

% 进行高斯滤波
J = imgaussfilt(I, sigma);

% 显示原图和滤波后图像
subplot(1,2,1); imshow(I); title('原图');
subplot(1,2,2); imshow(J); title('高斯滤波后图像');

**优点和局限性**

高斯滤波的优点包括：

* 平滑图像，同时保留边缘和细节
* 适用于各种类型的噪声
* 计算效率高

高斯滤波的局限性包括：

* 对于高频噪声效果不佳
* 可能导致图像模糊

### 4.1.2 中值滤波

中值滤波是一种非线性滤波器，它将图像中的每个像素值替换为其邻域像素值的中值。中值是邻域像素值排序后的中间值。因此，中值滤波可以有效地去除孤立噪声点，同时保留边缘和纹理。

**原理和实现**

中值滤波的原理是将图像中的每个像素及其邻域像素值排序，然后选择中间值作为该像素的新值。

MATLAB 中使用 `medfilt2` 函数进行中值滤波。该函数接受图像和滤波核大小作为参数。滤波核大小决定了邻域像素的范围。

% 读取图像
I = imread('image.jpg');

% 设置滤波核大小
kernelSize = 3;

% 进行中值滤波
J = medfilt2(I, kernelSize);

% 显示原图和滤波后图像
subplot(1,2,1); imshow(I); title('原图');
subplot(1,2,2); imshow(J); title('中值滤波后图像');

**优点和局限性**

中值滤波的优点包括：

* 有效去除孤立噪声点
* 保留边缘和纹理
* 对高频噪声效果好

中值滤波的局限性包括：

* 计算效率较低
* 可能导致图像细节丢失

# 5. 信号滤波应用**

### 5.1 信号去噪

#### 5.1.1 滑动平均滤波

滑动平均滤波是一种时域滤波技术，通过对信号的邻近数据点进行平均来平滑信号。其原理如下：

y = filter(ones(1, n) / n, 1, x);

其中：

- `x` 为输入信号
- `n` 为滤波器窗口大小
- `y` 为滤波后输出信号

滑动平均滤波的优点在于其简单易用，并且可以有效去除高频噪声。然而，其缺点是会引入延迟，并且可能导致信号失真。

#### 5.1.2 维纳滤波

维纳滤波是一种最优线性滤波器，其目标是通过最小化信号和噪声之间的均方误差来估计原始信号。其原理如下：

H = conj(X) ./ (X .* conj(X) + sigma^2);
y = ifft(H .* fft(x));

其中：

- `x` 为输入信号
- `sigma` 为噪声标准差
- `X` 为输入信号的傅里叶变换
- `H` 为维纳滤波器的频率响应
- `y` 为滤波后输出信号

维纳滤波的优点在于其可以有效去除噪声，同时保留信号的细节。然而，其缺点是需要知道噪声的统计特性，并且计算量较大。

### 5.2 信号增强

#### 5.2.1 高通滤波

高通滤波器通过允许高频信号通过，同时衰减低频信号来增强信号。其原理如下：

[b, a] = butter(n, cutoff_freq, 'high');
y = filter(b, a, x);

其中：

- `x` 为输入信号
- `n` 为滤波器阶数
- `cutoff_freq` 为截止频率
- `b` 和 `a` 为滤波器传递函数的系数
- `y` 为滤波后输出信号

高通滤波的优点在于其可以去除低频噪声，同时保留信号的高频成分。然而，其缺点是可能会引入振铃效应。

#### 5.2.2 带通滤波

带通滤波器通过允许特定频率范围内的信号通过，同时衰减其他频率的信号来增强信号。其原理如下：

[b, a] = butter(n, [low_cutoff_freq, high_cutoff_freq], 'bandpass');
y = filter(b, a, x);

其中：

- `x` 为输入信号
- `n` 为滤波器阶数
- `low_cutoff_freq` 和 `high_cutoff_freq` 为截止频率
- `b` 和 `a` 为滤波器传递函数的系数
- `y` 为滤波后输出信号

带通滤波的优点在于其可以有效去除特定频率范围内的噪声，同时保留信号的所需频率成分。然而，其缺点是可能会引入相位失真。