MATLAB滤波器最佳实践：掌握滤波技术中的黄金法则，成为滤波大师

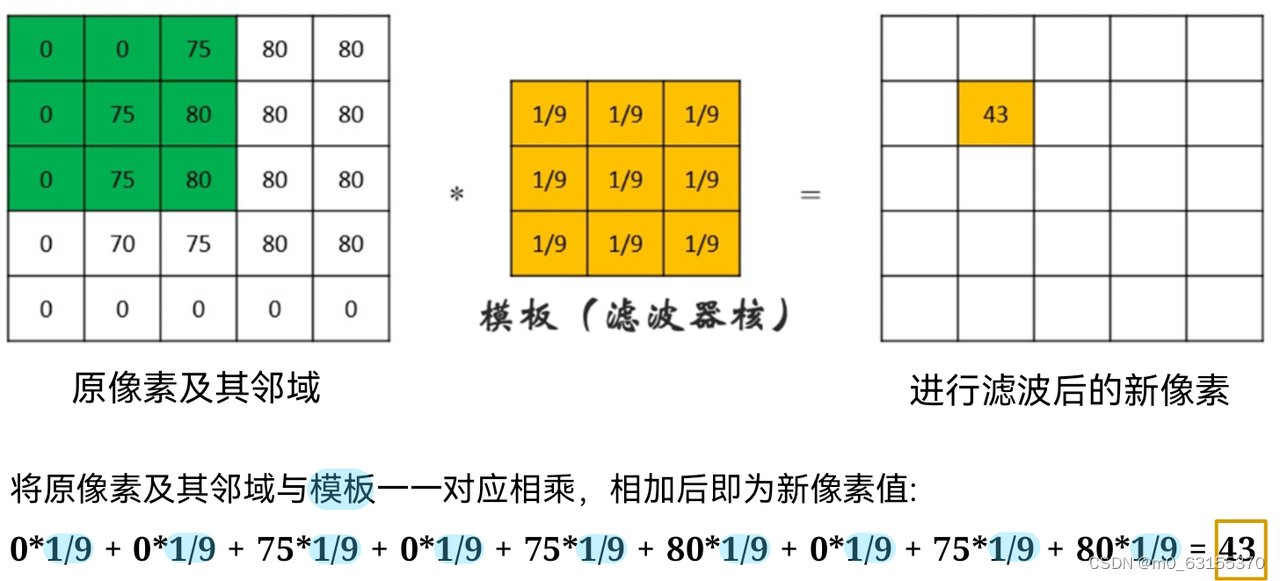
# 1. 滤波理论基础**

滤波是一种处理信号或图像的技术，用于去除不需要的噪声或干扰，同时保留有价值的信息。滤波器是一个数学函数或电路，可以根据特定的频率范围选择性地允许或抑制信号成分。

在滤波理论中，频率域和时域是两个重要的概念。频率域表示信号的频率成分，而时域表示信号随时间变化。滤波器可以通过在频率域或时域中选择性地修改信号的频谱来实现。

# 2.1 滤波器类型和特性

### 2.1.1 低通滤波器

低通滤波器允许低频信号通过，同时衰减高频信号。它们通常用于去除信号中的噪声和干扰，因为噪声通常具有较高的频率。

**特性：**

- 通带：0 Hz 到截止频率
- 阻带：截止频率以上
- 截止频率：低通滤波器允许通过的最大频率

### 2.1.2 高通滤波器

高通滤波器允许高频信号通过，同时衰减低频信号。它们通常用于提取信号中的高频成分，例如语音中的辅音。

**特性：**

- 通带：截止频率以上
- 阻带：0 Hz 到截止频率
- 截止频率：高通滤波器允许通过的最小频率

### 2.1.3 带通滤波器

带通滤波器允许特定频率范围内的信号通过，同时衰减其他频率。它们通常用于提取信号中的特定频段，例如音乐中的特定乐器。

**特性：**

- 通带：下截止频率到上截止频率
- 阻带：0 Hz 到下截止频率和上截止频率以上
- 下截止频率：带通滤波器允许通过的最低频率
- 上截止频率：带通滤波器允许通过的最高频率

### 2.1.4 带阻滤波器

带阻滤波器允许特定频率范围之外的信号通过，同时衰减该范围内的信号。它们通常用于去除信号中的特定频段，例如交流电源中的噪声。

**特性：**

- 通带：0 Hz 到下截止频率和上截止频率以上
- 阻带：下截止频率到上截止频率
- 下截止频率：带阻滤波器允许通过的最低频率
- 上截止频率：带阻滤波器允许通过的最高频率

# 3.1 MATLAB滤波器函数

MATLAB提供了多种滤波器函数，可用于实现各种滤波操作。这些函数包括：

- **filter()函数：**用于使用IIR（无限脉冲响应）或FIR（有限脉冲响应）滤波器对数据进行滤波。
- **filtfilt()函数：**用于使用IIR或FIR滤波器对数据进行零相位滤波。
- **conv()函数：**用于使用FIR滤波器对数据进行卷积。

#### 3.1.1 filter()函数

`filter()`函数的语法如下：

y = filter(B, A, x)

其中：

- `B`：滤波器的分子多项式系数向量。
- `A`：滤波器的分母多项式系数向量。
- `x`：输入数据序列。
- `y`：输出滤波后的数据序列。

#### 3.1.2 filtfilt()函数

`filtfilt()`函数的语法如下：

y = filtfilt(B, A, x)

其中：

- `B`：滤波器的分子多项式系数向量。
- `A`：滤波器的分母多项式系数向量。
- `x`：输入数据序列。
- `y`：输出滤波后的数据序列。

`filtfilt()`函数与`filter()`函数的区别在