MATLAB滤波器实战指南：一步步构建定制滤波器，解决实际问题

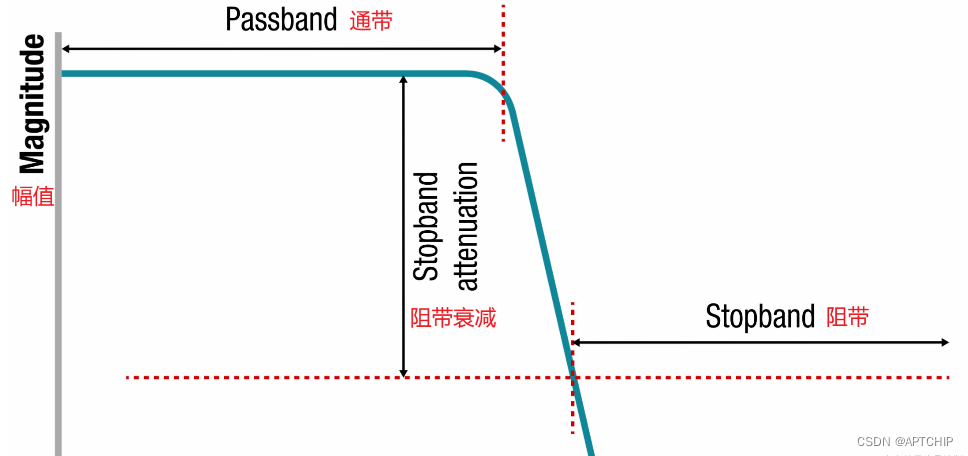
# 1. MATLAB滤波器基础

MATLAB滤波器是用于处理和分析信号的强大工具。它们可以用于从信号中去除噪声、提取特征和增强图像。MATLAB提供了一系列内置滤波器函数，使滤波器设计和应用变得容易。

本章介绍MATLAB滤波器的基础知识，包括滤波器的类型、特性和设计方法。它还提供了使用MATLAB工具箱设计和应用滤波器的分步指南。

# 2. 滤波器设计理论

### 2.1 数字滤波器类型及其特性

数字滤波器根据其特性和实现方式可分为以下几类：

- **有限脉冲响应 (FIR) 滤波器：** FIR 滤波器的输出仅取决于当前和过去的输入，其脉冲响应为有限长度。FIR 滤波器具有线性相位响应和良好的稳定性。
- **无限脉冲响应 (IIR) 滤波器：** IIR 滤波器的输出不仅取决于当前和过去的输入，还取决于过去的输出。IIR 滤波器的脉冲响应为无限长度，其相位响应是非线性的。IIR 滤波器可以实现更陡峭的截止频率，但其稳定性不如 FIR 滤波器。
- **自适应滤波器：** 自适应滤波器可以根据输入信号的统计特性自动调整其滤波器系数，以优化滤波性能。自适应滤波器常用于信号处理和控制系统中。
- **非线性滤波器：** 非线性滤波器使用非线性函数对输入信号进行处理。非线性滤波器可以实现更复杂的滤波操作，但其分析和设计更为复杂。

### 2.2 滤波器设计方法

滤波器设计方法主要分为以下几类：

#### 2.2.1 窗函数法

窗函数法是一种简单且常用的滤波器设计方法。该方法通过将理想滤波器的频域响应与一个窗函数相乘来设计实际滤波器。窗函数的形状和大小决定了滤波器的特性，如截止频率、通带和阻带衰减等。

**代码块：**

% 设计一个低通滤波器
order = 10; % 滤波器阶数
cutoff_freq = 0.2; % 截止频率
window = 'hamming'; % 窗函数类型

% 使用窗函数法设计滤波器
[b, a] = fir1(order, cutoff_freq, window);

% 绘制滤波器频率响应
freqz(b, a);

**逻辑分析：**

* `fir1` 函数使用窗函数法设计 FIR 滤波器。
* `order` 参数指定滤波器阶数，`cutoff_freq` 参数指定截止频率，`window` 参数指定窗函数类型。
* `freqz` 函数绘制滤波器的频率响应，可以观察滤波器的通带、阻带和相位响应。

#### 2.2.2 最小二乘法

最小二乘法是一种优化方法，用于设计滤波器以最小化其与理想滤波器的误差。该方法通过迭代调整滤波器系数来最小化误差函数。

**代码块：**

% 设计一个带通滤波器
order = 10; % 滤波器阶数
passband_freq = [0.2, 0.4]; % 通带频率
stopband_freq = [0.1, 0.5]; % 阻带频率

% 使用最小二乘法设计滤波器
[b, a] = firls(order, passband_freq, stopband_freq);

% 绘制滤波器频率响应
freqz(b, a);

**逻辑分析：**

* `firls` 函数使用最小二乘法设计 FIR 滤波器。
* `order` 参数指定滤波器阶数，`passband_freq` 和 `stopband_freq` 参数指定通带和阻带频率。
* `freqz` 函数绘制滤波器的频率响应，可以观察滤波器的通带、阻带和相位响应。

#### 2.2.3 迭代法

迭代法是一种通过迭代更新滤波器系数来设计滤波器的方法。该方法从一个初始滤波器开始，并通过反复应用优化算法来逐渐改善滤波器的性能。

**代码块：**

% 设计一个高通滤波器
order = 10; % 滤波器阶数
cutoff_freq = 0.2; % 截止频率

% 使用迭代法设计滤波器
[b, a] = iirnotch(cutoff_freq, order);

% 绘制滤波器频率响应
freqz(b, a);

**逻辑分析：**

* `iirnotch` 函数使用迭代法设计 IIR 滤波器。
* `order` 参数指定滤波器阶数，`cutoff_freq` 参数指定截止频率。
* `freqz` 函数绘制滤波器的频率响应，可以观察滤波器的通带、阻带和相位响应。

**表格：滤波器设计方法比较**

| 方法 | 优点 | 缺点 |
|---|---|---|
| 窗函数法 | 简单易用 | 频率响应存在纹波 |
| 最小二乘法 | 优化误差 | 计算量大 |
| 迭代法 | 可以实现复杂滤波器 | 迭代过程可能收敛缓慢