MapReduce中的排序技术：基础到高级应用的完整指南

# 1. MapReduce排序技术概述

在处理大规模数据集时，MapReduce排序技术是大数据处理的基石。MapReduce框架通过提供可扩展的并行处理能力，实现对海量数据的高效排序。本章节将简要介绍MapReduce排序技术的基本概念、发展历程以及它在数据处理中的核心地位。我们将概述排序在MapReduce中的作用，以及为什么它是分布式计算环境中不可或缺的一部分。通过了解排序技术，数据科学家和工程师能够更好地理解如何利用MapReduce框架优化数据处理流程。

# 2. MapReduce排序机制的理论基础

## 2.1 MapReduce框架的工作原理

### 2.1.1 Map阶段与Reduce阶段的流程

MapReduce框架的设计初衷是为了简化大规模数据集的并行运算。其核心思想是将复杂的并行计算问题分解成两个主要阶段：Map阶段和Reduce阶段。

在Map阶段，框架将输入数据集拆分为固定大小的块（split），然后并行地执行用户定义的Map函数。Map函数对每个块独立进行处理，输出一系列键值对（key-value pairs）。这个过程通常包含数据过滤和数据转换的逻辑。

// 示例：Map函数的伪代码
map(String key, String value):
    // key: document name
    // value: document contents
    for each word w in value:
        EmitIntermediate(w, "1");

Map函数输出的键值对会被送到Reduce阶段。在Reduce阶段，所有的键值对首先根据键（key）进行排序和分组。然后，框架对每个唯一的键调用Reduce函数，Reduce函数再对分组后的值集合进行处理，最终输出结果。

// 示例：Reduce函数的伪代码
reduce(String key, Iterator values):
    // key: a word
    // values: a list of counts
    int result = 0;
    for each v in values:
        result += ParseInt(v);
    Emit(key, String.valueOf(result));

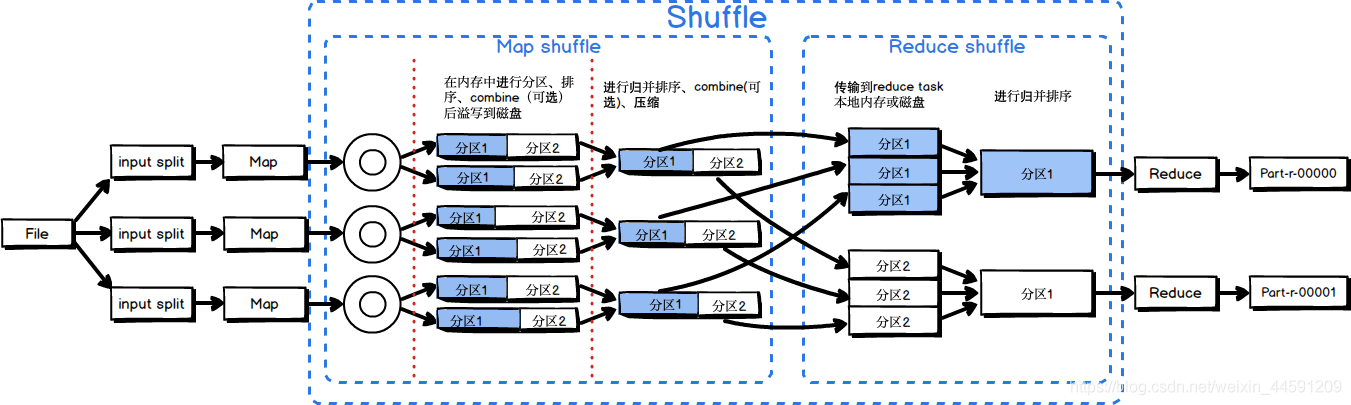
### 2.1.2 Shuffle过程的排序机制

Shuffle过程是MapReduce框架中连接Map和Reduce阶段的关键步骤。在这个过程中，数据从Map任务传输到Reduce任务。Shuffle的排序机制确保了在Reduce阶段中，相同的键值对会被发送到同一个Reduce任务。

Shuffle过程可划分为以下几个步骤：

1. **分区（Partitioning）**：框架根据Map输出的键和预定义的分区函数决定哪个Reduce任务接收键值对。
2. **排序（Sorting）**：在每个Map任务完成之后，系统会对输出的键值对进行排序。排序通常基于键（key）进行，保证相同键的键值对聚集在一起。
3. **合并（Combining）**：在某些情况下，MapReduce框架会进行一个预合并（Combiner）操作，这个过程在Map端进行，合并相同键的值，减少网络传输的数据量。
4. **传输（Transfer）**：排序后的键值对被发送到相应的Reduce任务。这一过程涉及到大量的数据传输，可能会受到网络带宽的限制。
5. **再排序（Secondary Sorting）**：在Reduce任务中，会再次对来自不同Map任务的键值对进行排序，确保整个数据集的顺序一致性。

## 2.2 MapReduce排序与分布式计算

### 2.2.1 排序对数据处理的影响

排序是MapReduce中一个核心的概念，它影响着数据处理的方式和效率。在分布式计算环境中，排序不仅可以帮助决定数据如何在各个节点之间分布，而且还能决定数据的组织方式，从而提高后续处理的效率。

排序使得：

- 数据可以根据键的顺序进行高效检索。
- 在某些情况下，能够实现有效的压缩，因为有序数据可以使用更加高效的压缩算法。
- 通过分组键值对，可以并行执行多个任务，减少处理时间。
- 帮助实现去重操作，因为重复的键值对在排序后会聚集在一起。

### 2.2.2 分布式排序的挑战与策略

分布式排序面临着数据倾斜和网络带宽等挑战。数据倾斜是指数据在不同节点间分布不均匀，导致某些节点任务过重，而其他节点空闲。网络带宽的限制则涉及到数据传输效率的问题，尤其是当需要传输大量已排序的数据时。

为了解决这些问题，可以采取以下策略：

- **分区策略**：通过合理设计分区函数，确保数据均匀分布。
- **采样技术**：在Map任务开始之前，对输入数据进行采样，分析其分布特性，据此来优化分区策略。
- **预排序与采样**：在Map任务中进行预排序，然后利用采样的结果来避免网络传输中的数据倾斜。
- **网络流量控制**：优化数据传输的优先级和顺序，减少网络拥塞。

## 2.3 排序相关的性能考量

### 2.3.1 内存与磁盘排序的对比

MapReduce排序过程中可能会涉及到内存排序和磁盘排序。内存排序是指Map或Reduce任务在内存中完成排序，而磁盘排序则需要借助于磁盘存储空间。

内存排序的优点是速度快，但缺点是受限于可用内存大小。磁盘排序虽然速度较慢，但可以处理比内存大得多的数据集。

### 2.3.2 网络带宽对排序的影响

在MapReduce框架中，排序和Shuffle过程会涉及到大量的数据在网络中传输。网络带宽成为了一个重要的性能瓶颈。提升带宽可以减少数据传输时间，从而提高整体任务的执行速度。因此，在设计MapReduce作业时，应该充分考虑到网络带宽的限制，并尽可能地优化数据传输过程。

# 3. MapReduce排序技术实践

## 3.1 排序技术的编程实践

### 3.1.1 自定义排序的实现

自定义排序在MapReduce中是一个强大的特性，允许开发者根据自己的需求定义对象排序的规则。在Hadoop的MapReduce框架中，实现自定义排序通常需要自定义`WritableComparable`接口，该接口继承了`Writable`和`Comparable`接口。

一个典型的`WritableComparable`实现包含两个关键方法：`write(DataOutput out)`和`readFields(DataInput in)`，分别用于序列化和反序列化数据。除此之外，还需要覆盖`compareTo`方法来定义排序逻辑。

下面是一个简单的自定义`WritableComparable`实现的例子：

import org.apache.hadoop.io.*;

public class MyWritable implements WritableComparable<MyWritable> {
    private IntWritable first;
    private LongWritable second;

    public MyWritable() {
        first = new IntWritable();
        second = new LongWritable();
    }

    @Override
    public void write(DataOutput out) throws IOException {
        first.write(out);
        second.write(out);
    }

    @Override
    public void readFields(DataInput in) throws IOException {
        first.readFields(in);
        second.readFields(in);
    }

    @Override
    public int compareTo(MyWritable o) {
        int cmp = ***pareTo(o.first);
        if (cmp != 0) {
            return cmp;
        }
        ***pareTo(o.second);
    }
    // Getters and setters for first and second
    // ...
}

在上述代码中，`compareTo`方法首先比较`IntWritable`类型的`first`字段，如果它们相等，则比较`LongWritable`类型的`second`字段。这种比较逻辑是自定义排序规则的关键。

### 3.1.2 排序键的设计

选择合适的排序键是优化MapReduce作业性能的重要方面。排序键不仅决定了数据在Map阶段的排序方式，也影响着Shuffle阶段和Reduce阶段的数据传输效率。

设计排序键时需要考虑以下因素：

- **键的唯一性**：确保每个键是唯一的，这有助于避免数据丢失或重复处理。
- **键的频率**：高频键可能会导致数据倾斜，因此要考虑引入随机前缀或使用组合键来平衡负载。
- **排序顺序**：数据的自然排序顺序可能会影响MapReduce作业的性能。例如，如果频繁进行范围查询，那么连续键的顺序很重要。

例如，在一个日志分析的MapReduce作业中，如果以时间为排序键，那么频繁查询某一个时间段的日志将非常高效，因为连续时间的数据在Map阶段会聚集在一起。

### 3.2 高级排序技巧

#### 3.2.1 多级排序的实现

在某些复杂的场景下，单个排序键可能无法满足需求，这时就需要使用多级排序（Composite Sorting）。多级排序可以先按照一个键排序，然后在相同键值的集合中再按照另一个键排序。

例如，考虑一个需要按照部门和姓名进行排序的场景。可以先按部门排序，然后在每个部门内部按姓名排序。

实现多级排序的代码可能如下所示：

public int compareTo(MyWritable o) {
    int result = ***pareTo(o.first);
    if (result == 0) {
        result = ***pareTo(o.second);
    }
    return result;
}

在这个比较方法中，首先比较`first`字段，如果相同，则比较`second`字段。

#### 3.2.2 自定义比较器的使用

在某些情况下，内置的比较器可能不足以满足复杂的排序需求。这时，可以使用自定义比较器来实现更灵活的排序逻辑。

自定义比较器需要实