真值表分析：从简单到复杂，深入探索逻辑运算（10个实战案例）

# 1. 真值表的概念和基本运算**

真值表是一种表格，它显示了逻辑运算符在所有可能的输入组合下的输出值。在真值表中，输入值通常用布尔变量表示，布尔变量只能取两个值：真 (True) 或假 (False)。

基本逻辑运算符包括：
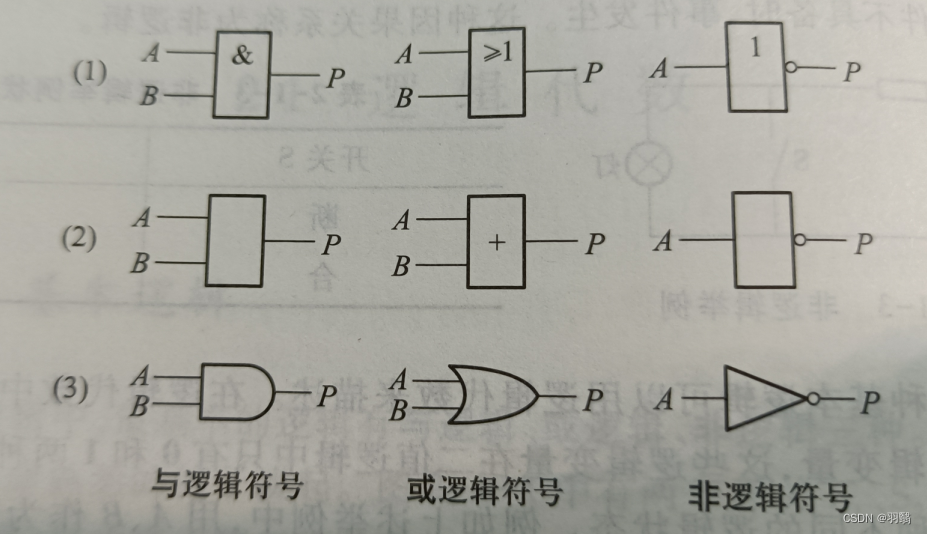
- 与运算 (AND)：当且仅当所有输入都为真时，输出才为真。
- 或运算 (OR)：当至少一个输入为真时，输出为真。
- 非运算 (NOT)：输入为真时，输出为假；输入为假时，输出为真。

# 2.1 布尔代数定理及其应用

### 2.1.1 同一律、矛盾律和排除中律

布尔代数中，同一律、矛盾律和排除中律是三个基本定理，它们定义了逻辑运算的基本性质。

**同一律：**

A ∨ A = A
A ∧ A = A

**解释：** 任何逻辑变量与其自身进行逻辑或或逻辑与运算，结果始终等于自身。

**矛盾律：**

A ∨ ¬A = 1
A ∧ ¬A = 0

**解释：** 任何逻辑变量与其否定进行逻辑或运算，结果始终为真；与其否定进行逻辑与运算，结果始终为假。

**排除中律：**

¬(¬A) = A

**解释：** 对任何逻辑变量进行两次否定，结果始终等于自身。

### 2.1.2 分配律、结合律和交换律

分配律、结合律和交换律是布尔代数中的其他三个重要定理，它们定义了逻辑运算之间的关系。

**分配律：**

A ∨ (B ∧ C) = (A ∨ B) ∧ (A ∨ C)
A ∧ (B ∨ C) = (A ∧ B) ∨ (A ∧ C)

**解释：** 逻辑或运算对逻辑与运算具有分配性，逻辑与运算对逻辑或运算也具有分配性。

**结合律：**

(A ∨ B) ∨ C = A ∨ (B ∨ C)
(A ∧ B) ∧ C = A ∧ (B ∧ C)

**解释：** 逻辑或运算和逻辑与运算都具有结合性，即多个运算可以任意组合。

**交换律：**

A ∨ B = B ∨ A
A ∧ B = B ∧ A

**解释：** 逻辑或运算和逻辑与运算都具有交换性，即运算顺序可以互换。

### 应用

布尔代数定理在逻辑运算中有着广泛的应用，例如：

* **电路设计：** 布尔代数定理用于设计和简化逻辑电路。
* **计算机编程：** 布尔代数定理用于编写逻辑判断和控制语句。
* **数学证明：** 布尔代数定理用于证明逻辑命题和定理。
* **人工智能：** 布尔代数定理用于表示和推理知识。

# 3.1 数字电路设计中的真值表

**3.1.1 组合逻辑电路的真值表**

组合逻辑电路是一种输出仅取决于其当前输入的逻辑电路。其真值表描述了电路输出在所有可能输入组合下的值。例如，一个简单的与门电路具有两个输入 A 和 B，其真值表如下：

| A | B | 输出 |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |

从真值表中可以看出，只有当 A 和 B 都为 1 时，与门输出才为 1。

**3.1.2 时序逻辑电路的真值表**

时序逻辑电路的输出不仅取决于其当前输入，还取决于其过去的状态。其真值表描述了电路输出在所有可能输入和状态组合下的值。例如，一个简单的 D 触发器电路具有一个输入 D 和一个时钟输入 CLK，其真值表如下：

| 当前状态 | CLK | D | 下一个状态 | 输出 |
|---|---|---|---|---|
| 0 | 0 | X | 0 | 0 |
| 0 | 1 | 0 | 0 | 0 |
| 0 | 1 | 1 | 1 | 1 |
| 1 | 0 | X | 1 | 1 |
| 1 | 1 | 0 | 0 | 0 |
| 1 | 1 | 1 | 1 | 1 |

从真值表中可以看出，D 触发器的输出不仅取决于 D 输入，还取决于其当前状态。当 CLK 为上升沿时，D 输入的值将