揭秘真值表：逻辑运算的幕后黑手，助你轻松理解

# 1. 逻辑运算的基础**

逻辑运算是一种对逻辑命题进行操作的方法，用于确定命题的真假性。逻辑运算符是执行这些操作的符号，它们将一个或多个输入值（称为操作数）转换为一个输出值（称为结果）。

常见的逻辑运算符包括：

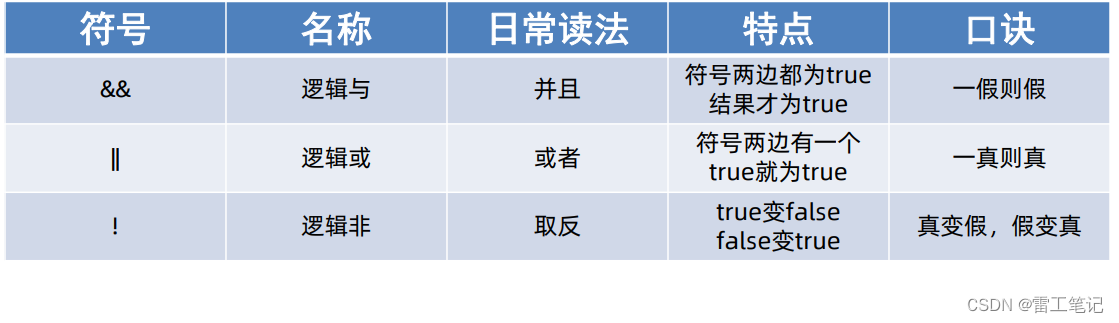
* 逻辑与 (AND)
* 逻辑或 (OR)
* 逻辑非 (NOT)
* 逻辑异或 (XOR)

# 2. 真值表：逻辑运算的指南

### 2.1 真值表的概念和结构

**2.1.1 真值表的组成元素**

真值表是一个表格，用于显示逻辑运算符在所有可能的输入组合下的输出结果。它由以下元素组成：

- **输入列：**列出所有可能的输入组合。对于 n 个输入变量，共有 2^n 个可能的输入组合。
- **输出列：**显示逻辑运算符在每个输入组合下的输出结果。
- **运算符符号：**位于真值表顶部，表示所考虑的逻辑运算符。

**2.1.2 真值表的解读方式**

要解读真值表，请按照以下步骤操作：

1. 确定输入列中要评估的特定输入组合。
2. 找到与该输入组合对应的输出列。
3. 输出列中的值表示逻辑运算符在该输入组合下的输出结果。

### 2.2 逻辑运算符的真值表

**2.2.1 逻辑与 (AND)**

| A | B | A AND B |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |

**逻辑分析：**AND 运算符仅当两个输入都为真时才输出真。

**2.2.2 逻辑或 (OR)**

| A | B | A OR B |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |

**逻辑分析：**OR 运算符当至少一个输入为真时输出真。

**2.2.3 逻辑非 (NOT)**

| A | NOT A |
|---|---|
| 0 | 1 |
| 1 | 0 |

**逻辑分析：**NOT 运算符将输入取反，即 0 变为 1，1 变为 0。

**2.2.4 逻辑异或 (XOR)**

| A | B | A XOR B |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |

**逻辑分析：**XOR 运算符仅当两个输入不同时才输出真。

# 3.1 逻辑表达式的求值

**3.1.1 使用真值表求值逻辑表达式**

使用真值表求值逻辑表达式是一个简单而有效的过程。对于一个给定的逻辑表达式，我们可以创建一个真值表，其中包含所有可能的输入变量组合及其相应的输出值。通过检查真值表，我们可以确定逻辑表达式的真值。

例如，考虑以下逻辑表达式：

(A AND B) OR (NOT C)

为了求值此表达式，我们可以创建一个真值表，其中包含所有可能的 A、B 和 C 的组合：

| A | B | C | (A AND B) | (NOT C) | (A AND B) OR (NOT C) |
|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 1 | 1 |
| 0 | 0 | 1 | 0 | 0 | 0 |
| 0 | 1 | 0 | 0 | 1 | 1 |
| 0 | 1 | 1 | 0 | 0 | 0 |
| 1 | 0 | 0 | 0 | 1 | 1 |
| 1 | 0 | 1 | 0 | 0 | 0 |
| 1 | 1 | 0 | 1 | 1 | 1 |
| 1 | 1 | 1 | 1 | 0 | 1 |

通过检查真值表，我们可以看到逻辑表达式 (A AND B) OR (NOT C) 在以下情况下为真：

* 当 A 和 B 都为真时
* 当 C 为假时

**3.1.2 逻辑表达式的化简**

真值表还可以用于化简逻辑表达式。化简是指将逻辑表达式转换为等效但更简单的形式。通过使用真值表，我们可以识别和消除冗余项，从而获得更简洁的表达式。

例如，考虑以下逻辑表达式：

(A AND B) OR (A AND NOT B)

我们可以创建一个真值表来化简此表达式：

| A | B | (A AND B) | (A AND NOT B) | (A AND B) OR (A AND NOT B) |
|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 |
| 0 | 1 | 0 | 0 | 0 |
| 1 | 0 | 0 | 0 | 0 |
| 1 | 1 | 1 | 0 | 1 |

通过检查真值表，我们可以看到 (A AND B) OR (A AND NOT B) 在所有情况下都与 A 相等。因此，我们可以将表达式化简为：

(A AND B) OR (A AND NOT B) = A

# 4. 真值表的扩展应用

### 4.1 布尔代数与真值表

#### 4.1.1 布尔代数的基本定理

布尔代数是一套定义在布尔值（真和假）上的代数系统。它由以下基本定理组成：

- **交换律：** A AND B = B AND A，A OR B = B OR A
- **结合律：** (A AND B) AND C = A AND (B AND C)，(A OR B) OR C = A OR (B OR C)
- **分配律：** A AND (B OR C) = (A AND B) OR (A AND C)，A OR (B AND C) = (A OR B) AND (A OR C)
- **吸收律：** A AND (A OR B) = A，A OR (A AND B) = A
- **单位元：** A AND TRUE = A，A OR FALSE = A
- **零元：** A AND FALSE = FALSE，A OR TRUE = TRUE
- **德摩根定理：** NOT (A AND B) = NOT A OR NOT B，NOT (A OR B) = NOT A AND NOT B

#### 4.1.2 真值表在布尔代数中的应用

真值表可以用来验证布尔代数定理。例如，要验证交换律，我们可以构造一个真值表，其中包含 A、B 和 A AND B 的所有可能值：

| A | B | A AND B |
|---|---|---|
| T | T | T |
| T | F | F |
| F | T | F |
| F | F | F |

从真值表中，我们可以看到 A AND B 的值与 B AND A 的值相同，这验证了交换律。

### 4.2 计算机科学中的真值表

#### 4.2.1 真值表在计算机编程中的作用

真值表在计算机编程中广泛用于：

- **条件语句：** 真值表可以用来确定条件语句的执行流。例如，以下 Python 代码使用真值表来确定是否打印消息：

a = True
b = False

if a and b:
    print("消息")

- **布尔表达式：** 真值表可以用来求解布尔表达式的值。例如，以下真值表显示了 A OR B 表达式的值：

| A | B | A OR B |
|---|---|---|
| T | T | T |
| T | F | T |
| F | T | T |
| F | F | F |

#### 4.2.2 真值表在算法设计中的应用

真值表可以用来：

- **设计算法：** 真值表可以用来设计算法，以确定特定条件下应执行的操作。例如，以下真值表显示了确定最大值的算法：

| A | B | 最大值 |
|---|---|---|
| T | T | A |
| T | F | A |
| F | T | B |
| F | F | B |

- **优化算法：** 真值表可以用来优化算法，以减少执行时间和资源消耗。例如，通过使用真值表，我们可以确定哪些条件是冗余的，并从算法中删除它们。

# 5. 真值表的局限性和挑战

### 5.1 真值表不能处理模糊逻辑

真值表是基于二值逻辑的，即只有真和假两个值。然而，在现实世界中，许多问题都具有模糊性，无法用真或假来明确表示。例如，一个人的健康状况可能是“健康”、“亚健康”或“不健康”，而真值表无法处理这种模糊性。

### 5.2 真值表在复杂逻辑系统中的应用挑战

随着逻辑系统的复杂性增加，真值表的大小和复杂性也会呈指数级增长。对于具有大量输入变量的复杂逻辑系统，真值表可能变得难以管理和分析。例如，一个具有 10 个输入变量的逻辑系统将需要一个包含 2^10 = 1024 行的真值表。

### 5.3 替代真值表的其他方法

为了解决真值表的局限性，已经提出了替代方法来处理模糊逻辑和复杂逻辑系统。这些方法包括：

- **模糊逻辑：**模糊逻辑使用模糊集来表示模糊概念，允许在真和假之间有不同的程度。
- **贝叶斯网络：**贝叶斯网络是一种概率图模型，它使用概率来表示事件之间的关系，可以处理不确定性和模糊性。
- **神经网络：**神经网络是一种机器学习模型，可以学习复杂函数并处理非线性关系，包括模糊逻辑。