真值表与布尔代数：逻辑运算的数学桥梁（深入解读）

# 1. 真值表与布尔代数的基础**

真值表是一种逻辑工具，用于表示逻辑运算的结果。它是一个表格，其中每一行代表一组输入值，每一列代表一个逻辑运算的结果。真值表可以帮助我们理解逻辑运算的性质和关系。

布尔代数是一种数学系统，用于表示和操作逻辑值。它由布尔运算（如与、或、非）和布尔定理（如吸收律、结合律）组成。布尔代数为真值表的分析和操作提供了理论基础。

通过使用真值表和布尔代数，我们可以分析和设计逻辑电路，优化布尔表达式，并解决计算机科学中的各种问题。

# 2. 布尔代数的运算和定理

### 2.1 布尔运算的定义和性质

#### 2.1.1 与、或、非运算

布尔运算是一种二元运算，即它作用于两个布尔值（真或假），并产生一个布尔值作为结果。最基本的布尔运算有：

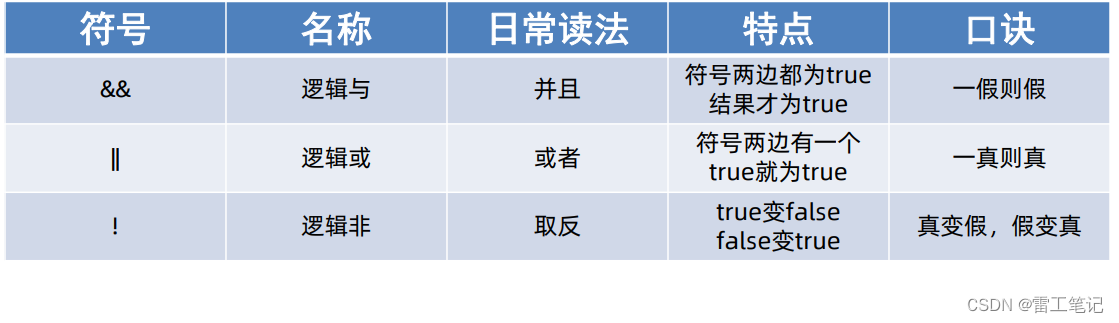
- **与（AND）运算：** 两个布尔值都为真时，结果为真；否则为假。
- **或（OR）运算：** 两个布尔值中至少有一个为真时，结果为真；否则为假。
- **非（NOT）运算：** 将布尔值取反，即真变假，假变真。

#### 2.1.2 异或、蕴涵、等价运算

除了基本运算外，还有其他一些布尔运算：

- **异或（XOR）运算：** 两个布尔值不同时，结果为真；否则为假。
- **蕴涵（IMPLICATION）运算：** 当第一个布尔值为真时，第二个布尔值为真或假，结果为真；否则为假。
- **等价（EQUIVALENCE）运算：** 两个布尔值相同时，结果为真；否则为假。

### 2.2 布尔代数的定理

布尔代数是一套公理化的系统，用于操作布尔值。它定义了一组定理，这些定理可以用来化简和操作布尔表达式。

#### 2.2.1 吸收律、结合律、分配律

- **吸收律：** A + AB = A，A * (A + B) = A
- **结合律：** (A + B) + C = A + (B + C)，(A * B) * C = A * (B * C)
- **分配律：** A * (B + C) = A * B + A * C，A + (B * C) = (A + B) * (A + C)

#### 2.2.2 德·摩根定理、对偶律

- **德·摩根定理：** ¬(A + B) = ¬A * ¬B，¬(A * B) = ¬A + ¬B
- **对偶律：** A + B = ¬(¬A * ¬B)，A * B = ¬(¬A + ¬B)

**代码块：**

# 与运算
a = True
b = False
result = a and b
print(result)  # 输出：False

# 或运算
a = True
b = False
result = a or b
print(result)  # 输出：True

# 非运算
a = True
result = not a
print(result)  # 输出：False

**逻辑分析：**

* 与运算：如果两个布尔值都为真，则结果为真；否则为假。
* 或运算：如果两个布尔值中至少有一个为真，则结果为真；否则为假。
* 非运算：将布尔值取反，即真变假，假变真。

**参数说明：**

* `a`