利用01背包问题动态规划进行组合优化解决

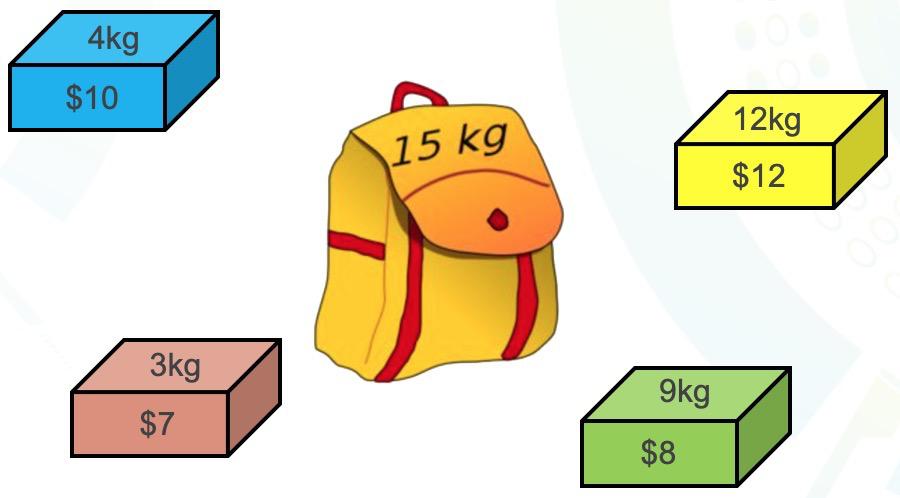
# 1. 组合优化问题简介

组合优化问题是指在一组可能的解中寻找最优解的问题，通常涉及多个变量之间的组合关系。这类问题在实际生活中有着广泛的应用，如物流路径规划、资源分配、生产排程等领域。

在组合优化问题中，我们需要在众多可能的组合方案中找到最优解，这往往需要耗费大量的时间和资源。因此，设计高效的算法来解决这些问题至关重要。

通过动态规划算法，可以有效地解决组合优化问题，通过分阶段地决策并利用子问题的最优解来求解整体的最优解。动态规划在解决组合优化问题中具有重要的作用，能够提高问题求解的效率和准确度。在接下来的章节中，将深入探讨动态规划算法在组合优化问题中的应用和具体求解方法。

# 2. 动态规划算法概述

### 2.1 动态规划的基本概念

动态规划（Dynamic Programming，简称 DP）是一种解决多阶段决策过程最优化问题的数学方法。其基本思想是将原问题分解为若干个子问题，通过已知子问题的最优解推导出原问题的最优解。在求解动态规划问题时，需要满足最优子结构和重叠子问题两个条件。

### 2.2 动态规划的核心思想

动态规划的核心思想是递推和存储。通过建立状态转移方程，将问题划分为子问题，然后依次解决子问题直至解决原问题。在求解过程中，需要合理设计状态表示和状态转移方程，同时利用数组或其他数据结构存储中间结果，避免重复计算，提高效率。

#### 动态规划的主要特点：
- 求解的问题可以分解为若干个子问题；
- 子问题之间存在重叠，即同一个子问题可能会被多次求解；
- 通过存储子问题的解来避免重复计算，提高效率；
- 动态规划适用于多阶段决策最优化问题，能够找到全局最优解。

#### 动态规划的应用领域：
- 背包问题（01背包、完全背包、多重背包）
- 图论问题（最短路径、最大流）
- 字符串处理（最长公共子序列、编辑距离）
- 数值问题（Fibonacci数列、最大子数组和）
- 游戏策略（博弈问题、动态规划算法）

### 2.3 动态规划的经典问题分析

在动态规划中，常见的经典问题包括背包问题、最长递增子序列等。这些问题通过合理的状态定义和状态转移方程，可以运用动