01背包问题在路径规划中的应用探究

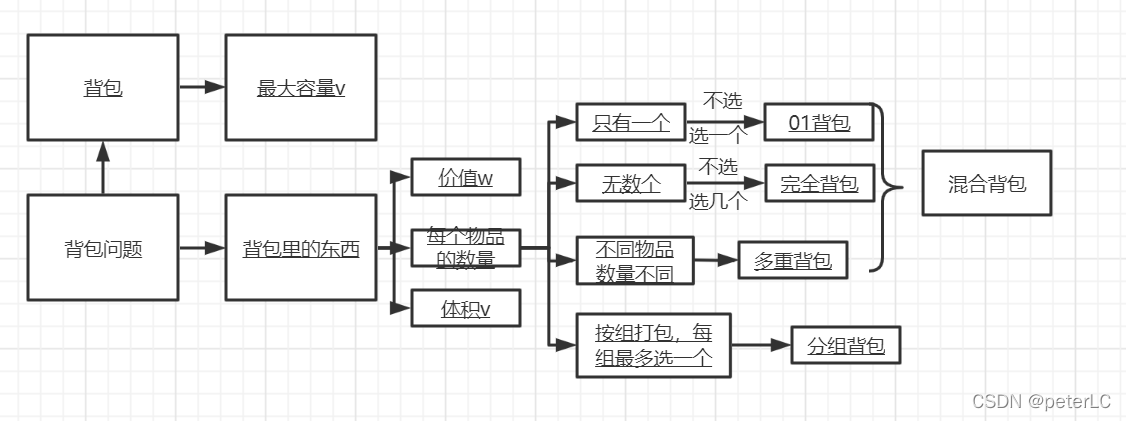
# 1.1 背包问题的定义与分类

背包问题是一个经典的组合优化问题，其基本思想是，在有限的资源约束下，如何选择物品放入背包，使得价值最大化。根据不同的约束条件和限制性质，背包问题可分为多种类型，常见的有0/1背包问题、分数背包问题和多重背包问题。0/1背包问题要求每种物品只能选择一次，分数背包问题可选取物品的一部分，而多重背包问题允许多次选择同一种物品。不同类型的背包问题在实际应用中有着各自的特点和解法，对于计算机科学领域的算法设计与优化起着重要的作用。

# 2. 路径规划与动态规划

### 2.1 动态规划在路径规划中的作用
在路径规划中，动态规划是一种重要的算法思想，能够有效地解决各种最优路径或最短路径的计算问题。通过动态规划，我们可以找到从起点到终点的最优路径，实现路径规划的精准性和高效性。

#### 2.1.1 最短路径问题
最短路径问题是路径规划中常见的一种情况，我们希望找到两点之间经过的路径长度最短的路线。在动态规划中，有几种经典的算法可以解决最短路径问题，其中包括：

##### 2.1.1.1 Dijkstra算法
Dijkstra算法是一种用于求解图中某一节点到其余各节点的最短路径的算法。它采用贪心策略，通过逐步扩展离起始节点最近的节点来逐步确定最短路径。

# Python实现Dijkstra算法
def dijkstra(graph, start):
    dist = {node: float('infinity') for node in graph}
    dist[start] = 0
    queue = []
    heapq.heappush(queue, (dist[start], start))

    while queue:
        current_dist, current_node = heapq.heappop(queue)

        if current_dist > dist[current_node]:
            continue

        for neighbor, weight in graph[current_node].items():
            distance = current_dist + weight
            if distance < dist[neighbor]:
                dist[neighbor] = distance
                heapq.heappush(queue, (distance, neighbor))
    return dist

##### 2.1.1.2 Floyd算法
Floyd算法是一种动态规划算法，用于解决任意两点之间的最短路径问题。该算法通过中转点逐步优化路径长度，直到得到最优解。

# Python实现Floyd算法
def floyd(graph):
    n = len(graph)
    for k in range(n):
        for i in range(n):
            for j in range(n):
                graph[i][j] = min(graph[i][j], graph[i][k] + graph[k][j])
    return graph

#### 2.1.2 最优路径规划
除了最短路径问题，最优路径规划也是路径规划中的关键问题之一。在最优路径规划中，我们不仅考虑路径的长度，还需要考虑其他因素，如代价、时间等。

##### 2.1.2.1 A*算法
A*算法是一种启发式搜索算法，用于在图中找到起点到终点的最佳路径。该算法综合考虑了路径的代价和启发式评估函数，能够高效地搜索最优路径。

# Python实现A*算法
def A_star(graph, start, end):
    open_list = [start]
    closed_list = []

    while open_list:
        current_node = min(open_list, key=lambda x: graph[x]['f'])
        open_list.remove(current_node)
        closed_list.append(current_node)

        if current_node == end:
            break

        for neighbor in graph[current_node]['neighbors']:
            if neighbor in closed_