如何优化01背包问题的动态规划解法

# 1. 01背包问题的基本概念

## 1.1 背包问题的定义

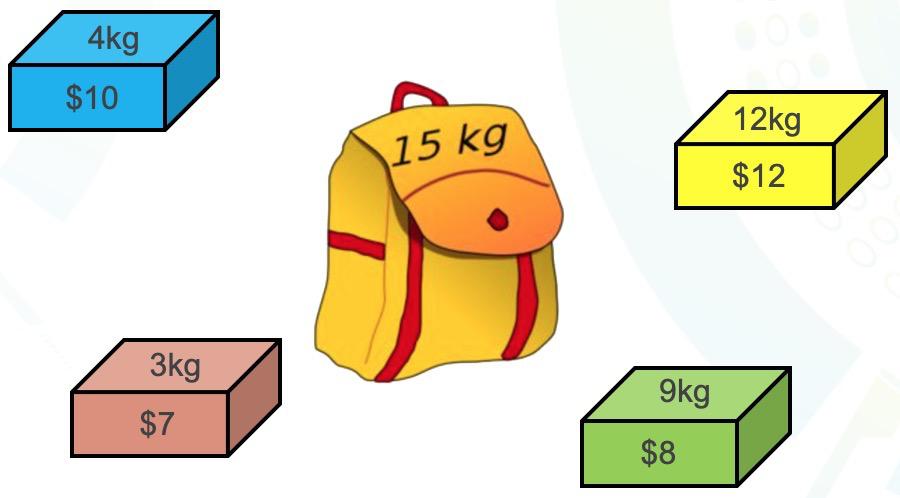
背包问题是一个经典的组合优化问题，在给定背包容量和一组物品的重量与价值的情况下，如何选择装入背包的物品以获取最大总价值的问题。其中，01背包问题指的是每种物品只能选择一次装入背包。

## 1.2 动态规划解法的基本原理

动态规划是解决背包问题的常用方法，通过拆分子问题，建立状态转移方程，利用之前求解过的子问题结果来求解更复杂的大问题，实现对背包问题的优化求解。

在动态规划解法中，需要定义状态数组来存储中间状态，通过填表的方式逐步求解最优解，从而得到背包问题的最优解。

# 2. 动态规划解法的实现步骤

在解决01背包问题时，动态规划是一个常用的方法。要实现动态规划解法，需要按照以下步骤进行：确定状态转移方程、初始化状态数组和边界条件，以及填表求解最优解。

### 2.1 确定状态转移方程

#### 2.1.1 状态的定义

在动态规划中，首先需要定义问题的状态。对于01背包问题，一个常见的状态定义是 dp[i][j]，表示在前i个物品中选择，在背包容量为j的情况下所能获得的最大价值。

#### 2.1.2 状态转移方程的推导

状态转移方程是动态规划问题的核心。对于01背包问题，状态转移方程可以表示为：

dp[i][j] = max(dp[i-1][j], dp[i-1][j-weight[i]] + value[i])

这里 dp[i][j] 表示将第i个物品放入背包时的最优解，可以选择将第i个物品放入背包或不放入背包两种情况，取其中价值较大的情况。

### 2.2 初始化状态数组和边界条件

在开始填表前，需要初始化状态数组和边界条件。对于01背包问题，可以初始化一个二维数组 dp，其中 dp[i][j] 初始值为0，表示没有物品放入背包时的初始状态。

### 2.3 填表求解最优解

接着按照状态转移方程填表，从前往后依次计算 dp[i][j] 的值，直至填满整个表格。最终 dp[n][W] 中存储的就是在前n个物品中做出选择，在背包容量为W的情况下所能获得的最大价值。

通过以上步骤，就可以使用动态规划方法解决01背包问题，找到最优解。

# 3. 优化01背包问题的动态规划解法

### 3.1 优化空间复杂度的方法

#### 3.1.1 滚动数组的应用

在动态规划过程中，我们可以通过滚动数组的技巧来优化空间复杂度。具体而言，如果在填表过程中只需要用到上一行的信息，我们可以只保留两行的状态数组，每次只更新这两行的值，而不需要保留完整的状态数组。这样做可以将空间复杂度从O(N * C)降低