使用01背包问题动态规划解决实际背包装填问题

# 1. 背包问题简介

### 1.1 什么是背包问题

背包问题是一个经典的组合优化问题，在计算机科学和数学领域被广泛研究和应用。其基本形式是：给定一个背包，它能容纳一定重量的物品，每个物品都有自己的价值和重量，目标是在不超过背包承重的情况下，使得背包内物品的总价值最大化。

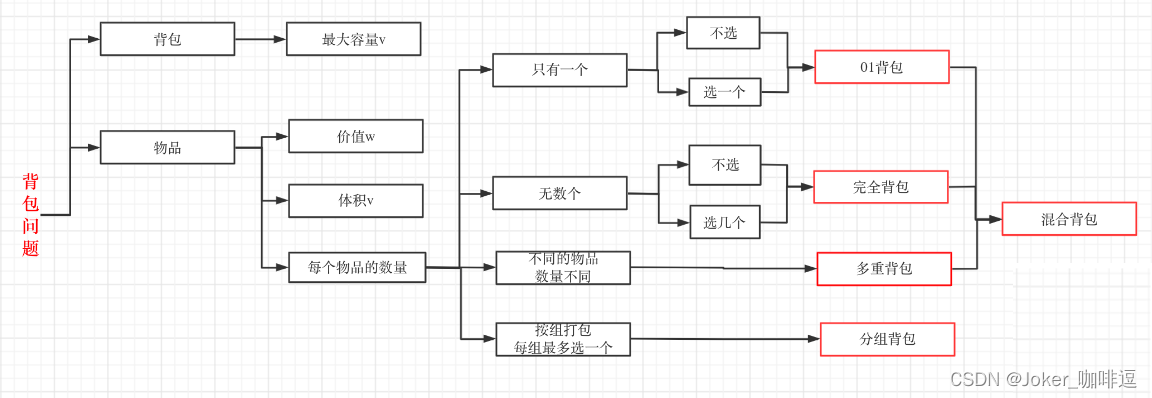
### 1.2 背包问题的分类

背包问题可以分为多个子问题，包括01背包问题、完全背包问题、多重背包问题等。不同类型的背包问题在约束条件和解决方法上有所区别，但核心思想都是通过动态规划等方法来求解最优解。在实际应用中，背包问题被广泛应用于资源分配、物流规划等领域，具有重要的实用价值。

# 2. 01背包问题基础知识

### 2.1 01背包问题的定义
01背包问题是动态规划中经典的问题之一，旨在解决如何在限定重量的情况下，选择物品装入背包以获得最大价值。具体来说，给定n种物品和一个容量为W的背包，每种物品有对应的重量和价值，每种物品仅有一件，求解装入背包的物品组合，使得装入背包的物品总价值最大。

### 2.2 动态规划解决问题的原理
动态规划解决01背包问题的原理在于建立一个二维数组dp，其中dp[i][j]表示在背包容量为j时，在前i件物品中能够获得的最大价值。通过填充这个二维数组，最终找到组合物品的最大总价值。

### 2.3 01背包问题的状态转移方程
01背包问题的状态转移方程可以用数学公式表示为：

dp[i][j] = max(dp[i-1][j], dp[i-1][j-weight[i]] + value[i])

其中，dp[i][j]表示在背包容量为j时，前i件物品能够获得的最大价值；weight[i]表示第i件物品的重量；value[i]表示第i件物品的价值。

接下来，我们将详细探讨01背包问题的状态初始化、状态转移方程的具体推导以及动态规划算法实现步骤。

# 3. 背包问题的动态规划解决

### 3.1 状态初始化
在动态规划解决背包问题时，首先需要对状态进行初始化。具体而言，我们需要创建一个二维数组`dp`，其中`dp[i][j]`表示在前`i`个物品中，背包容量为`j`时能够装下的最大价值。

def knapsack01(weights, values, capacity):
    n = len(weights)
    dp = [[0 for _ in range(capacity + 1)] for _ in range(n + 1)]
    # 初始化第一行和第一列为0
    for i in range(1, n + 1):
        for j in range(1, capacity + 1):
            if weights[i - 1] > j: