案例分析：如何有效处理偏差与方差问题

# 1. 偏差与方差问题的理论基础

在机器学习领域，模型的性能评估不仅仅在于其预测结果的准确性，还涉及到两个重要的概念——偏差和方差。偏差与方差问题是模型泛化能力的核心体现，它们描述了模型对于训练数据的拟合程度以及对新数据的适应能力。

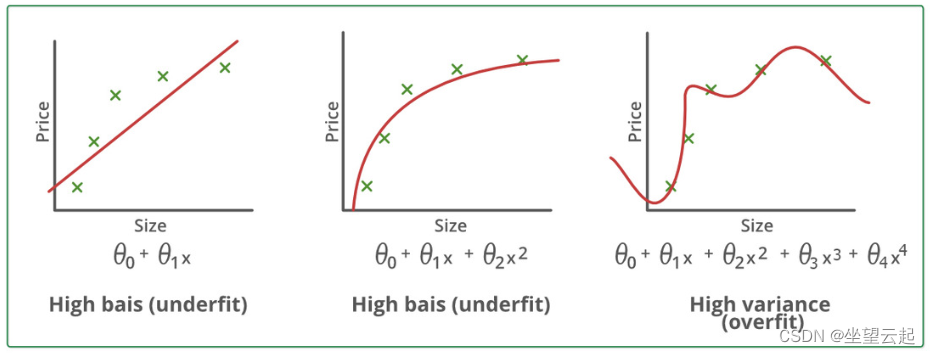
偏差(Bias)衡量的是模型预测的平均结果与真实值之间的差异，它反映了一个模型的预测值偏离真实值的程度。一个具有高偏差的模型倾向于简化假设，从而忽略数据中的复杂性，这往往导致模型对训练集和测试集都拟合得不好，即出现欠拟合现象。

方差(Variance)则描述了模型预测值的波动程度，也就是当训练集变动时，模型预测结果的稳定性。一个模型如果具有高方差，意味着它对于训练数据过分敏感，从而在面对新的数据集时，其表现可能会大相径庭，表现为过拟合。

理解偏差与方差对优化机器学习模型至关重要。偏差与方差之间的权衡，有时被形象地称为偏差-方差权衡（Bias-Variance Tradeoff），是构建和选择机器学习模型时必须考虑的关键因素。在后续章节中，我们将深入探讨偏差与方差的概念，诊断方法以及如何在实际操作中减少偏差和方差，以达到提高模型泛化性能的目的。

# 2. 理解偏差与方差的概念

### 2.1 偏差的概念及其影响

#### 2.1.1 偏差定义及其在模型性能中的角色

偏差（Bias）是机器学习模型在训练数据上表现出来的平均预测误差，是模型的预测值与真实值之间差异的量度。偏差低意味着模型能够准确地捕捉到数据中的真实关系，高偏差则意味着模型与真实情况存在较大偏差，通常导致模型过于简化，无法准确捕捉数据的特征。

在模型性能评估中，偏差与方差共同决定了模型的泛化能力。一个理想的学习算法应当同时拥有低偏差和低方差，即能够准确地在训练数据上学习，并在新的未见过的数据上表现良好。但在实际中，偏差和方差往往存在权衡，即降低一方可能导致另一方增加，这是机器学习领域著名的偏差-方差权衡（Bias-Variance Tradeoff）问题。

#### 2.1.2 高偏差引起的欠拟合问题

高偏差通常与欠拟合（Underfitting）相关联。欠拟合是指模型过于简单，以至于无法捕捉数据中的基本趋势和模式。这样的模型不仅在训练集上表现不佳，而且在新的测试集上的表现也同样差。

解决高偏差问题通常需要增加模型的复杂度，比如提高多项式的阶数、增加决策树的深度等。在深度学习中，可以增加网络的层数或神经元的数量，或者改变网络结构以更好地学习数据的分布。但值得注意的是，增加模型复杂度可能会导致过拟合（Overfitting），这就需要我们进一步考虑如何平衡偏差和方差。

### 2.2 方差的概念及其影响

#### 2.2.1 方差定义及其在模型性能中的角色

方差（Variance）衡量的是模型对于不同数据集的敏感程度，即模型预测值的变动范围。高方差意味着模型对于训练数据中的随机误差非常敏感，从而导致在新数据上的表现不佳。简而言之，高方差的模型可能在训练集上表现很好，但在不同的数据集（尤其是测试集）上表现不佳。

方差的高低直接影响模型的泛化能力。当一个模型对训练数据中的噪声也进行学习，而不是仅仅学习数据的底层规律时，就会出现高方差的情况。这种情况下，模型可能在训练数据上有着很高的准确度，但是在未知数据上的性能可能会大打折扣。

#### 2.2.2 高方差引起的过拟合问题

高方差通常与过拟合（Overfitting）紧密相关。过拟合是指模型在训练数据上表现得非常好，但在新的未见过的数据上表现较差。这通常是由于模型过于复杂，以至于它开始记忆训练数据中的噪声和细节，而不是学习数据的通用规则。

为了降低模型的方差，常用的方法包括简化模型、增加数据量、正则化方法以及应用集成学习等。在简化模型时，需要谨慎地选择模型复杂度以避免陷入欠拟合。增加数据量也是一种有效的方法，因为更多的数据可以帮助模型更好地泛化。正则化技术通过给模型的学习过程添加约束来防止过拟合。集成学习则是通过组合多个模型来减少总体的方差。

在理解了偏差与方差的概念及其对模型性能的影响之后，我们接下来将探讨如何诊断模型中的偏差和方差问题，以及如何通过实际操作对模型进行调整以解决这些问题。

# 3. 偏差与方差的诊断方法

偏差与方差是衡量机器学习模型泛化能力的关键指标。在模型开发的过程中，理解如何诊断偏差和方差，以及如何通过诊断结果来优化模型，是数据科学家必须掌握的技能。本章将深入探讨偏差与方差的诊断方法，并为读者提供实际操作的指导和案例分析。

## 3.1 数据集划分与交叉验证

在机器学习的实践中，数据集通常被划分为训练集、验证集和测试集。这种划分有助于我们从不同的角度评估模型的性能，并诊断偏差与方差。

### 3.1.1 训练集、验证集和测试集的划分方法

为了准确地评估模型的泛化能力，我们通常采用以下步骤来划分数据集：

1. 将原始数据集随机分为K个大小相等的子集。
2. 选择其中的一个子集作为测试集，其余的K-1个子集全部作为训练数据。
3. 将训练数据再次划分为训练集和验证集。这可以通过另一种随机分割完成，或者通过交叉验证的方式来实现。
4.