从理论到实践：如何在算法选择中运用偏差-方差权衡

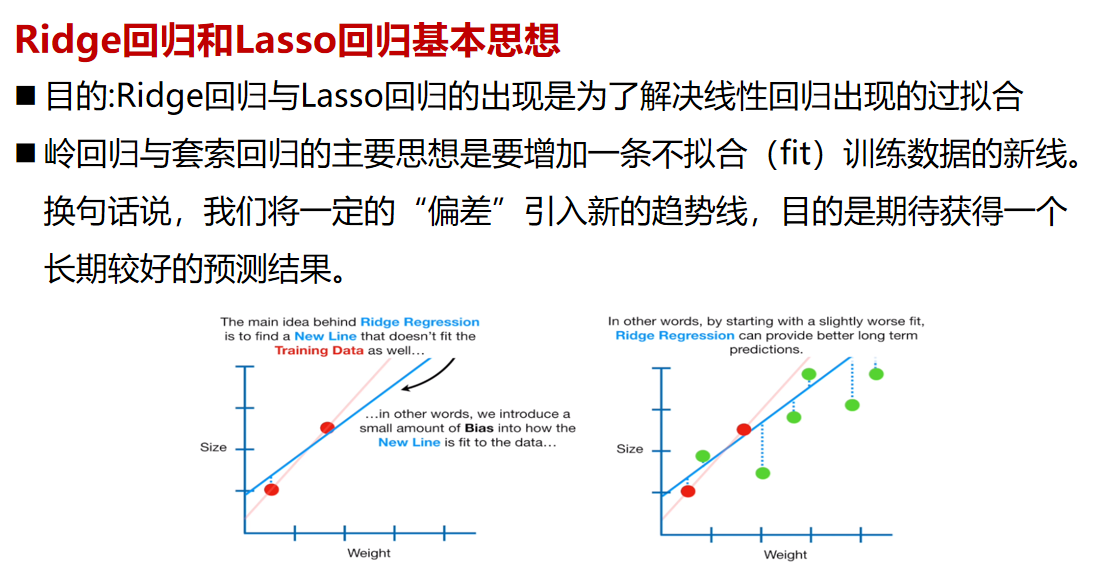
# 1. 偏差-方差权衡理论概述

偏差-方差权衡是机器学习领域中一个核心概念，它描述了模型复杂度与学习算法性能之间的关系。简而言之，模型过度复杂可能导致过拟合，即高方差；而模型过于简单则可能导致欠拟合，即高偏差。本章将为读者介绍这一理论的基础知识，为深入理解和应用偏差-方差权衡奠定基础。

在接下来的章节中，我们将详细探讨偏差和方差的定义，它们各自对模型的影响，以及模型复杂度是如何与两者相互作用的。理解这些概念对于选择合适的机器学习模型、优化算法性能至关重要。同时，我们还将探究如何在实际应用中权衡偏差和方差，以达到最佳的模型性能。这一理论不仅在算法选择和模型调优中起到关键作用，也为机器学习的实践提供了理论支撑和操作指导。

# 2. 偏差和方差的基本概念

### 2.1 统计学中的偏差与方差
#### 2.1.1 偏差的定义及其对模型的影响

偏差（Bias）是统计学和机器学习中的一个重要概念，它衡量的是模型预测值与真实值之间的平均差异。更具体地，偏差反映了模型预测的一致性，即模型对于同一批数据反复做出的预测是否稳定一致。如果一个模型在训练数据上表现很好，但在新的、未见过的数据上表现不佳，那么它可能具有高偏差。

在模型构建过程中，如果一个模型过于简单，如线性模型在面对非线性数据时，它可能无法捕捉到数据中的真实关系，从而导致高偏差。这样的模型可能会在训练集上表现欠佳，因为它无法准确地学习到数据的真实分布。然而，在某些情况下，简单的模型由于其过度的泛化能力，可能会在未见数据上表现得比复杂模型好。这是因为复杂模型可能会过度拟合到训练数据的噪声，导致在新数据上的表现不佳。

#### 2.1.2 方差的定义及其对模型的影响

方差（Variance）在统计学中描述了一个数据集的离散程度，它衡量的是模型预测值的波动性或不稳定性。在机器学习中，方差指的是模型对于不同的训练数据集的表现差异。高方差的模型可能会对训练数据中的噪声过度敏感，从而在训练集上表现出色，但泛化到新数据集时表现差。

例如，当使用决策树进行分类时，如果树模型过于复杂（如深度过大），则可能会学习到训练数据中的随机波动和异常值。这种模型在训练集上的准确率可能会非常高，但在独立的测试集上的准确率却很差。因为这样的模型无法有效推广到未知数据上，它在面对新的数据分布时会表现出高度的不稳定性。

### 2.2 模型复杂度与偏差-方差的关系

#### 2.2.1 模型复杂度对偏差的影响

模型复杂度（Complexity of Model）通常与模型能够拟合数据的程度成正比。在一定程度上，增加模型复杂度可以减少偏差，因为它提供了更强大的表示能力来捕捉数据中的复杂关系。然而，当模型过于复杂时，可能会导致过拟合，此时模型不是在学习数据的真实分布，而是在学习数据中的噪声，这将导致高偏差。

例如，在多项式回归中，通过增加多项式的阶数可以更灵活地拟合数据。然而，过高的阶数可能会使模型在训练集上表现良好，但在新的数据集上却不能很好地泛化。因此，模型复杂度与偏差之间的关系是一个倒U型曲线：随着复杂度的增加，模型的偏差会首先下降，达到一定程度后，再增加复杂度反而会导致偏差的上升。

#### 2.2.2 模型复杂度对方差的影响

同样地，模型复杂度对方差也有类似的影响。较低复杂度的模型通常对数据的噪声不那么敏感，具有较低的方差。但是，当模型复杂度过低时，它可能无法捕捉到数据中的关键特征，导致模型在训练和测试集上的表现都不理想。

以一个简单的线性回归模型为例，它可能无法很好地描述一个明显非线性的关系。此时，增加模型复杂度（例如，使用非线性模型或增加多项式项）可以降低模型的方差，因为它提供了更好的能力来适应数据。然而，如果模型过于复杂，它可能会过度拟合到训练数据，导致泛化能力下降，表现为高方差。

### 实践中的应用

为了更好地理解偏差和方差之间的权衡关系，我们可以考虑在实践中如何调整模型复杂度以优化性能。调整模型复杂度的一种常见方法是通过选择合适的模型参数。在诸如决策树这样的模型中，树的深度是一个关键参数，它直接决定了模型的复杂度。通过交叉验证等技术，我们可以找到最佳的树深度，这样既能保证模型能够学习到数据中的重要结构，又能避免学习到噪声。

为了进一步说明，让我们看一个简单的线性回归模型的代码示例，并观察如何调整多项式度数来平衡偏差和方差。

from sklearn.linear_model import LinearRegression
from sklearn.preprocessing import PolynomialFeatures
from sklearn.pipeline import make_pipeline
import numpy as np
import matplotlib.pyplot as plt

# 生成一些简单的线性数据
np.random.seed(0)
X = 2 * np.random.rand(100, 1)
y = 4 + 3 * X + np.random.randn(100, 1)

# 创建一个多项式回归模型
degree = 1
model = make_pipeline(PolynomialFeatures(degree), LinearRegression())
model.fit(X, y.ravel())

# 生成图表以展示结果
X_test = np.linspace(0, 2, 100).reshape(100, 1)
y_pred = model.predict(X_test)
plt.scatter(X, y, edgecolor='b', s=20, label='data')
plt.plot(X_test, y_pred, color='r', label='degree = %d' % degree)
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.show()

在这个例子中，我们首先生成了一些简单的线性数据，然后使用`PolynomialFeatures`和`LinearRegression`来创建一个简单的多项式回归模型。通过改变`degree`变量，我们可以调整模型复杂度，并观察模型性能的变化。

在实际应用中，我们可能需要通过交叉验证来选择最佳的多项式度数。通过这种方式，我们可以在保证模型不因复杂度过高而学习到噪声（即低方差）和不因复杂度过低而无法捕捉数据的真实关系（即低偏差）之间取得平衡。

下图展示了调整模型复杂度（多项式度数）如何影响模型在数据上的拟合：

graph TD
    A[简单模型] --> B[复杂模型]
    B --> C[过拟合模型]
    C -->|增加复杂度| D[方差增大]
    A -->|减少复杂度| E[偏差增大]

通过上述图表，我们可以看到，随着模型复杂度的增加，模型在训练数据上的表现会越来越拟合（方差降低），但是当复杂度过高时，模型可能会在新数据上表现差，即出现过拟合现象（方差增大）。同理，如果我们降低模型复杂度，可能会导致欠拟合（偏差增大）。因此，我们需要通过不断尝试和验证来找到一个最优的平衡点。

# 3. 在算法选择中应用偏差-方差权衡

在构建预测模型的过程中，算法选择是决定最终模型性能的关键步骤之一。偏差-方差权衡作为机器学习理论中的一个核心概念，为算法选择提供了理论指导。理解并应