量化模型性能：偏差与方差的精确评估与调整方法

# 1. 偏差与方差的基本概念

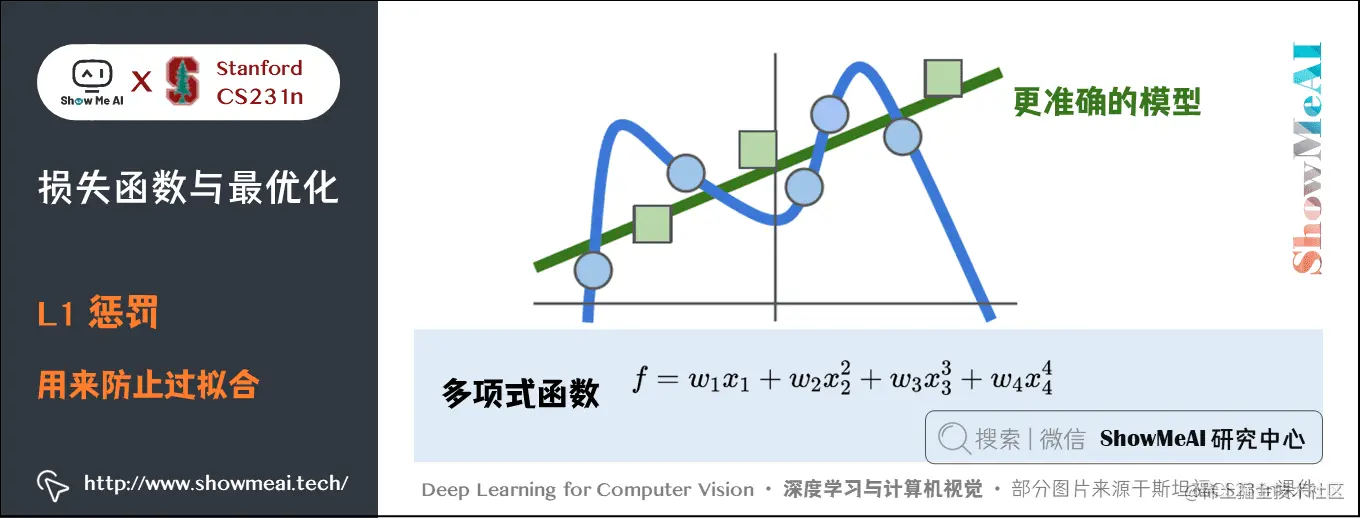
在机器学习领域，偏差与方差是评估模型性能的两个核心概念。偏差反映的是模型的预测值与真实值之间的差距，描述了模型的“泛化误差”，即模型在未见过的数据上的表现。偏差较低的模型通常意味着它能够较好地捕捉到数据中的真实关系。而方差则描述了模型预测值的离散程度，即模型在不同训练集上的表现是否一致。

理解偏差与方差的关键在于认识到它们之间的权衡关系，这一关系在统计学习理论中被称作偏差-方差权衡（Bias-Variance Tradeoff）。模型如果太简单，可能会导致高偏差，即它无法捕捉数据中的所有重要信息；而模型如果太复杂，则可能产生高方差，即它可能会对训练数据的随机噪声过度拟合。

总结来说，偏差与方差的概念为我们提供了理解和衡量模型性能的工具，帮助我们在模型复杂度和泛化能力之间寻找最佳平衡点。接下来的章节将深入探讨如何量化模型性能，并详细说明偏差与方差的理论框架及其计算方法。

# 2. 量化模型性能的理论框架

在探讨模型性能时，我们首先需要一个理论框架来评估和理解模型的表现。在本章中，我们将深入探讨偏差与方差在模型性能评估中的重要角色，并介绍相关的数学基础。此外，我们还将构建理论模型，为后续的实证分析提供坚实的基础。

### 2.1 性能评估的重要性

在机器学习和统计模型中，量化模型性能是一个核心问题。准确的性能评估可以帮助我们了解模型的优缺点，指导我们进行模型选择和调优。

#### 2.1.1 评估指标的选取

模型性能的评估指标必须能够准确反映出模型在预测时可能出现的偏差和方差。常见的一些指标包括均方误差（MSE）、准确率、召回率、F1分数等。根据具体的应用场景和需求，我们可以选择一个或多个指标进行模型的性能评估。

# 示例：计算均方误差
def mean_squared_error(y_true, y_pred):
    return np.mean((y_true - y_pred) ** 2)

上述代码定义了均方误差的计算方法，它是预测值与真实值差的平方的均值。对于回归问题，MSE 是评估模型性能的一个常用指标。

#### 2.1.2 性能评估的实验设计

实验设计在性能评估中同样重要。我们需要确保评估过程公正无偏，以真实反映模型在未知数据上的表现。通常，我们采用的方法是数据分割，包括训练集、验证集和测试集的划分。这有助于我们在训练过程中优化模型参数，并在最终阶段评估模型的泛化能力。

### 2.2 偏差与方差的数学基础

为了更好地理解模型的性能，我们需要了解预测误差的分解，这涉及偏差和方差的概念。

#### 2.2.1 预测误差的分解

在统计学中，预测误差可以分解为偏差、方差和不可约误差。其中，偏差反映了模型预测平均值与真实值之间的差异，方差则反映了模型预测值的波动程度，即模型对样本数据变化的敏感性。

# 示例：计算偏差和方差
def calculate_bias_variance(true_values, predictions):
    mean_predictions = np.mean(predictions, axis=0)
    bias = np.mean((mean_predictions - true_values) ** 2)
    variance = np.mean(np.var(predictions, axis=0))
    return bias, variance

此函数计算了一组预测值的偏差和方差。通过对模型预测进行平均和求方差，我们可以得到偏差和方差的具体数值。

#### 2.2.2 偏差和方差的定义与数学表达

偏差（Bias）是模型预测的系统性误差，而方差（Variance）是模型预测的随机性误差。在数学上，偏差和方差可以表示为：

- 偏差（Bias）：\( Bias = E[\hat{f}(x_0)] - f(x_0) \)
- 方差（Variance）：\( Var(\hat{f}(x_0)) = E[(\hat{f}(x_0) - E[\hat{f}(x_0)])^2] \)

其中，\( \hat{f}(x_0) \) 是模型对输入 \( x_0 \) 的预测，\( f(x_0) \) 是真实的目标函数值，\( E \) 是期望值。

### 2.3 理论模型的构建

构建理论模型是理解偏差与方差关系的基础。

#### 2.3.1 假设空间的概念

假设空间是所有可能的学习模型的集合。在机器学习中，我们通过在假设空间中选择最合适的模型来进行学习。偏差和方差会随着假设空间的复杂度而变化，复杂模型容易过度拟合而产生高方差，而简单模型可能会导致高偏差。

#### 2.3.2 模型复杂度的度量

模型复杂度可以通过多种方式度量，例如模型参数的数量、模型的决策边界复杂性等。理解模型复杂度有助于我们平衡偏差和方差，找到最佳的模型性能。

# 示例：模型复杂度度量 - 参数数量
def model_complexity(model):
    return len(model.get_params())

在此代码中，我们定义了一个简单的函数来度量模型复杂度，通过计算模型参数的数量。这只是复杂度度量的一种方式，实际应用中可能需要更复杂的方法来准确评估模型复杂度。

接下来，我们将深入第三章，探讨偏差与方差的计算方法，以及在实证分析中如何应用这些理论知识。

# 3. 偏差与方差的计算方法

## 实证分析中的偏差评估

偏差（Bias）衡量的是模型预测值的平均数与真实值之间的差异。在统计和机器学习模型的评估中，偏差往往与过拟合现象相关联。偏差过高通常意味着模型对于训练数据的拟合不够，模型无法捕捉到数据中的规律，导致预测结果系统性地偏离真实值。

### 交叉验证技术

交叉验证是统计学中一种常用的评估模型性能的方法，它通过将原始数据分成K个子集，然后进行K次模型训练和验证，每次使用不同的子集作为验证集，而剩下的子集作为训练集，最后取所有验证集上模型性能的平均值作为最终的性能评估指标。

为了计算偏差，我们可以使用如下的步骤：

1. 将数据集随机划分成K个大小相同的子集。
2. 依次选取其中的一个子集作为验证集，其余的K-1个子集用于训练模型。
3. 记录下每次训练模型在验证集上的性能评估指标。
4. 最后，计算所有K次评估指标的平均值。

通过交叉验证，我们能够更好地了解模型在不同数据子集上的表现，并减少因数据划分不同而带来的评估波动。

### 偏差评估的实例分析

假设我们有一个回归问题，目标是预测房价。我们可以选择均方误差（Mean Squared Error, MSE）作为性能评估指标。使用5折交叉验证，我们得到以下5次实验的MSE值：

MSE1 = 1.2, MSE2 = 1.4, MSE3 = 1.3, MSE4 = 1.1, MSE5 = 1.5

计算平均值，我们得到：

Average MSE = (1.2 + 1.4 + 1.3 + 1.1 + 1.5) / 5 = 1.3

这个平均MSE值即为模型在偏差上的评估结果。如果这个值相对较高，这可能意味着我们的模型在训练过程中不能很好地捕捉数据中的关系，存在系统性的误差。

## 实证分析中的方差评估

与偏差不同的是，方差衡量的是模型预测值的一致性。方差越大，意味着模型在不同训练集上得到的模型差异越大，表现为模型不够稳定，容易受到训练数据的波动影响，即高方差与模型欠拟合相关。

### 方差分析方法

为了计算模型的方差，可以按照以下步骤进行：

1. 重复上述交叉验证的过程