如何评估卡尔曼滤波算法在实际项目中的性能表现？

# 1. 理解卡尔曼滤波算法

在现代技术应用中，卡尔曼滤波算法扮演着重要角色。该算法是一种递归数据处理技术，结合系统动态模型和测量数据，通过状态估计来减小噪声干扰，提高系统稳定性和精度。其核心概念包括状态空间模型、测量更新和预测更新。通过状态估计的迭代过程，卡尔曼滤波能够有效处理复杂系统的动态变化，适用于多种场景，如目标跟踪、导航系统等。卡尔曼滤波算法的优势在于能够在噪声环境下快速准确地估计系统状态，具有较高的计算效率和稳定性。深入理解和应用卡尔曼滤波算法对于提高数据处理和系统控制的准确性至关重要。

# 2. 选择合适的模型

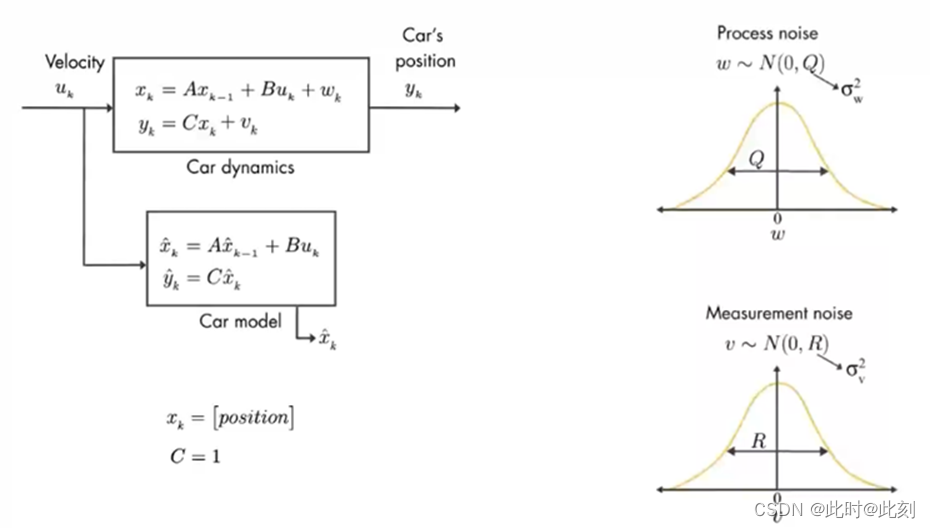
在实际项目中应用卡尔曼滤波算法时，首先需要选择合适的模型来描述系统的动态特性。这个过程包括确定系统的动态模型、噪声协方差以及观测模型。只有通过准确地建立模型，卡尔曼滤波算法才能发挥最佳的性能，从而实现对系统状态的高效估计和跟踪。

### 确定系统动态模型

确定系统的动态模型是卡尔曼滤波算法设计的关键一步。动态模型描述了系统状态如何随时间演变，即系统的状态转移方程。在确定动态模型时，需要考虑系统的运动学特性和外部干扰因素，以确保模型能够准确地反映系统的运动规律。

### 确定噪声协方差

在实际系统中，往往存在来自外部环境和传感器测量的噪声。噪声协方差矩阵 Q 和 R 是卡尔曼滤波算法中用来描述过程噪声和测量噪声的重要参数。通过准确估计噪声的协方差，可以更好地优化卡尔曼滤波算法的性能，提高对系统状态的估计精度。

### 确定观测模型

观测模型定义了系统状态与观测之间的关系，即如何将系统状态映射到观测空间。观测模型通常由观测矩阵 H 表示，它描述了系统状态和观测之间的线性关系。在确定观测模型时，需要充分考虑系统的传感器类型和观测数据的特点，以确保准确地获取观测信息并进行有效的状态更新。

## 卡尔曼滤波在轨迹跟踪中的应用

卡尔曼滤波算法在轨迹跟踪领域有着广泛的应用，其中包括目标跟踪和自主车辆导航。通过有效地建模系统动态特性和优化观测更新过程，卡尔曼滤波能够实现对目标运动状态和车辆位置的精确跟踪，为实时导航和路径规划提供可靠的支持。

### 目标跟踪

在目标跟踪中，首先需要对目标的运动行为进行建模，包括速度、加速度等动态特性。通过状态空间模型和观测信息更新，可以实现对目标位置的准确推测和轨迹预测，从而实现目标的持续跟踪和动态定位。

#### 目标运动建模

通过建立目标的动态状态方程，可以描述目标的运动轨迹和速度变化规律。根据目标的实际运动情况，可以选择合适的运动模型，如常速度模型、匀加速度模型等，以实现对目标运动状态的有效估计。

#### 观测更新

观测更新过程通过将实际观测值与预测状态进行比较，校正状态估计并更新滤波器的内部状态。在目标跟踪中，观测更新过程能够帮助准确地获得目标位置信息，并调整状态估计值，从而实现对目标轨迹的实时跟踪和更新。

#### 轨迹预测

通过状态空间模型和卡尔曼滤波算法，可以进行轨迹的预测和目标位置的估计。轨迹预测使系统能够提前预测目标的运动轨迹，为后续动作做出合理规划和调整，从而实现对目标的精确跟踪和预测。

### 自主车辆导航

在自主车辆导航中，卡尔曼滤波算法可用于整合多传感器数据、规划车辆路径以及实时调整导航方案，从而实现自主车辆沿着设定路径安全导航和避障。

#### 传感器数据整合

自主车辆通常装备有多种传感器，如惯性测量单元（IMU）、全球定位系统（GPS）、激光雷达等，用于感知车辆周围环境和定位车辆位置。通过卡尔曼滤波算法可以有效整合多传感器数据，提高车辆位置估计的准确性。

#### 路径规划

基于车辆当前位置和目标位置