什么是卡尔曼滤波算法？初探其基本原理和应用

# 1.1 什么是滤波算法

滤波算法是一种用于处理数据的技术，通过消除信号中的噪声和干扰，提取出有用信息。滤波算法在传感器数据处理、信号处理、图像处理等领域广泛应用。其中，卡尔曼滤波算法是一种最为经典和有效的滤波方法之一，通过对系统状态进行估计和预测，实现对变量的精准跟踪和预测。在实际应用中，卡尔曼滤波算法能够有效地处理动态系统中存在的不确定性，并具有良好的收敛性和稳定性。因此，了解和掌握滤波算法，特别是卡尔曼滤波算法，对于数据处理和系统建模具有重要意义。

# 2.1 线性系统和状态空间模型

在卡尔曼滤波算法中，我们首先需要了解线性系统和状态空间模型的概念以及它们在算法中的作用。

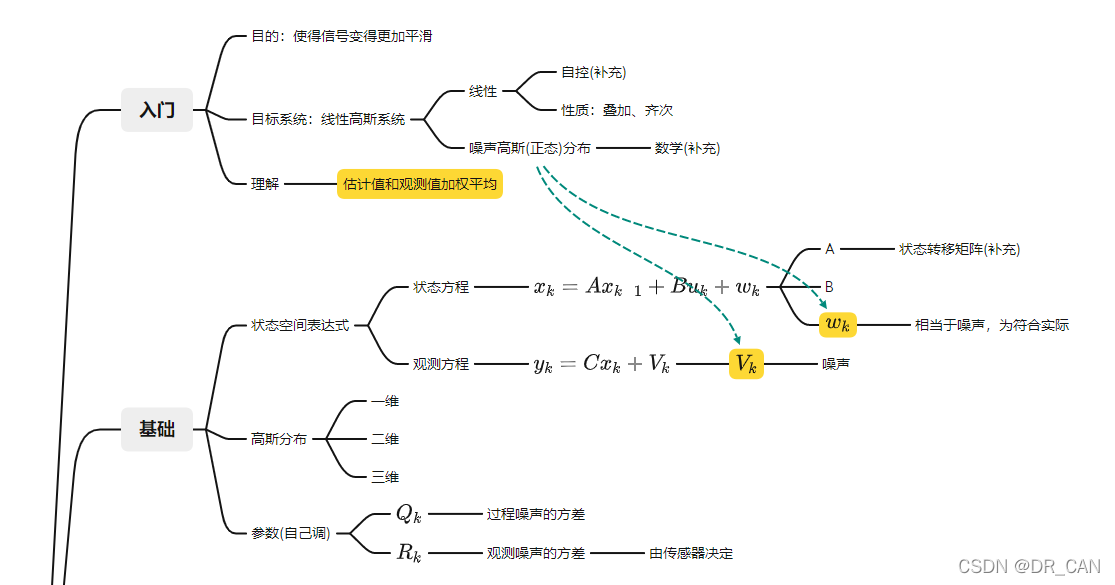
### 2.1.1 状态方程和观测方程

线性系统可以用状态方程和观测方程来描述。状态方程描述系统的状态随时间如何变化，而观测方程则描述系统的状态如何通过观测值映射到观测空间。

状态方程可以表示为：

x_k = A * x_{k-1} + B * u_k + w_k

其中，x_k 是当前时刻的状态，A 是状态转移矩阵，B 是控制输入矩阵，u_k 是控制输入，w_k 是状态转移过程中的噪声。

观测方程可以表示为：

z_k = H * x_k + v_k

其中，z_k 是当前时刻的观测值，H 是观测矩阵，v_k 是观测过程中的噪声。

### 2.1.2 预测和更新步骤

卡尔曼滤波算法主要分为预测和更新两个步骤。在预测步骤中，根据状态方程预测下一时刻的状态；在更新步骤中，根据观测值对预测的状态进行校正，得到最优估计值。

### 2.1.3 协方差矩阵和状态估计

卡尔曼滤波算法通过协方差矩阵来估计状态的不确定性，其中状态的协方差矩阵描述状态估计值与真实状态之间的差异。

状态估计是通过融合预测的状态和观测值来优化估计值，从而减小估计值的误差，提高系统的精确度和鲁棒性。

## 2.2 卡尔曼滤波算法的递归实现

卡尔曼滤波算法的递归实现是指通过逐步迭代的方式，根据当前时刻的状态估计值和协方差矩阵，计算下一时刻的最优估计值和协方差矩阵。

### 2.2.1 预测阶段

在预测阶段，根据状态方程和控制输入，可以通过预测下一时刻的状态和协方差矩阵，同时考虑过程噪声的影响。

预测的状态值和协方差矩阵可以通过以下公式计算：

x_hat_k = A * x_{k-1} + B * u_k
P_k = A * P_{k-1} * A^T + Q

其中，x_hat_k 是预测的状态值，P_k 是预测的协方差矩阵，Q 是过程噪声的协方差矩阵。

### 2.2.2 更新阶段

在更新阶段，根据观测值和预测的状态值，可以通过卡尔曼增益来计算更新后的最优估计值和协方差矩阵，同时考虑观测噪声的影响。

更新后的状态值和协方差矩阵可以通过以下公式计算：

K_k = P_k * H^T * (H * P_k * H^T + R)^(-1)
x_k = x_hat_k + K_k * (z_k - H * x_hat_k)
P_k = (I - K_k * H) * P_k

其中，K_k 是卡尔曼增益，R 是观测噪声的协方差矩阵，I 是单位矩阵。

### 2.2.3 状态更新和误差校正

通过预测和更新步骤的迭代，可以不断更新状态估计值和协方差矩阵，减小状态估计的误差，使系统能够更准确地跟踪状态变化，并提高数据融合的效果。

# 3.1 惯性导航系统中的应用

### 3.1.1 加速计、陀螺仪和磁力计的数据融合

在惯性导航系统中，加速计、陀螺仪和磁力计是常用的传感器，它们分别提供了关于加速度、角速度和方向的信息。通过卡尔曼滤波算法可以将这些传感器提供的数据进行融合，从而得到更加准确和稳定的状态估计。加速计主要用于测量物体的加速度，陀螺仪用于测量物体的角速度，而磁力计则用于确定物体在空间中的方向。通过将这三种传感器的数据进行融合，可以得到更加全面和准确的姿态信息，应用在航位推算和运动跟踪等领域。

### 3.1.2 实时姿态估计

利用卡尔曼滤波算法进行加速计和陀螺仪数据的融合，实现实时姿态估计。通过融合加速计和陀螺仪数据，可以消除各自数据的误差累积问题，得到更加稳定和准确的姿态估计结果。在无人机、航空器等领域，实时姿态估计是非常重要的，可以帮助设备维持正确的方向和姿态，保证其正常运行和控制。

### 3.1.3 航位推算和漂移校正

结合加速计、陀螺仪和磁力计的数据融合，可以实现航位推算和漂移校正。航位推算是指根据已知的起始位置和姿态，结合传感器数据推算物体的当前位置和姿态；而漂移校正则是指通过卡尔曼滤波算法对位置和姿态的估计值进行修正，消除由于传感器误差和累积导致的漂移现象。通过航位推算和漂移校正，可以提高导航系统的准确性和稳定性，应用在需要精确定位和导航的领域。

# 4.1 扩展卡尔曼滤波（EKF）

在实际应用中，很多系统并不是线性的，而是包含非线性因素的。在这种情况下，传统的卡尔曼滤波算法就显得力不从心了。为了解决这个问题，扩展卡尔曼滤波（EKF）应运而生。EKF 是一种基于泰勒级数线性化的滤波算法，通过对非线性函数进行一阶泰勒展开来近似处理非线性系统。

#### 4.1.1 非线性系统的状态空间表达

对于非线性系统，状态方程和观测方程可能并不遵循线性的模型。这就要求我们对系统进行线性近似，以便使用卡尔曼滤波算法。EKF 的核心思想在于使用泰勒级数对非线性函数进行线性化处理，从而得到近似的线性系统模型。

#### 4.1.2 Jacobian 矩阵的计算与更新

在 EKF 中，需要对非线性函数进行泰勒级数展开，然后计算 Jacobi 矩阵。Jacobian 矩阵是系统状态方程和观测方程的偏导数矩阵，用于线性化非线性系统。在实际应用中，需要根据系统具体情况计算和更新 Jacobian 矩阵。

#### 4.1.3 EKF 中的参数调优

在实际应用中，EKF 的性能往往受到许多参数的影响，如过程噪声、观测噪声的协方差矩阵以及状态转移矩阵等。因此，参数的选择对滤波效果至关重要。通常需要通过实际测试和调优来确定最佳的参数配置，以获得最优的滤波效果。

### 4.2 粒子滤波

除了 EKF 外，粒子滤波是另一种用于非线性系统的滤波算法。与传统的卡尔曼滤波算法不同，粒子滤波是一种基于蒙特卡洛采样的滤波方法，它能够更好地处理非线性系统和非高斯噪声情况。

#### 4.2.1 随机采样和重采样

粒子滤波通过随机采样一组粒子来表示系统的状态空间，然后根据观测数据对这些粒子进行加权更新。在不断的迭代中，一些粒子的权重会逐渐变大，而一些粒子的权重会变小甚至消失。为了防止粒子退化，通常会进行重采样来保留具有更高权重的粒子。

#### 4.2.2 粒子权重更新

在粒子滤波中，每个粒子都会根据观测数据和系统模型进行权重更新。通常使用重要性权重来表示每个粒子的重要程度，权重的计算基于观测数据和系统模型的匹配程度。通过有效的权重更新，可以更好地估计系统的状态。

#### 4.2.3 优化粒子滤波算法的效率

尽管粒子滤波在处理非线性系统方面具有优势，但由于其计算复杂度较高，通常需要对算法进行一些优化，以提高运行效率。针对粒子采样和重采样的方法、权重更新的策略以及粒子数目的选择等方面可以进行一些改进，以优化粒子滤波算法的性能。

# 5. 卡尔曼滤波算法的代码实现与案例分析

在本章中，我们将深入探讨卡尔曼滤波算法的具体代码实现，并结合一个简单的案例分析来展示该算法在实际应用中的效果。首先，我们将介绍卡尔曼滤波算法的 Python 实现代码，然后通过一个模拟的二维运动跟踪案例来演示算法的运行过程和结果输出。

### 5.1 Python 实现卡尔曼滤波算法

下面是一个简单的 Python 代码示例，演示了如何使用卡尔曼滤波算法对一维数据进行滤波处理：

import numpy as np

# 初始化卡尔曼滤波器参数
initial_state = 0
initial_guess = 0
initial_guess_variance = 1
process_variance = 0.2
sensor_variance = 0.2

# 初始化状态估计和方差
state_estimate = initial_guess
state_estimate_variance = initial_guess_variance

# 定义卡尔曼滤波函数
def kalman_filter(sensor_measurement):
    global state_estimate, state_estimate_variance
    # 预测阶段
    predicted_estimate = state_estimate
    predicted_estimate_variance = state_estimate_variance + process_variance

    # 更新阶段
    innovation = sensor_measurement - predicted_estimate
    innovation_variance = predicted_estimate_variance + sensor_variance
    kalman_gain = predicted_estimate_variance / innovation_variance
    state_estimate = predicted_estimate + kalman_gain * innovation
    state_estimate_variance = (1 - kalman_gain) * predicted_estimate_variance

    return state_estimate

# 模拟传感器测量数据
measurements = [1, 2, 3, 4, 5]

# 使用卡尔曼滤波器处理数据
filtered_data = []
for measurement in measurements:
    filtered_data.append(kalman_filter(measurement))

print("原始数据：", measurements)
print("滤波后数据：", filtered_data)

在上面的代码中，我们定义了一个简单的一维卡尔曼滤波器，并模拟了一系列传感器测量数据，然后使用卡尔曼滤波算法对这些数据进行滤波处理，最终输出滤波后的结果。

### 5.2 二维运动跟踪案例分析

为了更直观地展示卡尔曼滤波算法的应用效果，我们将以一个简单的二维运动跟踪案例为例进行分析。假设有一个物体沿着直线运动，我们通过一组传感器获取其位置数据，并利用卡尔曼滤波算法对其轨迹进行跟踪。

graph LR
    A[开始] --> B[获取传感器数据]
    B --> C[预测下一时刻状态]
    C --> D[获取测量值]
    D --> E[更新状态估计]
    E --> F{是否结束}
    F -- 是 --> G[输出最终估计值]
    F -- 否 --> C

在上述流程图中，我们首先获取传感器数据，然后通过卡尔曼滤波算法预测下一个时刻的状态，获取测量值后更新状态估计，不断循环直至结束，最终输出最终的估计值。

通过以上代码实现和案例分析，我们可以清晰地了解卡尔曼滤波算法在实际场景中的应用与效果，以及如何通过代码实现来实现算法的功能。在实际项目中，可以根据具体需求对算法进行进一步优化和调整，以满足不同场景下的数据处理需求。

这里只涉及了简单的一维数据处理和二维运动跟踪案例，实际应用中，卡尔曼滤波算法还可以应用于更复杂的多维数据处理和动态系统建模中，具有广泛的应用前景和潜力。