如何选择卡尔曼滤波算法的系统噪声和观测噪声参数？

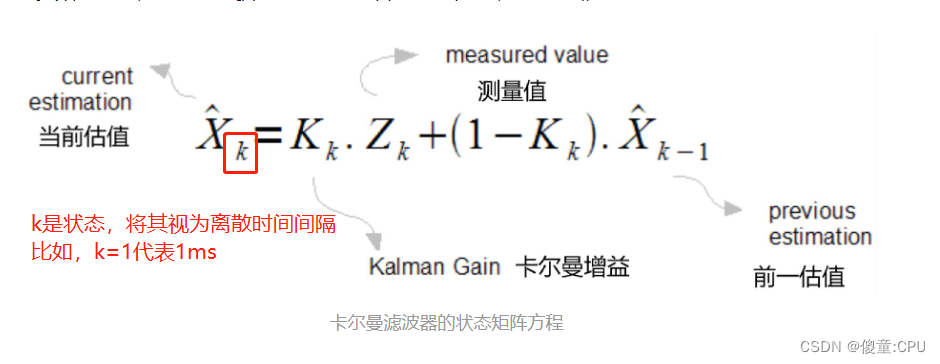
# 1. 卡尔曼滤波算法简介

卡尔曼滤波算法是一种用于估计系统状态的数学方法，通过融合系统模型和实际测量数据，可在噪声干扰下对系统状态进行准确的估计。该算法旨在处理动态系统中存在的不确定性和噪声，广泛应用于导航、控制、信号处理等领域。基本思想是通过状态方程和观测方程对系统状态进行动态估计和更新，以实现对系统状态的精准预测。卡尔曼滤波算法的优势在于能够有效处理非线性系统，并且在数据稀疏或有限的情况下表现出色。因其出色的性能和广泛的应用领域，卡尔曼滤波算法备受工程领域的推崇和应用。

# 2. 卡尔曼滤波算法的核心原理

## 2.1 状态方程和观测方程
卡尔曼滤波算法的核心在于状态方程和观测方程的建模。状态方程描述系统状态如何随时间推移而演化，而观测方程定义了系统状态和观测之间的关系。

### 2.1.1 状态方程的含义和作用
状态方程通常表示为线性动态系统的演化规律，可用数学形式表示为：$x_k = A \cdot x_{k-1} + B \cdot u_k + w_k$，其中 $x_k$ 是系统在时刻 $k$ 的状态向量，$A$ 是状态转移矩阵，$B$ 是控制输入矩阵，$u_k$ 是控制输入，$w_k$ 是系统过程噪声。

### 2.1.2 观测方程的作用及其在算法中的重要性
观测方程定义了系统状态和观测值之间的关系，通常表示为：$z_k = H \cdot x_k + v_k$，其中 $z_k$ 是时刻 $k$ 的观测值，$H$ 是观测矩阵，$v_k$ 是观测噪声。

## 2.2 状态估计和更新过程
在卡尔曼滤波算法中，状态估计和更新是关键步骤，通过预测和更新不断优化系统状态的估计值。

### 2.2.1 预测步骤中的状态估计
预测步骤通过状态方程和控制输入对系统状态进行预测：$\hat{x}_k^- = A \cdot \hat{x}_{k-1} + B \cdot u_k$，其中 $\hat{x}_k^-$ 是时刻 $k$ 的先验状态估计，$\hat{x}_{k-1}$ 是时刻 $k-1$ 的后验状态估计。

### 2.2.2 更新步骤中的状态更新
更新步骤利用观测值来校正状态估计：$K_k = P_k^- \cdot H^T \cdot (H \cdot P_k^- \cdot H^T + R)^{-1}$，$\hat{x}_k = \hat{x}_k^- + K_k \cdot (z_k - H \cdot \hat{x}_k^-)$，$P_k = (I - K_k \cdot H) \cdot P_k^-$，其中 $K_k$ 是卡尔曼增益，$R$ 是观测噪声协方差矩阵，$P_k$ 是状态协方差矩阵。

graph TD;
    A(预测步骤) --> B(计算卡尔曼增益K);
    B --> C(更新状态估计值);
    C --> D(更新状态协方差矩阵P);

通过建立状态方程和观测方程，卡尔曼滤波算法能够在系统动态变化和观测误差的情况下，准确估计系统状态并进行优化。

# 3. 确定系统噪声参数

### 3.1 什么是系统噪声

#### 3.1.1 系统噪声的定义和影响

在卡尔曼滤波算法中，系统噪声指的是系统在状态转移时的不确定性。它