MATLAB控制系统动态性能评估：超调与调节时间分析的高级教程

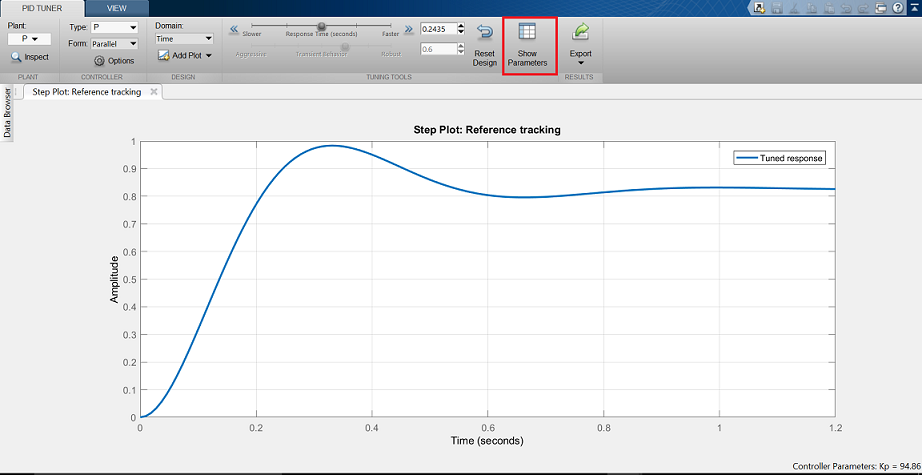
# 1. MATLAB控制系统简介

MATLAB（Matrix Laboratory的缩写）是MathWorks公司推出的一款高性能数值计算和可视化软件。它广泛应用于工程计算、控制系统、信号处理、图像处理和数据可视化等领域。MATLAB的核心是一个高级语言和一个交互式环境，使得用户可以轻松地进行矩阵计算、函数绘图和数据分析。在控制系统领域，MATLAB提供了强大的工具箱，如控制系统工具箱（Control System Toolbox），它包含了一套完整的函数和应用程序，用于分析、设计和模拟控制系统。

控制系统设计师和工程师可以使用MATLAB进行系统的建模、分析和仿真。例如，他们可以模拟系统在特定输入下的响应，评估系统的稳定性和性能指标，设计反馈控制器，以及优化控制系统的参数等。MATLAB不仅提供了方便的数学计算和可视化功能，还能够与Simulink等其他工具协同工作，从而实现更复杂控制系统的建模和实时仿真。

本章将会对MATLAB在控制系统领域的应用做一个基本的介绍，并为接下来章节中更深入的控制系统动态性能分析和MATLAB工具箱的使用奠定基础。

# 2. 控制系统动态性能基础

控制系统动态性能是评估一个系统对输入信号反应能力的重要指标。它不仅决定了系统的响应速度，还关系到系统的稳定性和超调量，是控制工程设计中的核心考量点。

### 2.1 动态性能的核心概念

在深入探讨控制系统动态性能之前，必须先了解两个核心概念：系统响应与超调定义以及调节时间的概念和重要性。

#### 2.1.1 系统响应与超调定义

系统响应是指当输入信号发生突变时，系统的输出随时间变化的行为。一个理想的系统响应应当是快速且准确的。超调量是衡量系统响应质量的一个重要指标，它指的是系统输出超过设定值的最大幅度，通常用百分比表示。例如，在一个比例-积分-微分（PID）控制系统中，超调量过大可能会导致系统的不稳定甚至损坏设备。因此，超调量的控制是动态性能分析的一个关键点。

% MATLAB示例代码：定义并绘制一个简单系统的时间响应
% 创建一个传递函数模型
sys = tf(1, [1, 10, 20]);

% 步跃响应分析
figure;
step(sys);
title('Step Response of a System');
xlabel('Time (seconds)');
ylabel('Amplitude');

% 计算超调量
[~, ~, ~, overshoot] = stepinfo(sys);
disp(['Overshoot percentage: ', num2str(overshoot), '%']);

在MATLAB中，`step`函数可以用来绘制系统的步跃响应，而`stepinfo`函数则用于获取响应特性参数，例如超调量。这为我们提供了分析系统动态性能的初步工具。

#### 2.1.2 调节时间的概念和重要性

调节时间是指系统输出从开始响应到最终稳定在设定值附近的时间。对于控制系统来说，一个短的调节时间意味着系统能够快速达到稳定状态，这对于工业控制来说是至关重要的。例如，在一个温度控制系统中，快速稳定温度可以减少能源浪费并提高生产效率。

% MATLAB示例代码：计算并显示系统的调节时间
% 设置系统模型的参数
sys = tf(1, [1, 10, 20]);

% 调节时间分析
[~, ~, ~, settleTime] = stepinfo(sys);
disp(['Settling Time: ', num2str(settleTime), ' seconds']);

这段代码使用`stepinfo`函数计算调节时间，并展示其在控制系统的应用场景。调节时间是一个重要的性能指标，它直接关联到系统效率和可靠性。

### 2.2 控制系统的基本性能指标

控制系统的设计和评估需要依据一系列的基本性能指标，包括稳定性、稳态误差、上升时间和峰值时间。

#### 2.2.1 稳定性与稳态误差

稳定性是控制系统设计的首要目标。系统在受到干扰或变化的输入信号后，应能保持输出在一个可接受的范围内。稳定性可以通过系统的极点位置或Routh-Hurwitz判据来判断。稳态误差是系统在稳态时的误差，通常我们希望这个值尽可能小。

% MATLAB示例代码：分析系统的稳定性并计算稳态误差
% 创建一个传递函数模型
sys = tf(1, [1, 10, 20]);

% 判断系统的稳定性
poleLocations = pole(sys);
disp('Pole Locations:');
disp(poleLocations);

% 计算稳态误差
ssError = 1 / (1 + feedback(sys, 1));
disp(['Steady-state error: ', num2str(ssError)]);

通过计算系统的极点位置和使用反馈结构，我们可以评估系统的稳定性和计算稳态误差。这有助于我们了解系统在长期运行中的性能表现。

#### 2.2.2 上升时间与峰值时间

上升时间是指系统输出从其最终稳态值的10%上升至90%所需的时间。它直接关联到系统的响应速度，对于要求快速响应的系统来说尤为重要。峰值时间则是输出达到第一个峰值所需的时间，它也是系统性能的一个关键指标。

% MATLAB示例代码：计算上升时间和峰值时间
% 创建一个传递函数模型
sys = tf(1, [1, 10, 20]);

% 计算上升时间和峰值时间
上升时间 = riseTime(sys);
峰值时间 = peakTime(sys);
disp(['Rise Time: ', num2str(上升时间), ' seconds']);
disp(['Peak Time: ', num2str(峰值时间), ' seconds']);

以上MATLAB代码展示了如何利用控制系统工具箱中的函数计算上升时间和峰值时间。这两个参数对于理解系统在短时间内动态响应特性具有重要意义。

控制系统动态性能的探讨是一个深入而广泛的话题，从基础概念到具体的应用和分析，都有大量的理论与实践相结合的知识点。在后续章节中，我们将更深入地探讨如何利用MATLAB这一强大的工具，对控制系统进行更详尽的分析和优化。

# 3. MAT