MATLAB控制系统PID控制器设计：理论与实践的完美结合

# 1. PID控制器的基础理论

## 1.1 PID控制器的简介
PID控制器（比例-积分-微分控制器）是工业控制领域应用最为广泛的反馈控制器。它通过计算偏差或其积分（累积误差）和微分（误差变化率）来实现对系统的控制。PID控制器主要由比例（P）、积分（I）、微分（D）三个基本参数构成，通过它们的线性组合来形成控制量，以达到对系统的快速、准确控制。

## 1.2 PID控制的作用原理
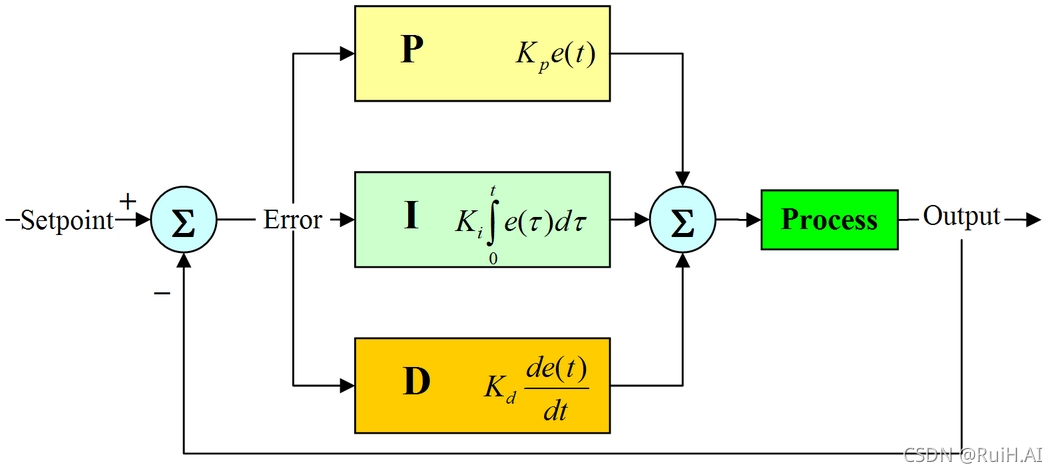
在系统中，当存在一个期望设定值（Set Point, SP）和一个实际输出值（Process Variable, PV）时，二者的差值即为偏差（Error, e），PID控制器的作用就是计算这个偏差并根据P、I、D三个参数的权重，输出一个控制量（Controller Output, CO），以此来调整系统以消除偏差。

比例部分（P）对当前误差进行响应，积分部分（I）是误差的累计，用于消除稳态误差，而微分部分（D）则响应误差的变化率，预测未来的误差变化趋势，对系统的动态特性进行优化。

## 1.3 PID控制器的应用场景
PID控制器广泛应用于各种控制系统中，比如温度控制、速度控制、压力控制等。因其结构简单，易于实现和调整，所以它尤其适用于对动态特性要求不是特别高的场合。同时，通过合适参数的调整，PID控制器也可以在一些更为复杂的系统中发挥作用。随着工业自动化和智能化的发展，PID控制器通常与其他控制策略结合，形成更加复杂和高效的控制系统。

# 2. MATLAB环境下PID控制器的设计

## 2.1 MATLAB工具箱与控制系统设计基础

### 2.1.1 MATLAB控制系统工具箱概述

MATLAB提供了专门的工具箱用于控制系统的设计与分析，其中控制系统工具箱（Control System Toolbox）是最为重要的一个，它包含了丰富的方法和函数来帮助工程师进行控制器设计、系统分析以及创建和操作控制模型。

控制系统工具箱中包括了各类函数，能够执行线性系统分析（比如传递函数和状态空间模型）、设计控制器（如PID控制器）以及对系统进行模拟仿真等。在设计PID控制器时，MATLAB能够帮助工程师计算参数、模拟系统响应，还能进行参数的自动调节（如利用PID Tuner工具）。

在MATLAB的控制系统工具箱中，工程师可以利用`tf`、`ss`、`zpk`等函数进行系统模型的创建。模型建立之后，可以利用`step`、`bode`、`nyquist`等函数来进行系统的稳定性分析和频率响应分析。除了手动计算和分析，工具箱内还提供了交互式设计工具如PID Tuner，它可以帮助工程师快速地获得满足性能要求的PID控制器参数。

### 2.1.2 控制系统建模的基本方法

控制系统建模是设计控制器前的一个重要步骤。在MATLAB环境下，建模可以通过多种方式实现，包括：

- 利用微分方程直接定义系统的动态特性。
- 通过传递函数（Transfer Function）表示系统的输入输出关系。
- 使用状态空间（State-Space）模型来描述系统的内部状态变量。

例如，通过传递函数定义一个简单的一阶系统：

num = 1; % 分子
den = [1, 3, 2]; % 分母
sys = tf(num, den);

这段代码创建了一个传递函数模型`sys`。状态空间模型则可以通过`ss`函数创建，例如：

A = [-1, -2; 1, 0];
B = [1; 0];
C = [0, 1];
D = 0;
sys_ss = ss(A, B, C, D);

这里创建了一个状态空间模型`sys_ss`。无论是哪种建模方式，MATLAB都提供了相应的分析和设计工具，以便工程师可以轻松地进行控制系统的设计和仿真。

## 2.2 PID控制器参数的理论计算

### 2.2.1 比例（P）、积分（I）、微分（D）的作用与关系

PID控制器是一种常见的反馈控制器，其核心由比例（P）、积分（I）和微分（D）三个环节组成。理解每个环节的作用及其在系统中的相互关系，是进行PID参数计算的基础：

- **比例（Proportional, P）**：比例环节反映了控制器输出与偏差信号的大小关系。比例系数（Kp）越大，对偏差的反应就越敏感，但也可能引起系统振荡。
- **积分（Integral, I）**：积分环节基于偏差信号的累积值来计算。积分系数（Ki）决定了对长期累积偏差的补偿力度，有助于消除稳态误差，但过大可能会导致系统响应速度变慢。
- **微分（Derivative, D）**：微分环节对偏差的变化率进行反应。微分系数（Kd）决定了对快速变化的响应程度，有助于改善系统的动态响应，减少超调，但对噪声较为敏感。

理想情况下，比例环节能够提供快速的响应，积分环节可以消除稳态误差，而微分环节则能预测误差的变化趋势，提前进行调整。然而，它们三者之间需要经过精细的协调才能获得最佳的控制效果。

### 2.2.2 传统PID参数计算方法

传统上，PID参数的计算依赖于经验公式或者手动调节方法。在实际应用中，工程师经常采用Ziegler-Nichols方法，该方法提供了基于系统开环传递函数的一套参数整定规则。这种方法的核心是通过开环系统的阶跃响应来估计参数值。

以下是一些基本的Ziegler-Nichols方法规则：

- **时间比例法**（Time-Proportionate Method）：该方法通过测量系统对单位阶跃输入的反应时间来计算PID参数。
- **频率响应法**（Frequency-Response Method）：通过系统的频率响应特性来推导出PID参数。

使用Ziegler-Nichols方法，首先需要识别系统的时间常数（T）和延迟时间（L）。然后按照以下公式计算出P、I、D参数的初始值：

- P参数：Kp = 1.2 * (T / L)
- I参数：Ki = 2 * Kp / T
- D参数：Kd = Kp * T / 8

需要注意的是，这些计算出的参数值只是一个起点，实际应用中，通常还需要结合系统的具体表现进行调整，以达到更好的控制效果。在MATLAB环境下，可以通过编写脚本直接计算这些参数，或者利用MATLAB自带的PID Tuner工具进行图形化的参数调整。

## 2.3 MATLAB仿真环境搭建

### 2.3.1 Simulink基础与搭建步骤

Simulink是MATLAB的一个附加产品，它提供了一个可视化的环境，允许工程师进行动态系统的建模、仿真和分析。利用Simulink，工程师可以将数学模型转换为图形模型，通过拖放组件的方式来构建复杂的控制系统。

搭建Simulink仿真环境的步骤一般如下：

1. 打开Simulink，并创建一个新的模型。
2. 在Simulink库浏览器中选择所需模块，例如信号源、控制系统组件、输出显示等。
3. 将选择的模块拖拽到模型画布上，并用线连接它们以构建完整的系统模型。
4. 双击每个模块设置参数，如PID控制器的P、I、D参数等。
5. 配置仿真参数，比如仿真时间、求解器类型等。
6. 运行仿真并观察结果。

举例来说，建立一个包含PID控制器的简单控制系统仿真模型的步骤如下：

% 在MATLAB命令窗口中
open_system(new_system('simplePID'));
add_block('simulink/Commonly Used Blocks/PID Controller', 'simplePID/PID Controller');
add_block('simulink/Sources/Step', 'simplePID/Step Input');
add_block('simulink/Sinks/Scope', 'simplePID/Scope Output');

这个过程创建了一个新的Simulink模型`simplePID`，添加了步进输入、PID控制器和示波器输出。

### 2.3.2 仿真环境的测试与验证

在仿真环境搭建完成之后，进行测试与验证是确保模型准确性的关键步骤。测试与验证的目的在于保证模型能够正确反映实际系统的动态行为，并且确保控制器性能满足预期。

仿真的基本流程包括：

1. **模型的静态测试**：检查系统模型的所有连接是否正确，参数设置是否合理。
2. **运行仿真**：观察系统输出是否符合预期，是否出现了意外的动态响应。
3. **参数调整**：若仿真结果不理想，可能需要调整模型参数或者控制策略。
4. **动态响应分析**：分析系统对特定输入（如阶跃信号、脉冲信号等）的响应，确保系统的稳定性和性能指标。

在MATLAB中，可以利用Simulink模型的`Scope`和`To Workspace`等模块来观察和记录仿真结果。对于控制器参数的验证，可以使用`PID Tuner`工具进行自动调整，也可以手动调整参数，观察系统性能的变化。

测试与验证工作并不是一次性的，在控制器设计和系统优化的过程中，需要不断重复进行仿真测试和参数调整，以达到最佳的控制效果。

# 3. PID控制器的MATLAB实践应用

## 3.1 基于MATLAB的PID控制器仿真

### 3.1.1 单回路系统的PID控制仿真示例

在进行PID控制器的仿真时，MATLAB提供了一个非常强大的工具Simulink。Simulink是一个基于图形界面的仿真工具，它允许用户通过拖放不同的功能模块来快速构建系统模型，并对系统进行动态仿真。

在这个单回路系统的仿真示例中，我们将建立一个简单的反馈控制系统，使用一个典型的对象进行控制。该对象可以是一个电机、一个温度控制系统，或者任何其他具有动态响应的物理系统。以下是构建PID控制仿真模型的基本步骤：

1. 打开Simulink，并创建一个新的模型。
2. 从Simulink的库中拖入所需的模块，这通常包括：
- 参考信号（例如阶跃输入或正弦波信号）
- PID控制器模块
- 被控对象模型（可以使用传递函数、状态空间等表示）
- 测量装置（例如传感器）
- 作用元件（例如电机驱动器）
- 示波器用于观察输出响应
3. 将这些模块通过信号线连接起来，形成一个闭环控制系统。
4. 双击PID控制器模块，输入适当的PID参数（比例、积分和微分）。
5. 配置好模拟的时间长度，开始仿真。

以一个简单的一阶加时滞对象为例，其传递函数可以表示为：

\[ G(s) = \frac{K}{Ts+1}e^{-Ls} \]

其中，\(K\)是增益，\(T\)是时间常数，\(L\)是时滞。通过Simulink建立模型并添加PID控制器模块后，我们可以开始调整PID参数来观察系统的响应。

该示例中，一个简单的阶跃输入将被应用到系统中，通过调节PID参数，我们可以看到系统输出的响应变化。Simulink中还包含了一个自动调节工具，如PID Tuner，它可以帮助我们自动选择合适的PID参数以达到最佳的系统性能。

### 3.1.2 多输入多输出（MIMO）系统的PID控制仿真示例

多输入多输出（MIMO）系统中的PID控制相较于单回路系统更为复杂，因为需要同时考虑多个输入和输出信号。在MATLAB中，使用Simulink进行MIMO系统的PID仿真，可以按照以下步骤：

1. 打开Simulink并创建一个新的模型。
2. 根据MIMO系统的特点，拖入相应数量的PID控制器模块。
3. 根据系统的结构，连接好各个控制回路。
4. 使用Simulink中的库函数来描述各个