MATLAB控制系统MIMO系统分析与控制器设计：掌握多输入多输出控制的精髓

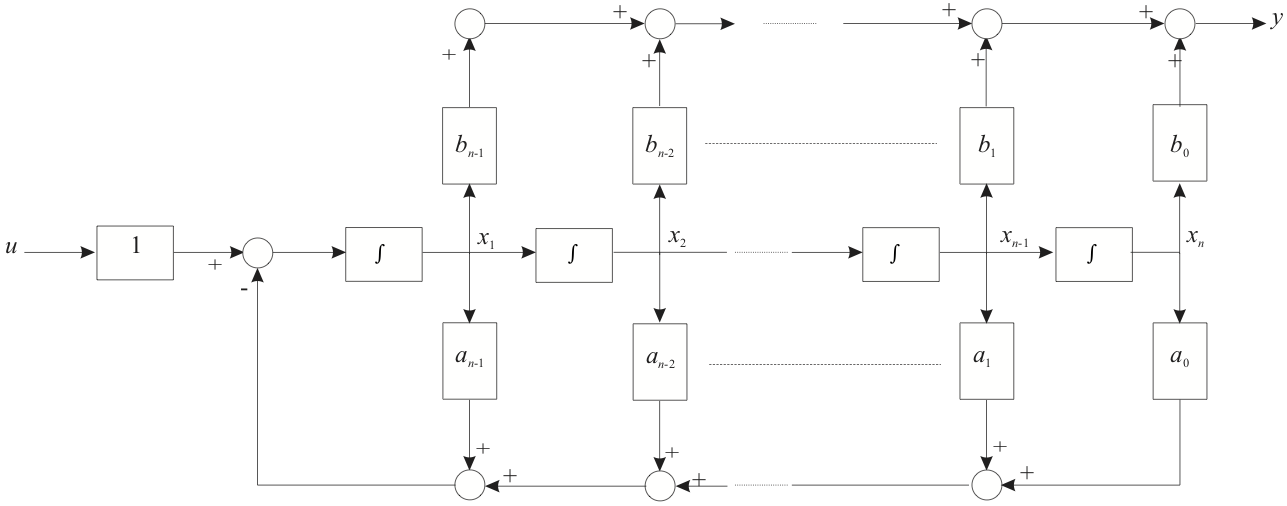
# 1. MATLAB控制系统概述

MATLAB是一种广泛应用于工程计算和算法开发的高级编程环境，尤其在控制系统领域，它提供了强大的工具和函数库，以便于控制系统的设计、仿真和分析。通过MATLAB，工程师和研究人员能够构建数学模型，模拟控制系统的动态行为，并对系统的性能进行评估和优化。

控制系统作为工程领域的一个重要分支，它涉及到各种领域，如机器人技术、航空航天、自动化过程控制等。控制系统的核心目标是确保系统行为与预期目标一致，这涉及到对系统状态的精确感知和控制。

在MATLAB中，控制系统工具箱（Control System Toolbox）提供了设计、分析和模拟线性和非线性系统所需的基本工具。无论是简单的单输入单输出（SISO）系统还是复杂的多输入多输出（MIMO）系统，MATLAB都能够提供全面的建模、分析和设计解决方案。

# 2. 多输入多输出（MIMO）系统的基础理论

### 2.1 MIMO系统的定义与特性

#### 2.1.1 MIMO系统的概念解析
多输入多输出（MIMO）系统指的是在控制系统中，存在多个输入信号和多个输出信号的系统。与传统的单输入单输出（SISO）系统相比，MIMO系统可以提供更高的性能和灵活性。在航空、航天、通信、机器人学和其他高科技领域中，MIMO技术因其能够提高系统效率、提升数据传输速率以及增强信号抗干扰能力而被广泛应用。

MIMO系统的关键之处在于其可以同时处理多个信号，这就需要复杂的信号处理和控制算法来确保各个通道之间不会相互干扰。MIMO技术的另一个优势是能够利用空间多样性，通过多个天线实现数据的并行传输。

#### 2.1.2 MIMO系统的数学模型
MIMO系统的数学模型通常涉及矩阵代数，以描述不同输入与输出之间的相互作用。一个简单的MIMO系统的线性模型可以用以下方程表示：

\[ \mathbf{Y}(s) = \mathbf{G}(s) \mathbf{U}(s) \]

其中，\(\mathbf{Y}(s)\)表示输出信号向量的拉普拉斯变换，\(\mathbf{U}(s)\)是输入信号向量的拉普拉斯变换，而\(\mathbf{G}(s)\)是系统传递函数矩阵。传递函数矩阵中的每个元素代表了单个输入通道与输出通道之间的传递函数。

### 2.2 MIMO系统的传递函数与状态空间表示

#### 2.2.1 传递函数矩阵的基础
传递函数矩阵是分析线性MIMO系统的核心工具。在MATLAB中，可以使用`tf`函数创建传递函数对象，并用矩阵方式表示多个输入和输出之间的关系。下面是一个简单的MIMO系统传递函数矩阵创建的例子：

num = {[1 3], [2 4]; [0 5 1], [1 6]}; % 分子多项式系数，两个输入两个输出
den = {[1 7 2], [3 8]; [1 9 4], [2 10]}; % 分母多项式系数
G = tf(num, den); % 创建传递函数矩阵

在上述代码中，`num`和`den`是定义系统传递函数矩阵分子和分母的多项式系数矩阵。通过这种方式，我们能够以矩阵形式处理MIMO系统的多个输入和输出。

#### 2.2.2 状态空间模型的建立与转换
状态空间模型提供了一种描述系统动态行为的方法，更适合于复杂系统的分析和设计。对于MIMO系统，状态空间模型可以表示为：

\[ \mathbf{\dot{x}}(t) = \mathbf{A}\mathbf{x}(t) + \mathbf{B}\mathbf{u}(t) \]
\[ \mathbf{y}(t) = \mathbf{C}\mathbf{x}(t) + \mathbf{D}\mathbf{u}(t) \]

其中，\(\mathbf{x}(t)\)是状态向量，\(\mathbf{u}(t)\)是输入向量，\(\mathbf{y}(t)\)是输出向量，\(\mathbf{A}\)是系统矩阵，\(\mathbf{B}\)是输入矩阵，\(\mathbf{C}\)是输出矩阵，\(\mathbf{D}\)是直接传递矩阵。状态空间模型可以利用MATLAB中的`ss`函数来建立：

A = [ -3 1; 0 -5 ];
B = [ 1; 2 ];
C = [ 1 0 ];
D = 0;
sys = ss(A, B, C, D); % 创建状态空间模型

### 2.3 MIMO系统的稳定性和性能指标

#### 2.3.1 系统稳定性判据
MIMO系统的稳定性判定是控制系统设计中的一个核心问题。一般而言，一个线性时不变（LTI）系统被认为是稳定的，如果它的所有极点都有负的实部。在MATLAB中，可以通过计算系统矩阵的特征值来判断MIMO系统的稳定性：

eigenvalues = eig(A); % 计算系统矩阵A的特征值
if all(real(eigenvalues) < 0)
    disp('系统是稳定的');
else
    disp('系统是不稳定的');
end

#### 2.3.2 性能指标的量化方法
性能指标用于衡量系统对于某些输入信号的响应品质，如快速性、准确性、鲁棒性等。对于MIMO系统，可以使用超调量、上升时间、峰值时间、调整时间等指标。在MATLAB中，可以使用`stepinfo`函数来获取并量化这些性能指标：

info = stepinfo(sys); % 获取系统阶跃响应信息
disp(info);

在上述代码中，`stepinfo`函数计算了系统的性能指标，并将其存储在`info`变量中。通过查看`info`的内容，我们可以了解系统的快速性、准确性等特性。

总结上文，本章节详细探讨了MIMO系统的定义、特性和数学模型，并着重介绍了传递函数矩阵和状态空间模型的建立方法。我们还涉及了如何利用MATLAB来判定系统稳定性及量化性能指标。这些基础理论是深入理解并应用MIMO系统的关键，对于控制系统的设计和分析尤为重要。在后续章节中，我们将继续深入探讨MIMO系统在MATLAB中的具体应用，以及如何使用MATLAB进行系统建模、分析和优化。

# 3. MATLAB在MIMO系统分析中的应用

## 3.1 使用MATLAB进行系统建模

### 3.1.1 MATLAB中的控制系统工具箱

MATLAB提供了强大的控制系统工具箱，专门用于分析、设计以及模拟控制系统。这个工具箱中包含了多种函数和命令，可以让用户方便地进行系统建模、时域和频域分析，以及设计控制器等。控制系统工具箱包括但不限于传递函数、状态空间模型、零极点分析以及响应分析等，这些都为工程师和研究者提供了便捷的工作流程。

一个控制系统工具箱中的基本函数包括 `tf`、`ss`、`zpk` 等，它们分别用于创建传递函数模型、状态空间模型以及零极点增益模型。通过这些函数可以建立各种控制系统的数学模型，便于进一步分析。

### 3.1.2 MIMO系统建模示例与分析

考虑一个具有两个输入和两个输出的MIMO系统，我们首先用数学方程来描述其动态：

[ x1_dot ] = [ a11 a12 ] * [ x1 ] + [ b11 b12 ] * [ u1 ]
[ x2_dot ]   [ a21 a22 ]   [ x2 ]   [ b21 b22 ]   [ u2 ]

在MATLAB中，我们可以使用状态空间函数 `ss` 来定义这个系统模型：

% 定义状态空间模型矩阵
A = [a11, a12; a21, a22];
B = [b11, b12; b21, b22];
C = eye(2);
D = zeros(2, 2);

% 创建状态空间模型
MIMO_sys = ss(A, B, C, D);

一旦建立了模型，我们可以使用 `step`、`impulse` 或者 `bode` 等函数来观察系统的时间响应或者频率响应。

% 时域分析：单位阶跃响应
figure;
step(MIMO_sys);
title('MIMO System Step Response');

% 频域分析：波特图
figure;
bode(MIMO_sys);
title('MIMO System Bode Plot');

## 3.2 MIMO系统的时域和频域分析

### 3.2.1 时域响应的MATLAB仿真

时域分析是控制系统分析中的一个重要环节，它关注系统对不同输入信号的反应。MATLAB提供了多种方法来进行时域响应分析，包括单位阶跃响应、单位脉冲响应等。为了观察系统的动态特性，我们可以使用 `step` 函数来分析单位阶跃输入下的系统反应。

例如，考虑一个两输入两输出的MIMO系统，我们已经通过 `ss` 函数创建了其状态空间模型。我们可以通过下面的代码来获取并分析其单位阶跃响应。

% 假设我们已经得到了状态空间模型 MIM