数据科学中的逻辑回归：实战代码与应用详解

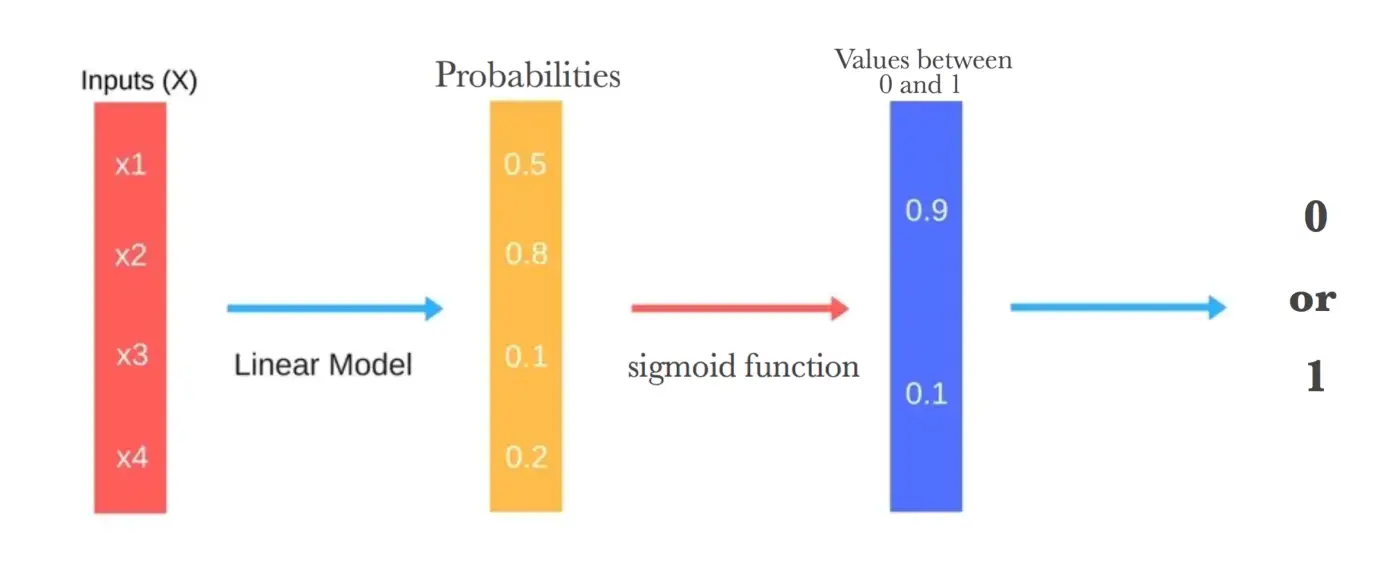
# 1. 逻辑回归简介

逻辑回归是一种广泛应用于二分类问题的统计方法，尽管名字中带有“回归”，但它实际上是用于分类问题的。它的核心思想是通过一个逻辑函数，将线性回归的输出映射到(0,1)区间，从而得到一个概率值，用于表示某个事件发生的可能性。在机器学习领域，逻辑回归因其模型简单、易于解释且计算效率高等优点，成为了数据科学家们首选的入门级算法之一。

逻辑回归模型的输出通常用于估计某件事情发生的概率，并根据预设的阈值，判断最终的分类结果。例如，在垃圾邮件识别中，逻辑回归可以输出一封邮件为垃圾邮件的概率，如果这个概率超过了一定的阈值（如0.5），则将这封邮件标记为垃圾邮件。

在数据科学领域，逻辑回归还常用于风险评估和信用评分等场景。通过对历史数据的分析，预测某件事件发生的可能性，为决策提供支持。尽管在面对复杂的非线性问题时，逻辑回归可能不如一些高级算法（如支持向量机、随机森林等）那么强大，但在理解模型基本原理、评估结果的可靠性以及快速实现业务价值方面，逻辑回归无疑是一个极佳的选择。

# 2. 逻辑回归的数学原理

### 2.1 逻辑回归模型的基本概念

逻辑回归模型是一种广泛应用于二分类问题的统计方法。它不仅能够预测某个事件发生的概率，还可以给出清晰的类别预测。

#### 2.1.1 逻辑函数与概率

逻辑回归的核心是逻辑函数，通常使用S形的sigmoid函数来定义。S形曲线可以将任意实数映射到(0,1)区间，这使得它非常适合于表示概率。

公式如下：

\[ \sigma(z) = \frac{1}{1 + e^{-z}} \]

其中，\( z \) 是线性函数 \( z = \theta^T x \)，\( \theta \) 是模型参数，\( x \) 是特征向量。通过这个函数，模型输出的是正类的概率 \( P(y=1|x; \theta) \)。

#### 2.1.2 模型参数估计与成本函数

参数估计是逻辑回归的核心环节。参数估计通常通过最大化似然函数来获得，这等价于最小化下面的成本函数（也称为交叉熵损失）：

\[ J(\theta) = - \frac{1}{m} \sum_{i=1}^{m} [y^{(i)} \log(h_\theta(x^{(i)})) + (1 - y^{(i)}) \log(1 - h_\theta(x^{(i)}))] \]

其中，\( m \) 是样本数量，\( h_\theta(x) \) 是模型对输入 \( x \) 的预测值，\( y \) 是真实标签。通过梯度下降等优化算法，可以求解出最佳参数 \( \theta \)。

### 2.2 逻辑回归的优化算法

优化算法是机器学习模型训练过程中不可或缺的组成部分，它负责在高维空间中寻找成本函数的最小值。

#### 2.2.1 梯度下降法详解

梯度下降法是最基础的优化算法，用于最小化成本函数。梯度下降的核心思想是按照成本函数的负梯度方向更新参数，直到收敛到最小值。

迭代公式为：

\[ \theta_j := \theta_j - \alpha \frac{\partial}{\partial \theta_j} J(\theta) \]

其中，\( \alpha \) 是学习率，\( \frac{\partial}{\partial \theta_j} J(\theta) \) 是成本函数关于参数 \( \theta_j \) 的梯度。

#### 2.2.2 拟牛顿法与牛顿法概述

拟牛顿法和牛顿法是梯度下降法的改进版，它们使用二阶导数（海森矩阵）来提供更快的收敛速度。拟牛顿法通过近似海森矩阵来避免直接计算二阶导数，而牛顿法则直接使用海森矩阵。

牛顿法的更新公式为：

\[ \theta := \theta - H^{-1} \nabla J(\theta) \]

其中，\( H^{-1} \) 是海森矩阵的逆矩阵，\( \nabla J(\theta) \) 是梯度向量。

### 2.3 模型评估与性能指标

模型评估是模型训练完成之后的重要步骤。通过性能指标，我们可以了解模型的分类效果。

#### 2.3.1 真正率、假正率与AUC-ROC曲线

真正率（True Positive Rate, TPR）和假正率（False Positive Rate, FPR）是评估分类模型性能的基本指标。它们描述了在不同阈值下模型分类的正确和错误情况。

AUC-ROC曲线是将真正率与假正率进行可视化的方法。AUC值越高，模型性能越好。

#### 2.3.2 模型准确度与混淆矩阵

准确度（Accuracy）是评估分类器性能的直观指标，它表示模型预测正确的样本数与总样本数的比例。

混淆矩阵（Confusion Matrix）是一个表格，用于描述分类模型的预测结果与真实情况的对比。通过混淆矩阵可以得到模型的精确度、召回率等指标。

在逻辑回归模型的训练与评估过程中，以上这些概念和方法共同构成了模型从构建到分析的完整生命周期。通过这些数学原理和评估指标，可以系统性地分析和优化逻辑回归模型，使其达到最佳性能。

# 3. 逻辑回归的实战代码

## 3.1 数据预处理与特征工程

在数据科学的实际应用中，数据预处理与特征工程是构建预测模型不可或缺的一环。这一步骤直接影响到模型的性能和最终的预测效果。逻辑回归同样遵循这一原则，接下来让我们深入探讨数据预处理与特征工程在逻辑回归中的应用。

### 3.1.1 数据清洗与标准化

数据清洗是数据预处理的基础，目的是为了去除数据中的噪声和不一致信息，保证数据的质量。具体操作包括填补缺失值、去除异常值、处理重复记录等。

import pandas as pd
from sklearn.impute import SimpleImputer
from sklearn.preprocessing import StandardScaler

# 加载数据集
data = pd.read_csv('data.csv')

# 填补缺失值
imputer = SimpleImputer(strategy='mean')
data_imputed = pd.DataFrame(imputer.fit_transform(data), columns=data.columns)

# 标准化数据
scaler = StandardScaler()
data_scaled = pd.DataFrame(scaler.fit_transform(data_imputed), columns=data.columns)

在上述代码中，`SimpleImputer` 用于处理缺失值，这里我们采用了平均值填充策略。标准化是通过对数据的均值和标准差进行调整，将数据缩放到一个新的尺度，以便于模型更好地处理数据。

### 3.1.2 特征选择与特征提取

逻辑回归模型的复杂度相对较低，因此特征选择和提取尤其重要。特征选择的目的是减少特征的数量，保留对目标变量预测能力强的特征，从而简化模型，提高预测精度。

from sklearn.feature_selection import SelectKBest, chi2

# 特征选择
X_new = SelectKBest(chi2, k=10).fit_transform(data_scaled, target)

# 查看所选特征
selected_features = data_scaled.columns[SelectKBest(chi2, k=10).get_support()]

在这段代码中，我们使用了卡方检验（`chi2`）来选择与目标变量最相关的特征。`k`参数指定了需要选择的特征数量。通过这样的方法，我们可以保留那些对预测结果有显著影响的特征。

## 3.2 逻辑回归的Python实现

逻辑回归的Python实现通常借助于`scikit-learn`库，这个库为我们提供了便捷的接口来构建和训练模型。接下来，我们将具体讲解如何使用`scikit-learn`来实现逻辑回归。

### 3.2.1 使用scikit-learn构建模型

`scikit-learn`库中的`LogisticRegression`类是构建逻辑回归模型的核心。通过调整其参数，我们可以构建出适合不同数据集的逻辑回归模型。