逻辑回归与分类：实战最佳实践与案例分析

# 1. 逻辑回归基础与分类原理

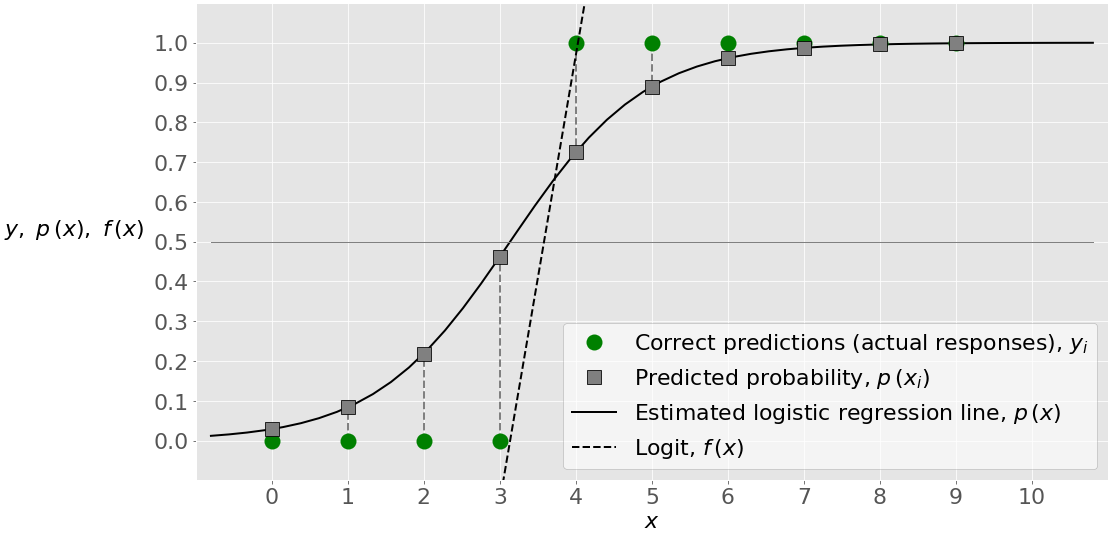
逻辑回归是一种广泛应用于分类任务的统计方法，尤其在二分类问题中表现出色。其基本思想是通过一个逻辑函数来预测某一事件发生的概率，这个函数通常采用sigmoid函数，它可以将任意值映射到(0,1)区间内，使其可以解释为概率。

逻辑回归的分类原理基于概率论中的条件概率。在处理分类问题时，模型通过学习历史数据中的特征与标签之间的关系，形成一个决策边界，将数据划分为不同的类别。这个决策边界是通过最大化训练数据的似然函数来确定的，即选择能够最好地反映数据特征的参数值。

逻辑回归的输出虽然可以看作是属于某一类的概率，但它实际上是一个线性模型。这使得它在处理某些问题时具有很好的解释性和效率。在接下来的章节中，我们将深入探讨逻辑回归的理论基础和实际应用技巧。

# 2. 逻辑回归的理论与数学模型

### 2.1 逻辑回归模型概述

逻辑回归模型是机器学习领域内应用非常广泛的分类算法，尽管名字中包含“回归”二字，但实际上它是一种分类方法。逻辑回归用于估计某个事件发生的概率，通过这个概率来判断样本属于某个类别的可能性。

#### 2.1.1 概率解释与模型推导

逻辑回归的概率解释核心在于Sigmoid函数，该函数能够将任何实数映射到(0,1)区间内，这样就将线性回归模型的输出转化为了一个概率值。Sigmoid函数的定义如下：

import numpy as np
import matplotlib.pyplot as plt

def sigmoid(z):
    return 1 / (1 + np.exp(-z))

接下来，我们将Sigmoid函数应用在线性回归的预测值上，得到一个概率估计。具体来说，如果我们有特征向量x，和参数向量θ，线性回归模型预测的分数是θTX。Sigmoid函数将这个分数转化为概率值：

def logistic_regression_score(x, theta):
    return sigmoid(np.dot(x, theta))

通过设定阈值（通常是0.5），我们能够把概率转化为类别标签，例如，如果概率大于0.5则判断为类别1，否则为类别0。这种概率化的解释让逻辑回归在处理二分类问题时具有非常直观的解释性。

#### 2.1.2 损失函数与优化算法

逻辑回归的损失函数是交叉熵损失（Cross-Entropy Loss）。在二分类情况下，损失函数可以表示为：

def log_loss(y, y_hat):
    return - np.mean(y * np.log(y_hat) + (1 - y) * np.log(1 - y_hat))

这里的y是真实的标签，y_hat是模型预测的概率。优化算法通常采用梯度下降法来最小化损失函数。每一步梯度下降都会更新参数θ，更新公式如下：

def gradient_descent(x, y, theta, alpha):
    m = len(y)
    y_hat = logistic_regression_score(x, theta)
    gradient = np.dot(x.T, (y_hat - y)) / m
    theta = theta - alpha * gradient
    return theta

其中，alpha是学习率。通过迭代更新参数，直到损失函数收敛或者达到预定的迭代次数。

### 2.2 模型的统计学习理论

#### 2.2.1 最大似然估计与参数估计

逻辑回归模型参数θ的估计采用最大似然估计（Maximum Likelihood Estimation, MLE）方法。通过最大化数据的似然函数来估计θ，似然函数表达了观测到当前数据的概率。

def log_likelihood(x, y, theta):
    return np.sum(y * np.log(logistic_regression_score(x, theta)) + 
                  (1 - y) * np.log(1 - logistic_regression_score(x, theta)))

在逻辑回归模型中，通常通过求导数等于零来找到使似然函数最大的参数θ。实际上，这等价于最小化负对数似然函数，即我们之前讨论的交叉熵损失函数。

#### 2.2.2 模型的评估与检验

评估逻辑回归模型通常使用混淆矩阵（Confusion Matrix）和接收者操作特征曲线（ROC curve）以及其下的面积（AUC）作为指标。混淆矩阵给出了模型预测的真正例、假正例、真负例和假负例的数量，AUC则是在所有可能的分类阈值下模型预测正类的准确性的一个整体评估。

### 2.3 逻辑回归的正则化技术

#### 2.3.1 过拟合问题及其解决方案

过拟合是机器学习模型学习到了训练数据中的噪声和异常值，导致模型在新的数据上泛化能力差。逻辑回归通过引入正则化项来避免过拟合，例如L1正则化（Lasso回归）和L2正则化（Ridge回归）。

def regularized_logistic_regression_score(x, theta, lambda_, type="L2"):
    if type == "L1":
        return sigmoid(np.dot(x, theta) - lambda_ * np.abs(theta))
    else: # L2
        return sigmoid(np.dot(x, theta) - lambda_ * theta**2)

在L1正则化下，一些参数可能会被缩减到0，这有助于特征选择；而在L2正则化下，所有参数会被缩减，但是不会缩减到0，这样可以控制模型的复杂度，而不会产生稀疏解。

#### 2.3.2 L1与L2正则化深入剖析

L1正则化可以产生稀疏模型，因为某些参数会被正则化到0，这种特性使得L1正则化在特征选择中非常有用。L2正则化是所有参数的平方和乘以一个系数，目的是让大的参数变得更小，这有助于平滑模型。

def l1_regularization(theta, lambda_):
    return np.sum(np.abs(theta)) * lambda_

def l2_regularization(theta, lambda_):
    return np.sum(theta**2) * lambda_

在实践中，通常采用交叉验证的方法来确定最优的正则化系数lambda_，选择一个既能防止过拟合又不过度限制模型能力的lambda_值。

### 章节小结

逻辑回归的理论与数学模型是理解和应用逻辑回归算法的基础。本章节首先介绍了逻辑回归模型的概率解释和数学推导，然后探讨了模型的统计学习理论，包括参数估计和模型评估方法。接着，我们分析了过拟合问题及其通过正则化技术进行解决的方法，深入剖析了L1和L2正则化的不同应用场景和特点。逻辑回归作为机器学习领域内应用广泛的经典算法，其在实际应用中依然扮演着重要角色，尤其是在需要模型具有良好解释性的情景中。本章节为我们深入理解逻辑回归模型及其背后的数学原理奠定了坚实的基础，下一章节将进一步探讨如何在分类任务中应用逻辑回归，并介绍实践中的一些技巧和最佳实践。

# 3. 逻辑回归在分类中的实践技巧

逻辑回归作为经典的分类算法之一，其实践技巧对于数据科学家和机器学习工程师而言是必备知识。本章将深入探讨如何在数据预处理、模型训练、参数调优以及模型评估等环节中运用逻辑回归，并提供相