逻辑回归的在线学习：增量学习与数据流处理技巧

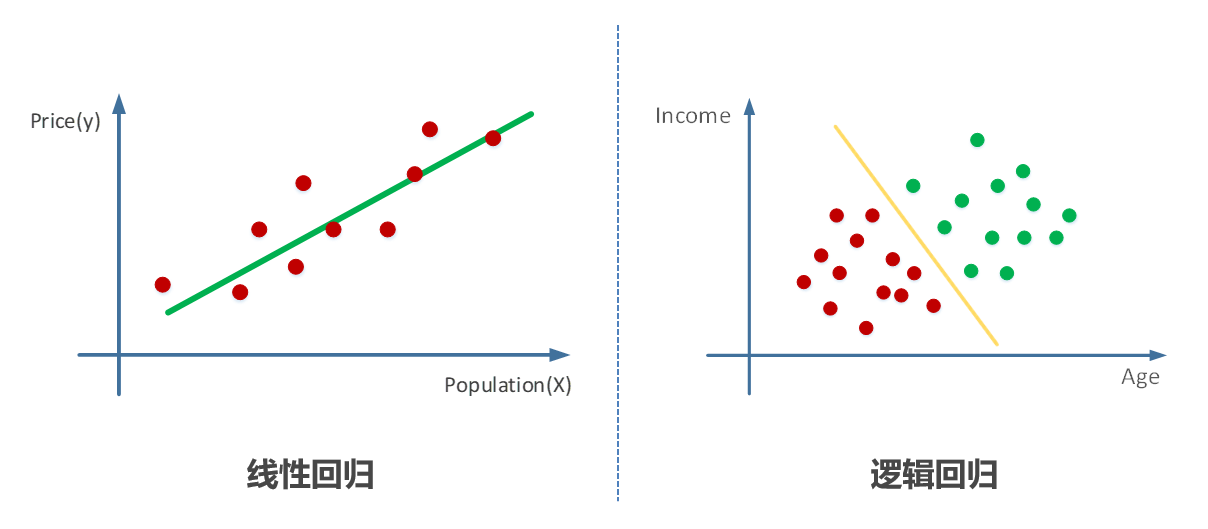
# 1. 逻辑回归简介与在线学习概念

在当今的数据驱动时代，逻辑回归作为一种基础而强大的统计工具，被广泛应用于分类问题中，尤其是在在线学习的场景下。逻辑回归不仅能够预测目标变量是正类的概率，还具有模型简洁、易于理解和实施的特点。在线学习是机器学习中的一个分支，其核心在于通过实时或近实时地从数据流中学习，使模型能够迅速适应数据的变化，这在动态环境和实时数据分析中具有重大意义。

接下来，我们将深入探讨逻辑回归的基本概念、如何处理在线学习环境下的数据流，以及相关工具和实践技巧。首先，我们将从逻辑回归的基础知识开始，理解它如何在不同领域中作为分类器使用，并且逐渐引出在线学习的概念，为后续章节的高级内容打下基础。

逻辑回归模型在处理大规模数据流时，通常会采用在线学习或增量学习的方式，这意味着模型参数在接收到新数据时实时更新，而不是重新训练整个模型。这种方式特别适合于数据不断到来且需要即时响应的场景，如实时广告投放、金融风控、社交网络内容推荐等。

# 一个简单的逻辑回归模型示例代码
from sklearn.linear_model import LogisticRegression

# 创建逻辑回归实例
log_reg = LogisticRegression()

# 训练模型（以示例数据集为例）
# X_train, y_train为训练数据和标签，此处省略具体数据
log_reg.fit(X_train, y_train)

# 使用模型进行预测
# X_new为新数据实例
predictions = log_reg.predict(X_new)

在这个例子中，我们使用了sklearn库中的逻辑回归类进行模型训练和预测，该过程在有新数据到来时可以重复执行，以实现实时学习的效果。逻辑回归模型的简单性和在处理在线数据流方面的灵活性，使得它成为了机器学习领域的一个重要工具。

# 2. 逻辑回归模型与增量学习理论

## 2.1 逻辑回归模型的数学基础

### 2.1.1 逻辑回归的损失函数和决策边界

逻辑回归是一种广泛用于二分类问题的监督学习算法。它的模型形式是通过概率来表示一个事件发生的可能性，使用sigmoid函数将线性回归的输出映射到(0,1)区间内，从而得到类别概率：

import numpy as np

def sigmoid(z):
    return 1 / (1 + np.exp(-z))

z = np.linspace(-10, 10, 100)
y = sigmoid(z)

# 绘制sigmoid函数图形
import matplotlib.pyplot as plt
plt.plot(z, y)
plt.xlabel('z')
plt.ylabel('sigmoid(z)')
plt.title('Sigmoid Function in Logistic Regression')
plt.show()

在逻辑回归中，损失函数通常使用对数损失（log loss）：

def log_loss(y_true, y_pred):
    return -np.mean(y_true * np.log(y_pred) + (1 - y_true) * np.log(1 - y_pred))

# 假设真实标签y_true和预测概率y_pred
y_true = np.array([1, 0, 1, 1, 0])
y_pred = np.array([0.9, 0.1, 0.8, 0.7, 0.2])
print("Logistic Loss: ", log_loss(y_true, y_pred))

决策边界是模型预测概率为0.5的点。对于线性回归模型z = w^T x + b，决策边界是w^T x + b = 0的点集。当特征增加时，决策边界会变得复杂，可以是线性的也可以是非线性的。

### 2.1.2 正则化对模型复杂度的影响

正则化是防止模型过拟合的一种常用技术，它可以限制模型的复杂度。逻辑回归常用的正则化技术包括L1正则化（Lasso）和L2正则化（Ridge）：

def regularized_loss(y_true, y_pred, weights, reg_type='l2', alpha=0.1):
    """
    计算带正则化的对数损失
    """
    if reg_type == 'l1':
        reg_loss = alpha * np.sum(np.abs(weights))
    else:
        reg_loss = alpha * np.sum(np.square(weights))
    return -np.mean(y_true * np.log(y_pred) + (1 - y_true) * np.log(1 - y_pred)) + reg_loss

# 假设权重weights
weights = np.array([0.5, -0.3, 0.2])
print("Regularized Logistic Loss with L2: ", regularized_loss(y_true, sigmoid(np.dot(X, weights)), weights))

L1正则化倾向于产生稀疏权重矩阵，从而可以用来做特征选择。L2正则化倾向于使权重均匀分布，可以缓解共线性问题。

## 2.2 增量学习的原理与方法

### 2.2.1 增量学习的定义及其必要性

增量学习，又称为在线学习，是机器学习中处理数据流的一种策略，特别是在数据到达顺序有时间依赖时。它允许模型在接收到新数据后，持续不断地学习，而无需从头开始训练。这种方法对于处理大规模、实时或非静态数据非常重要。

### 2.2.2 在线学习算法的种类与选择

在线学习算法可以根据学习策略进行分类，常见的有：

- ** стохастические градиенты下降 (SGD)**: 每次迭代使用一个样本计算梯度。
- ** мини-批量 градиентного спуска (Mini-batch)**: 每次迭代使用一小批量样本来计算梯度。
- **增量支持向量机 (Incremental SVM)**: 适用于分类问题，尤其是SVM。
- ** персептрон**: 在线版本的感知器模型，适合二分类问题。

选择合适的在线学习算法依赖于具体的应用场景、数据特性和资源限制。

### 2.2.3 增量学习与传统批量学习的比较

增量学习与传统批量学习的主要区别在于数据处理方式和模型更新策略。批量学习在训练时需要整个数据集，模型更新时需要重新训练。而增量学习一次只处理少量数据，模型更新是连续的，更为高效和灵活。

## 2.3 增量学习中的优化技巧

### 2.3.1 梯度更新策略

在增量学习中，梯度更新策略是核心问题之一。SGD是一种常用的梯度更新策略，它在每次迭代中更新模型参数：

def sgd(X, y_true, weights, learning_rate=0.01):
    """
    使用随机梯度下降法更新权重
    """
    m = len(y_true)
    grad = sigmoid(np.dot(X, weights)) - y_true
    weights -= learning_rate * np.dot(X.T, grad) / m
    return weights

### 2.3.2 避免过拟合与模型更新

为了防止过拟合，可以使用L1/L2正则化。模型更新时，还可以通过逐步遗忘旧数据的影响，或者使用滑动窗口机制来实现对新数据的敏感度调整。这样模型可以更快地适应新趋势，同时保留历史知识。

增量学习为持续学习提供了可能，使模型得以适应动态变化的数据环境，提高机器学习的效率和效果。在下一章中，我们将深入探讨数据流处理与逻辑回归的实践应用。

# 3. 数据流处理与逻辑回归实践

## 3.1 数据流的特点与处理策略

### 3.1.1 数据流的特性

数据流是源源不断地产生和流动的数据的集合，它们具有高流量、实时性、无限性和潜在的异构性等特性。在处理数据流时，常见的挑战包括如何高效地捕捉这些数据、如何实时处理快速到达的数据以及如何从这种持续变化的数据中提取有价值的信息。

数据流与传统的批量数据处理有所不同，传