集成学习新境界：逻辑回归的Bagging和Boosting策略

# 1. 集成学习和逻辑回归的基础

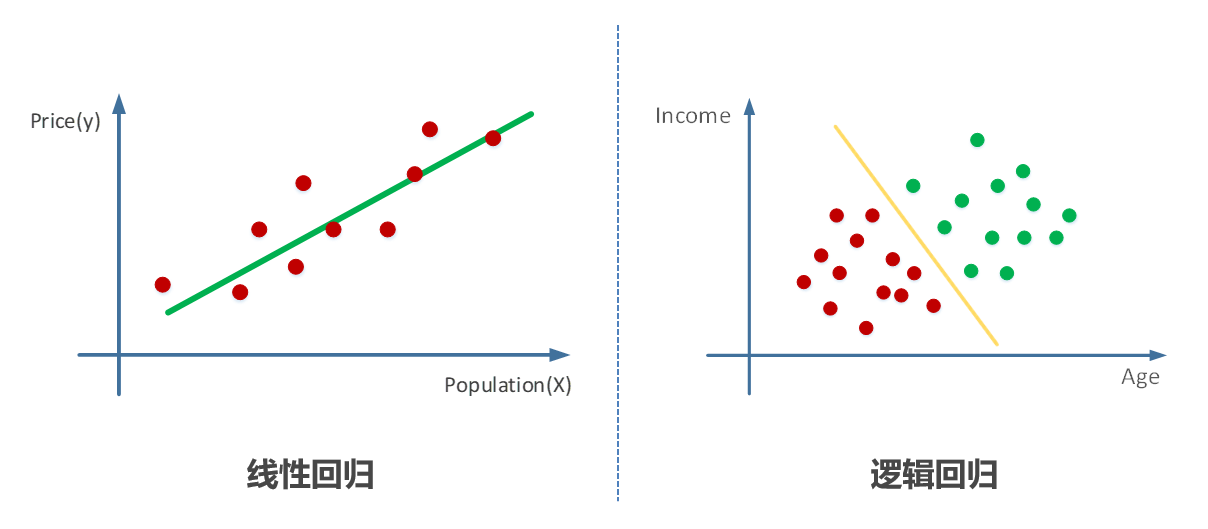
逻辑回归和集成学习是机器学习领域中两个重要的概念。逻辑回归是最简单的机器学习算法之一，主要应用于二分类问题。它基于sigmoid函数，将特征向量映射到[0,1]区间，预测结果为属于某一类别的概率。

集成学习通过构建并结合多个学习器来完成学习任务，目的是提升整体模型的性能。其中，Bagging和Boosting是两种常见的集成策略，它们分别从不同角度解决机器学习中的过拟合问题，提升模型的泛化能力。

在深入探讨逻辑回归与集成学习的结合之前，我们需要先了解逻辑回归的基本原理、其优缺点以及它是如何处理分类问题的。我们将从逻辑回归模型的构建开始，逐步介绍其数学原理，并展示如何使用逻辑回归解决实际问题。这将为我们理解集成学习策略在逻辑回归中的应用打下坚实的基础。

# 2. 逻辑回归的Bagging策略

在第一章中，我们对集成学习和逻辑回归的基本概念进行了初步的探讨。逻辑回归作为一种广泛使用的分类算法，它的稳定性、简单性和易于理解的特点使其成为许多数据科学家的首选。但是，单个模型的性能通常受到数据噪声和过拟合的影响。为了克服这些问题，我们可以将Bagging策略引入到逻辑回归模型中。本章将深入探讨Bagging的理论基础以及它在逻辑回归中的实际应用。

## 2.1 Bagging的基本原理

### 2.1.1 Bagging的理论基础

Bagging（Bootstrap Aggregating）是集成学习中一种减少泛化误差的技术，由Leo Breiman于1996年提出。其核心思想是通过结合多个模型来提高泛化性能。Bagging通过自助采样（bootstrap sampling）的方式，从原始数据集中重复抽样，创建多个子集，然后分别在每个子集上训练模型，并将这些模型的预测结果进行汇总以产生最终预测。

Bagging能够显著减少模型方差，当各个模型之间具有较低的相关性时效果最佳。因此，Bagging尤其适用于决策树这类方差较大的模型。然而，逻辑回归作为一种线性模型，其方差本身相对较低，Bagging策略仍然能够提升其稳定性和准确性，尤其是在面对含有噪声的数据集时。

### 2.1.2 Bagging在逻辑回归中的应用

在逻辑回归中应用Bagging，我们通常会创建多个逻辑回归模型，每个模型在由原始数据集抽样得到的不同子集上进行训练。然后，通过投票（分类问题）或者平均（回归问题）的方式整合各个模型的预测结果。这种策略可以帮助改善逻辑回归模型对异常值的敏感度，并提高在新数据上的预测性能。

具体操作步骤如下：

1. 对原始数据集进行多次自助采样，每次采样都得到一个大小与原始数据集相同的样本集，但样本之间允许重复，且每个样本集之间相互独立。
2. 在每个样本集上训练一个逻辑回归模型。
3. 对于新的数据点，通过所有训练好的模型进行预测，最后综合这些预测结果（在分类问题中，通常是投票法）得到最终预测。

## 2.2 Bagging的实践应用

### 2.2.1 实践案例分析

在实际的机器学习项目中，我们可以使用像Python的scikit-learn这样的库来简化Bagging策略在逻辑回归中的应用过程。以下是一个简单的实践案例，展示了如何使用scikit-learn对逻辑回归模型应用Bagging。

from sklearn.datasets import make_classification
from sklearn.linear_model import LogisticRegression
from sklearn.ensemble import BaggingClassifier
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score

# 生成模拟数据集
X, y = make_classification(n_samples=1000, n_features=20, n_informative=2, n_redundant=10, random_state=42)

# 分割数据集为训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

# 创建逻辑回归模型
logistic_model = LogisticRegression()

# 创建Bagging逻辑回归集成模型
bagging_model = BaggingClassifier(base_estimator=logistic_model, n_estimators=10, random_state=42)

# 训练模型
bagging_model.fit(X_train, y_train)

# 进行预测
predictions = bagging_model.predict(X_test)

# 计算并输出准确率
print(f"Accuracy of the Bagging model: {accuracy_score(y_test, predictions):.4f}")

在这段代码中，我们首先导入了必要的库和函数，然后创建了一个模拟的分类数据集。之后，我们将数据集分为训练集和测试集，并初始化了一个逻辑回归模型和一个包含10个逻辑回归模型的Bagging集成模型。训练完成后，我们使用测试集数据进行了预测，并计算了准确率。

### 2.2.2 实践中的问题和解决方案

在应用Bagging策略时，我们可能会遇到以下几个问题：

1. **过拟合**：虽然Bagging可以减少方差，但如果单个模型过拟合，则集成模型也可能过拟合。解决方案是调整模型的复杂度或增加更多的模型到集成中。

2. **计算成本**：训练多个模型会增加计算成本。对此，可以使用并行处理或者分布式计算来加速模型训练过程。

3. **预测时间**：集成模型的预测时间会比单个模型要长。可以通过模型简化、剪枝等技术来优化。

4. **内存消耗**：存储多个模型会占用更多内存。解决方法包括优化存储结构或采用压缩技术减少内存使用。

针对这些问题，我们可以通过调整模型参数、选择合适的硬件和软件优化来提升效率。在实践中，这些策略可以帮助我们更好地利用Bagging提升逻辑回归模型的性能。

## 2.3 Bagging集成中模型的统计分析

对于逻辑回归的Bagging集成，我们可以使用一些统计量来评价模型的性能和稳定性。以下是一些常用的统计分析方法：

- **平均准确率**：计算集成模型在测试集上的平均准确率，以评估模型整体的性能。

- **标准差**：统计集成中各个模型准确率的标准差，用于评价模型之间的稳定性差异。

- **置信区间**：计算准确率的置信区间，可以得到模型性能的可靠估计范围。

### 2.3.1 实际操作

在Python中，我们可以编写一些额外的代码来计算这些统计量。

import numpy as np

# 假设我们已经有了一系列模型的准确率
accuracies = np.array([0.85, 0.87, 0.86, 0.84, 0.88, 0.83, 0.85, 0.86, 0.85, 0.87])

# 计算平均准确率
mean_accuracy = np.mean(accuracies)

# 计算标准差
std_deviation = np.std(accuracies, ddof=1)

# 计算95%置信区间
n = len(accuracies)
standard_error = std_deviation / np.sqrt(n)
confidence_interval = (mean_accuracy - 1.96 * standard_error, mean_accuracy + 1.96 * standard_error)

print(f"Mean Accuracy: {mean_accuracy:.4f}")
print(f"Standard Deviation: {std_deviation:.4f}")
print(f"95% Confidence Interval: {confidence_interval}")

通过执行上述代码，我们得到了集成模型的平均准确率、标准差和置信区间，这些可以帮助我们对模型性能有一个全面的认识。

## 2.4 实践中的模型评估和选择

在实际的模型开发过程中，评估和选择合适的集成模型是至关重要的。这通常涉及以下几个方面：

- **交叉验证**：通过交叉验证的方法来评估模型的泛化能力。

- **模型选择**：在多个集成模型之间选择表现最好的模型。

### 2.4.1 交叉验证

交叉验证是一种统计学方法，通过将数据集分成k个子集，轮流将k-1个子集用于训练，剩下的一个子集用于验证，以此来评估模型的性能。在逻辑回归的Bagging集成中，可以采用交叉验证来更准确地估计模型的泛化误差。

### 2.4.2 模型选择

在模型选择方面，我们可以使用不同的评价指标来辅助决策，例如准确率、召回率、F1分数以及ROC-AUC值等。这些指标可以帮助我们从不同的角度来理解模型的性能。

在下一章中，我们将探讨逻辑回归的另一集成策略——Boosting，并对比这两种方法在理论和实践上的异同。

# 3. 逻辑回归的Boosting策略

#### 3.1 Boosting的基本原理

##### 3.1.1 Boosting的理论基础

Boosting是一种集成学习方法，旨在通过组合多个弱学习器来构建一个强大的集成模型。它是一种逐步算法，每一步都选择一个模型，重点学习之前模型预测错误的样本。Boosting的主要思想是将多个弱分类器进行线性组合，最终形成一个强分类器。

Boosting方法的核心在于权重的调整，每当一个模型在训练过程中出现错误时，错误的样本的权重会被增大，而正确分类的样本的权重则会减小。这样，在下一轮的模型训练中，模型会更加关注那些之前被错分的样本，逐渐提高模型的性能。

##### 3.1.2 Boosting在逻辑回归中的应用

在逻辑回归中，Boosting通常采用的是AdaBoost（Adaptive Boosting）算法。AdaBoost通过调整每个样本的权重，使得模型能够逐步提高对困难样本的识别能力。逻辑回归的输出是属于某类的概率估计，AdaBoost可以利用这个概率来调整样本权重，并作为后续模型训练的基础。

在