选择Keras损失函数：误差度量与任务匹配的技巧

# 1. Keras损失函数简介

在深度学习的领域，损失函数是衡量模型预测与真实值之间差异的指标。在Keras框架中，损失函数是构建神经网络不可或缺的一部分，它不仅帮助我们评估模型性能，还是训练过程中指导参数调整的依据。本章将简要介绍损失函数的概念和在Keras中的基础应用。

## 什么是损失函数？

损失函数（Loss Function），也称代价函数（Cost Function），用于衡量模型预测值与实际值之间的误差大小。损失函数的计算结果表明了当前模型的性能好坏，是优化算法（如梯度下降）的“指南针”。

## 损失函数的重要性

在机器学习和深度学习中，损失函数的重要性体现在以下几个方面：
1. 它直接决定了训练过程中优化算法的搜索方向；
2. 损失函数的选择会影响到模型的泛化能力；
3. 通过损失函数的值，我们能够了解模型的学习进度和效果。

## 在Keras中使用损失函数

在Keras中，损失函数通常以函数或字符串的形式作为模型编译步骤中的参数传入。例如，对于一个简单的回归问题，我们可以使用均方误差（MSE）作为损失函数：

from keras import models, layers
from keras.losses import mean_squared_error

model = models.Sequential([
    layers.Dense(64, activation='relu', input_shape=(input_shape,)),
    layers.Dense(1)
])

model.compile(optimizer='rmsprop',
              loss=mean_squared_error,
              metrics=['mae'])

在这个例子中，`mean_squared_error` 函数作为损失函数被使用，模型将会在训练过程中最小化这个损失值。通过本章的介绍，读者将对Keras中的损失函数有一个初步的了解，并为深入学习后续章节奠定基础。

# 2. 理解损失函数背后的理论

### 2.1 损失函数在机器学习中的作用

损失函数是衡量模型预测值与真实值之间差异的重要工具，它在机器学习模型的训练过程中扮演着核心角色。理解损失函数的作用对于构建有效的机器学习系统至关重要。损失函数不仅能帮助我们理解模型当前的性能，还能够提供优化模型的线索。

#### 2.1.1 损失函数与优化算法的关系

在机器学习中，模型的训练过程本质上是一个优化问题，而损失函数则定义了优化的目标。优化算法如梯度下降法，正是通过最小化损失函数来更新模型参数，逐步使模型拟合训练数据的过程。因此，损失函数与优化算法之间存在着密切的联系。损失函数的梯度告诉我们损失函数相对于模型参数的变化方向和幅度，优化算法正是利用这些梯度信息来指导参数的更新。

# 示例：在Keras中使用梯度下降优化器来最小化损失函数

# 导入必要的库
from keras.models import Sequential
from keras.layers import Dense
from keras.optimizers import SGD

# 创建模型
model = Sequential()
model.add(Dense(64, activation='relu', input_shape=(input_dim,)))
model.add(Dense(1, activation='linear'))

# 编译模型，使用SGD优化器和均方误差损失函数
model.compile(optimizer=SGD(), loss='mse')

# 模型开始训练
model.fit(x_train, y_train, epochs=50, batch_size=32)

#### 2.1.2 损失函数的选择对模型的影响

不同的任务和数据特性需要不同的损失函数。选择合适的损失函数对模型的性能和训练过程都有显著的影响。例如，在回归任务中，均方误差（MSE）是常用的损失函数，因为它的数学特性适合连续值预测。而在分类问题中，交叉熵损失函数则更为常见，因为其能够更好地反映概率分布之间的差异。

### 2.2 常见的损失函数类型及其应用场景

#### 2.2.1 均方误差（MSE）和均方根误差（RMSE）

均方误差（MSE）是预测值与实际值差的平方的平均值，而均方根误差（RMSE）是MSE的平方根。MSE对大误差的惩罚更大，因其取平方值，因此在回归任务中应用广泛。

graph LR
A[MSE计算公式] --> B[计算每个点的误差平方]
B --> C[对所有误差平方求平均]

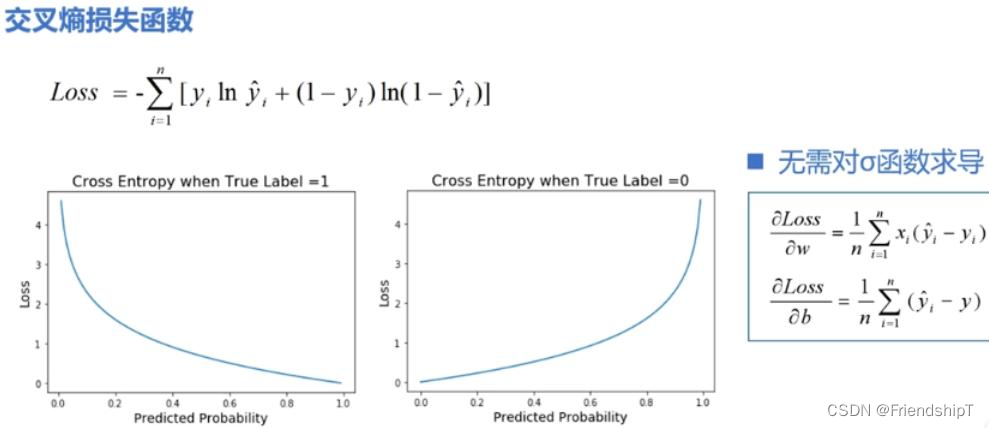
#### 2.2.2 交叉熵损失函数

交叉熵损失函数广泛应用于分类问题，特别是多分类和二分类问题。交叉熵衡量的是两个概率分布之间的差异，因此在输出层使用softmax激活函数时，交叉熵损失函数能够有效地指导模型学习概率分布。

# 示例：在Keras中使用交叉熵损失函数进行二分类

# 假设y_true是真实的标签，y_pred是模型预测的概率分布
# 使用binary_crossentropy作为损失函数
loss = keras.losses.binary_crossentropy(y_true, y_pred)

#### 2.2.3 对数似然损失

对数似然损失函数是交叉熵的一种等价表述，在统计学中广泛应用。它通过最大化似然函数来提升模型的性能，常用于广义线性模型和深度学习的分类任务。

### 2.3 损失函数的数学原理

#### 2.3.1 损失函数的优化过程

损失函数的优化过程是通过迭代更新模型参数来最小化损失函数值。这一过程涉及计算损失函数相对于模型参数的梯度，并利用这些梯度信息来调整参数。梯度下降算法及其变体（如Adam、RMSprop）是实现这一过程的常用方法。

#### 2.3.2 损失函数的梯度计算

梯度是损失函数关于参数的导数，它指导了损失函数沿着参数空间下降最快的方向。在实践中，梯度可以通过数值方法（如有限差分法）或解析方法（如反向传播算法）计算得出。计算梯度是优化算法的核心步骤，直接关系到模型性能的提升。

# 使用反向传播算法计算梯度的简化代码

# 初始化模型参数
weights = [w_init1, w_init2, ...]

# 定义损失函数
def loss_function(x, y, weights):
    # 损失函数的具体实现
    pass

# 计算损失函数关于参数的梯度
def compute_gradient(x, y, weights):
    # 计算梯度的具体实现，通常涉及链式法则
    pass

以上章节内容详细地探讨了损失函数在机器学习中的理论基础，并通过示例代码和逻辑分析，解释了如何在实践中应用这些理论。在下一章节，我们将深入探讨损失函数与不同机器学习任务的匹配，以及如何在具体场景中选择和应用损失函数。

# 3. 损失函数与不同机器学习任务的匹配

## 3.1 分类任务中的损失函数选择

### 3.1.1 二分类问题的损失函数

在二分类问题中，我们通常有两种结果：是或否，例如一封邮件是垃圾邮件或非垃圾邮件。在Keras中，常用的损失函数是二元交叉熵损失函数（binary cross-entropy），它是衡量模型输出的概率分布与实际标签概率分布之间的差异。在二分类问题中，我们假设模型输出的是正类的概率。

代码块示例：

from keras import backend as K
from keras.losses import binary_crossentropy

def binary_cross_entropy(y_true, y_pred):
    return K.mean(binary_crossentropy(y_true, y_pred), axis=-1)

# 逻辑分析：
# 1. 导入所需的函数。
# 2. 定义一个计算二元交叉熵的函数。
# 3. 使用binary_crossentropy计算单个样本的损失值。
# 4. 用K.mean计算整个批次的平均损失。

### 3.1.2 多分类问题的损失函数

在多分类问题中，类别的数量超过了两个。例如，一张图片可能是猫、狗或鸟。在这种情况下，通常使用分类交叉熵损失函数（categorical cross-entropy）。如果使用softmax激活函数作为输出层，Keras提供了categorical_crossentropy损失函数。

代码块示例：

from keras.losses import categorical_crossentropy

# 假设y_true是one-hot编码的标签，y_pred是模型的预测
loss_value = categorical_crossentropy(y_true, y_pred)

## 3.2 回归任务中的损失函数选择

### 3.2.1 线性回归的损失函数

在线性回归中，预测值通常与实际值之间的差异（残差）被最小化。最常用的损失函数是均方误差损失函数（Mean Squared Error, MSE），它通过取预测值和真实值之间差异的平方的平均值来进