【网络架构与损失函数】：在不同架构中选择与优化损失函数

# 1. 网络架构与损失函数的基本概念

## 1.1 网络架构简介
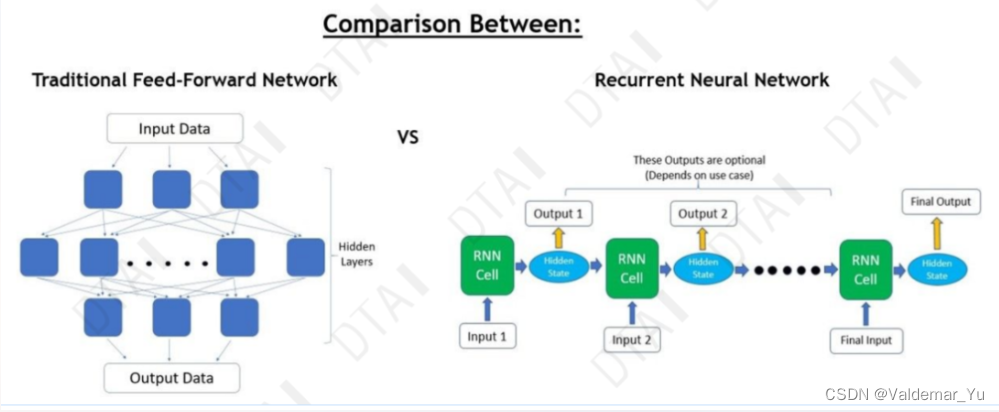
在网络架构中，基本的网络形式包括前馈神经网络、卷积神经网络和循环神经网络。这些架构拥有各自独特的结构与特点，决定了其在不同应用领域的表现。

## 1.2 损失函数的定义
损失函数，也称目标函数，衡量的是模型的预测值与实际值之间的差异。它是神经网络学习过程中的核心，用于引导网络通过不断迭代调整权重以最小化损失。

## 1.3 网络架构与损失函数的关系
网络架构决定了数据的流动方式，而损失函数则提供了优化的依据。正确选择损失函数对于模型的学习效率和最终性能至关重要，二者需要相互配合以达到最佳的训练效果。

# 2. 损失函数在不同网络架构中的角色

## 2.1 损失函数与前馈神经网络

### 2.1.1 前馈神经网络的工作原理

前馈神经网络是最基本的神经网络结构之一，其信息流动方式是单向的，从输入层开始，经过隐藏层处理后，直接流向输出层。在前馈神经网络中，每一层神经元的输出只会影响下一层神经元的输入。该网络通常用于解决分类和回归问题。

### 2.1.2 损失函数在前馈网络中的应用

在前馈神经网络中，损失函数用于度量模型输出与真实标签之间的差异。在训练过程中，通过反向传播算法和梯度下降法不断调整网络参数，以最小化损失函数的值。常用的损失函数包括均方误差（MSE）和交叉熵损失。

import numpy as np

# 定义均方误差函数
def mse_loss(y_true, y_pred):
    return np.mean((y_true - y_pred) ** 2)

# 定义交叉熵损失函数
def cross_entropy_loss(y_true, y_pred):
    return -np.mean(y_true * np.log(y_pred) + (1 - y_true) * np.log(1 - y_pred))

以上代码展示了两种基本损失函数的实现方式。均方误差直接计算预测值与真实值之间的平方差，而交叉熵损失是通过计算两个概率分布间的差异度量损失。在实际应用中，选择合适的损失函数对于模型性能有着重要影响。

## 2.2 损失函数与卷积神经网络

### 2.2.1 卷积神经网络的结构特点

卷积神经网络（CNN）是深度学习中用于处理图像和视频数据的一类神经网络。它能够通过卷积层自动提取数据的特征，而不需要人工设计特征。CNN主要由卷积层、池化层和全连接层组成，其中卷积层和池化层是其核心组件。

### 2.2.2 损失函数在卷积网络中的选择

在卷积神经网络中，损失函数的选用依赖于具体的任务类型。对于分类问题，交叉熵损失是最常用的损失函数之一。当涉及到图像分割等像素级预测时，通常使用像素级的损失函数，如均方误差或交叉熵损失，有时会结合注意力机制或条件随机场等技术。

# 示例：使用交叉熵损失的计算
def cross_entropy(y_true, y_pred):
    epsilon = 1e-15 # 防止数值不稳定
    y_pred = np.clip(y_pred, epsilon, 1 - epsilon)
    return -np.sum(y_true * np.log(y_pred))

在该段代码中，实现了一个简单的交叉熵损失函数。注意，为了避免数值不稳定问题，在计算对数之前对预测值进行了裁剪。

## 2.3 损失函数与循环神经网络

### 2.3.1 循环神经网络的序列处理机制

循环神经网络（RNN）特别适合处理序列数据，如时间序列数据、语音、文本等。其网络结构含有循环单元，允许信息在不同时间步之间传递和存储。RNN的这种机制让它能够捕捉到序列数据中的时间依赖性。

### 2.3.2 损失函数在循环网络中的应用

对于循环神经网络，损失函数的选择同样基于所面对的特定任务。对于序列分类问题，交叉熵损失通常是首选。而在序列生成任务中，如机器翻译或语音合成，可能会使用特定的损失函数，比如teacher forcing策略，该策略结合了交叉熵损失和目标序列的预测输出。

def sequence_cross_entropy(y_true, y_pred):
    losses = []
    for i in range(y_true.shape[1]):
        loss = cross_entropy(y_true[:, i, :], y_pred[:, i, :])
        losses.append(loss)
    return np.mean(losses)

在这段代码中，实现了一个适用于序列数据的交叉熵损失函数，它对序列中每个时间步的输出单独计算交叉熵损失，然后取平均值作为最终损失值。

通过本章的介绍，我们可以看到损失函数在不同网络架构中的角色和应用，其选择和使用直接影响了网络的学习效果和预测性能。下一章将深入探讨损失函数的理论基础与计算方法。

# 3. 损失函数的理论基础与计算方法

在探讨了损失函数在不同网络架构中的角色之后，接下来深入理解损失函数的理论基础和计算方法显得尤为重要。本章将详细阐述损失函数的目标分类、理论基础、以及它们的具体计算方法。

## 3.1 损失函数的基本理论

### 3.1.1 损失函数的目标和分类

损失函数，或称成本函数，是衡量模型预测值与真实值之间差异的函数。其主要目标是提供一个量化指标，用于引导模型参数的更新和优化。在机器学习和深度学习的训练过程中，损失函数通过计算损失值来反映模型性能的优劣，从而驱动优化算法调整模型参数以最小化损失。

损失函数的分类主要取决于具体的任务类型和模型形式。常见的分类包括：

- 回归任务：均方误差（MSE）、绝对误差（MAE）、Huber损失等。
- 分类任务：交叉熵损失（Cross-Entropy Loss），特别地，对于多分类问题有softmax交叉熵损失。
- 优化特定指标的任务：比如在目标检测中使用的是Smooth L1 Loss，其结合了MSE和MAE的特点。

### 3.1.2 不同类型损失函数的理论基础

理解不同类型损失函数的理论基础，对于选择合适的损失函数至关重要。

- 均方误差（MSE）：通过计算预测值与真实值差的平方和的均值，惩罚模型在大误差上的损失，适合于回归任务。
- 绝对误差（MAE）：计算预测值与真实值差的绝对值的平均，对异常值的惩罚相对较小，鲁棒性较好。
- 交叉熵损失（Cross-Entropy Loss）：衡量两个概率分布之间的差异。在分类任务中，它度量了预测的概率分布与实际标签的分布之间的差异，与模型预测的不确定性有关。

## 3.2 损失函数的计算方法

### 3.2.1 常见损失函数的数学表达式

以几种常见的损失函数为例：

- 均方误差（MSE）: $$L(y, \hat{y}) = \frac{1}{N} \sum_{i=1}^{N} (y_i - \hat{y}_i)^2$$
- 绝对误差（MAE）: $$L(y, \hat{y}) = \frac{1}{N} \sum_{i=1}^{N} |y_i - \hat{y}_i|$$
- 交叉熵损失（Cross-Entropy Loss）: $$L(y, \hat{y}) = -\frac{1}{N} \sum_{i=1}^{N} [y_i \log(\hat{y}_i) + (1 - y_i) \log(1 - \hat{y}_i)]$$

其中 $y_i$ 表示真实值，$\hat{y}_i$ 表示预测值，$N$ 是样本数量。

### 3.2.2 实际计算过程中的数值方法

在实际计算中，损失