【传统与深度学习对比】：损失函数在算法中的角色差异分析

# 1. 损失函数在机器学习中的基础概念

在机器学习的训练过程中，损失函数扮演了至关重要的角色。它是一种衡量模型预测值与真实值之间差异的数学函数，直接影响到模型的训练效果。损失函数的基本目标是提供一个量化的误差信号，用于指导模型的参数更新，使模型的预测更加准确。

## 1.1 损失函数的目的和作用

损失函数的目的是通过最小化损失来改进模型的性能。这个最小化的过程通常通过优化算法来实现，如梯度下降法。损失函数的类型不同，其优化方法和适用场景也有所区别。

## 1.2 常见的损失函数类型

在机器学习中，常见的损失函数包括均方误差（MSE）、交叉熵损失和绝对误差损失等。每种损失函数都有其特点和适用的场景。例如，均方误差通常适用于回归问题，而交叉熵损失则广泛应用于分类问题。

## 1.3 损失函数的选择

选择合适的损失函数对于模型的训练至关重要。通常，需要根据具体问题的性质来决定使用哪种损失函数。例如，在二分类问题中，交叉熵损失能够提供比均方误差更有效的梯度信息，因此更适合用于这类问题的训练。接下来的章节将会详细探讨如何根据不同问题选择合适的损失函数。

# 2. 传统机器学习中的损失函数

### 2.1 传统损失函数的类型与选择

#### 2.1.1 常见的损失函数介绍
在传统机器学习中，损失函数（Loss Function）是评价模型预测值与真实值差异的重要指标，是优化算法的依据。常见的传统损失函数主要包括以下几种：

1. **均方误差（MSE）**：回归问题中最为常用的损失函数之一，计算预测值与真实值差的平方的平均值。公式如下：
\[ MSE = \frac{1}{N} \sum_{i=1}^{N}(y_i - \hat{y_i})^2 \]
其中，\(y_i\) 和 \(\hat{y_i}\) 分别是真实值和预测值，N 是样本总数。

2. **绝对误差（MAE）**：计算预测值与真实值之间差的绝对值的平均值。公式为：

\[ MAE = \frac{1}{N} \sum_{i=1}^{N}|y_i - \hat{y_i}| \]

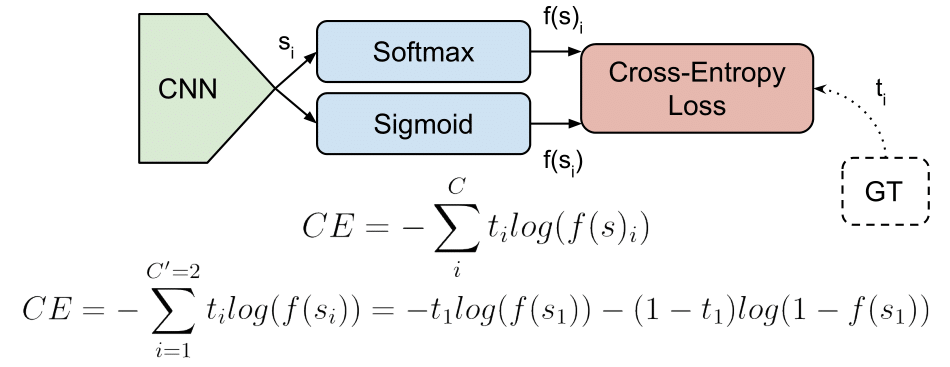
3. **交叉熵损失函数（Cross-Entropy Loss）**：常用于分类问题，度量模型预测的概率分布与真实概率分布之间的差异。对于多分类问题，交叉熵损失可以定义为：

\[ CE = -\sum_{c=1}^{M} y_c \log(p_c) \]
其中，\(M\) 是类别数，\(y_c\) 是一个指示器（0或1），如果样本的真实类别为c，则为1，\(p_c\) 是模型预测样本属于类别c的概率。

4. **零一损失（0-1 Loss）**：用于分类问题的损失函数，当预测类别与真实类别一致时损失为0，否则为1。由于其不可导性，通常不直接用于梯度下降法。

5. **Hinge Loss**：支持向量机（SVM）中常用的损失函数，适用于线性分类器，对分类错误的样本给予惩罚。

#### 2.1.2 如何针对不同问题选择合适的损失函数
针对不同问题选择合适的损失函数时，主要考虑以下几个方面：

1. **问题类型**：确定是回归问题还是分类问题。
- 回归问题：首选MSE或MAE。
- 分类问题：优先考虑交叉熵损失或Hinge Loss。

2. **数据特性**：了解数据的分布和特性。
- 对于异常值敏感的问题，可能会选择MAE而不是MSE。

3. **模型输出**：了解模型的输出是什么。
- 如果是概率分布，交叉熵损失是更佳选择。

4. **优化算法**：选择的损失函数是否能与优化算法兼容。
- 一些优化算法对损失函数的可微性有特定要求。

5. **模型的解释性**：某些损失函数比其他损失函数更易于解释。

通过这些考虑因素，可以有针对性地为不同问题选择最合适的损失函数。

### 2.2 传统损失函数的优化方法

#### 2.2.1 梯度下降法与损失函数的关系
梯度下降法是机器学习中最常用的一类优化算法，其基本思想是通过迭代的方式不断更新模型参数以最小化损失函数值。在每一步迭代中，根据损失函数关于参数的梯度（即导数），沿着减少损失函数的方向更新参数：

\[
\theta_{\text{new}} = \theta_{\text{old}} - \alpha \nabla_\theta L(\theta)
\]

其中，\(\theta\) 是模型参数，\(L(\theta)\) 是损失函数，\(\alpha\) 是学习率，\(\nabla_\theta L(\theta)\) 是损失函数关于参数的梯度。

梯度下降法包括批量梯度下降（Batch Gradient Descent）、随机梯度下降（Stochastic Gradient Descent）和小批量梯度下降（Mini-batch Gradient Descent）三种常见形式，其中随机梯度下降因其高效的计算速度在大数据时代特别受欢迎。

#### 2.2.2 正则化技术在损失函数中的应用
正则化是防止过拟合的有效手段，它通过在损失函数中加入一个额外的项（通常是L1或L2范数项）来惩罚模型的复杂度。常见的正则化技术包括：

1. **L1正则化（Lasso）**：加入L1范数项以鼓励模型参数稀疏化。

\[ L_{\text{L1}} = L + \lambda \sum_{j=1}^{p}|\theta_j| \]
其中，\(\lambda\) 是正则化系数，\(p\) 是参数数量。

2. **L2正则化（Ridge）**：加入L2范数项，使得参数值不会过大。

\[ L_{\text{L2}} = L + \lambda \sum_{j=1}^{p}\theta_j^2 \]

3. **Elastic Net**：同时使用L1和L2范数，结合Lasso和Ridge的优点。

通过将正则化项加入到损失函数中，可以控制模型复杂度，防止模型对训练数据过度拟合，从而提高模型的泛化能力。正则化系数\(\lambda\)的选择通常依赖于模型和数据集的特性，以及通过交叉验证进行调整。

### 2.3 传统方法中的过拟合与欠拟合问题

#### 2.3.1 过拟合与欠拟合的概念
在机器学习中，模型对训练数据的拟合程度是一个重要的考虑因素。如果一个模型过于复杂，并且对训练数据学习得太好，以至于它捕捉到了数据中的噪声和细节，而不能泛化到新的数据上，这种情况被称为**过拟合（Overfitting）**。相对地，如果模型过于简单，无法捕获数据的真实结构，导致其在训练数据和测试数据上的表现都不理想，这种情况被称为**欠拟合（Underfitting）**。

#### 2.3.2 损失函数在平衡过拟合与欠拟合中的作用
损失函数不仅用于衡量模型的性能，还影响着模型是否容易过拟合或欠拟合：

1. **减少过拟合**：
- 使用正则化项：L1或L2正则化可以限制模型参数的大小，避免模型复杂度过高。
- 简化模型：选择适当的模型结构，避免过复杂的模型。
- 增加数据量：过拟合很大程度上是因为训练数据不足，数据集越大，模型越难以对噪声过度拟合。

2. **避免欠拟合**：
- 选用更复杂的模型：如果模型过于简单，可能需要选用更高维的特征空间，或者采用更复杂的模型。
- 优化模型结构：可能需要调整神经网络的层数或支持向量机的核函数。

3. **调整学习率**：过高的学习率可能导致欠拟合，而过低的学习率可能导致过拟合。

4. **早停（Early Stopping）**：在训练过程中，如果验证集的损失不再下降，停止训练以防止过拟合。

通过上述方法，损失函数在模型的训练过程中起到了“调节器”的作用，帮助模型在复杂度和泛化能力之间取得平衡。

# 3. 深度学习中的损失函数

深度学习改变了我们处理复杂数据问题的方式，其性能的提升与损失函数息息相关。本章节将深入探讨深度学习中损失函数的特点，优化策略，以及在实际应用中可能出现的问题。

## 3.1 深度学习损失函数的特点

### 3.1.1 损失函数在深度网络中的角色

深度学习模型通常包含多层的非线性变换，这样的网络结构旨在学习数据的高级表示。损失函数在这一过程中承担了评估模型预测与真实值差异的角色，是模型训练的核心。

对于深度网络，损失函数的一个重要特性是能够反映出模型输出与真实标签之间的差异程度。这种差异通常以损失值的形式表达，损失值的大小直接关联到模型参数的更新方向和幅度。

### 3.1.2 深度学习特有的损失函数类型

深度学习领域引入了许多新的损失函数类型，以应对不同任务的需求。例如，交叉熵损失函数在分类问题中广泛应用，它能够有效地处理类别不平衡问题。而均方误差（MSE）损失函数则常用于回归任务。

在某些特定任务中，如序列生成或强化学习，还出现了基于策略梯度的损失函数，如策略梯度损失（Policy Gradient Loss），这些损失函数能够更好地反映问题的结构特征。

## 3.2 深度学习损失函数的优化策略

### 3.2.1 反向传播算法与损失函数的协同

反向传播算法（Backpropagation）是深度学习中最为核心的优化技术之一。它的作用是通过损失函数的梯度信息来更新模型参数，