【深度探索优化算法】：损失函数与梯度下降的黄金搭配

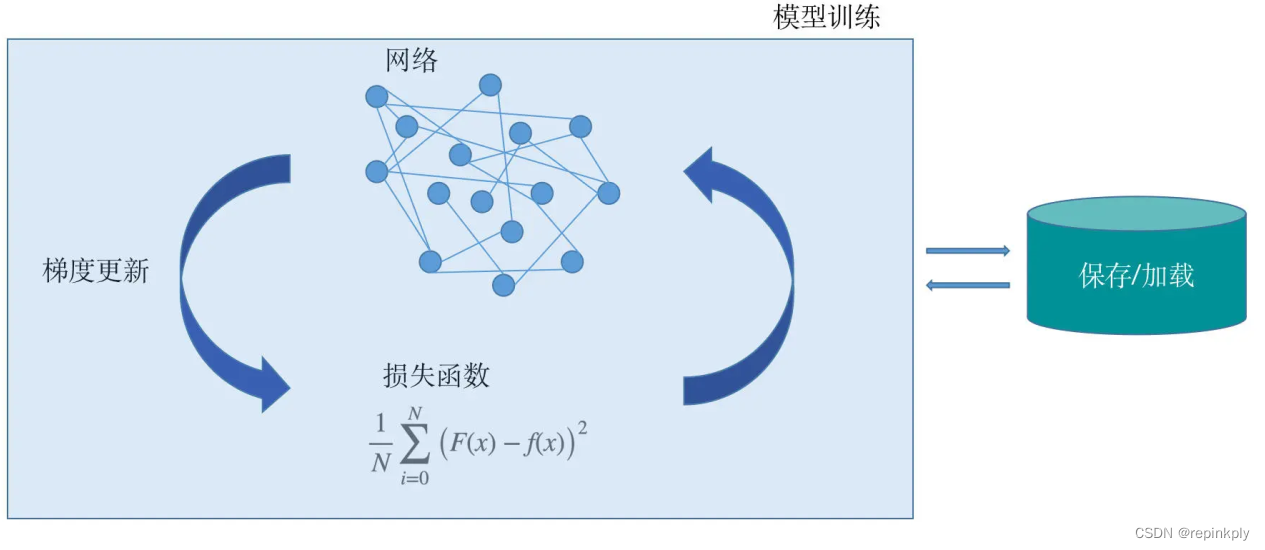
# 1. 优化算法基础与重要性

在机器学习和深度学习领域，优化算法扮演着至关重要的角色。它们是训练模型的核心，负责调整模型参数以最小化损失函数，进而提升模型的预测性能。优化算法的好坏直接影响到模型收敛的速度和质量，因此理解优化算法的基础知识和重要性，对于从事IT行业的专业人士来说，是提升模型性能和工作效率的关键。

## 1.1 优化问题的本质

优化问题在数学上是寻找一个或多个变量的值，使得一个目标函数达到最优（最大或最小）。在机器学习中，目标函数通常是损失函数，我们希望找到一组参数，使得损失函数的值尽可能小。这一过程在计算机科学中被称为搜索最小化（或最大化）问题。

## 1.2 优化算法的分类

根据不同的应用场景和条件，优化算法可以分为几类：
- **确定性算法**：如梯度下降、牛顿法等，每一步的搜索都根据确定性规则进行。
- **随机算法**：如随机梯度下降（SGD），在每一步中引入随机性，以应对大规模数据集或噪声数据。
- **启发式算法**：如模拟退火、遗传算法等，通常用于解决NP难问题，通过模拟自然界或其他启发式规则进行搜索。

了解并选择合适的优化算法对于解决实际问题是至关重要的。接下来的章节将详细探讨损失函数的类型与选择，以及具体的优化方法。

# 2. 损失函数的类型与选择

损失函数是机器学习中的核心概念，它衡量的是模型的预测值与真实值之间的差异。正确地选择和使用损失函数，对于训练出有效的模型至关重要。本章节将深入探讨损失函数的类型、理论基础以及在不同问题中的应用。

## 2.1 损失函数的理论基础

### 2.1.1 损失函数的定义与作用

损失函数，也称代价函数或目标函数，在数学上定义为模型预测值与实际值之间差异的度量。在训练过程中，损失函数的值越小，表示模型的预测越接近真实值，性能越好。它是优化算法寻找最优模型参数的“指南针”。

损失函数的作用不仅仅在于评价模型的性能，更重要的是，它为模型提供了一个学习的目标。通过最小化损失函数，模型参数可以不断地调整优化，从而使模型逐渐接近真实的映射关系。

### 2.1.2 常见损失函数的数学表达

在机器学习中，根据不同的问题类型，有多种损失函数可供选择。下面列举了一些常见的损失函数及其数学表达式：

- **均方误差（MSE）**，用于回归问题:
\[ MSE = \frac{1}{n} \sum_{i=1}^{n} (y_i - \hat{y}_i)^2 \]
其中，\(y_i\) 是真实值，\(\hat{y}_i\) 是预测值，\(n\) 是样本数量。

- **交叉熵损失（Cross-Entropy Loss）**，通常用于分类问题:
\[ CE = -\frac{1}{n} \sum_{i=1}^{n} [y_i \log(\hat{y}_i) + (1 - y_i) \log(1 - \hat{y}_i)] \]
这里，\(y_i\) 是一个表示类别的二进制向量，\(\hat{y}_i\) 是预测的概率分布。

- **绝对误差（Absolute Error）**:
\[ AE = \frac{1}{n} \sum_{i=1}^{n} |y_i - \hat{y}_i| \]

每种损失函数在不同的任务和数据分布下有不同的表现，选择合适的损失函数对模型性能至关重要。

## 2.2 损失函数在不同问题中的应用

### 2.2.1 分类问题中的损失函数

在分类问题中，交叉熵损失函数是较为常见的选择。这是因为交叉熵损失直接衡量了两个概率分布之间的差异，并且它具有很好的数学性质，如梯度稳定性和快速收敛等。

为了更好地处理不平衡的数据集，还衍生出了加权交叉熵损失等变种。在多标签分类问题中，可能会采用二元交叉熵损失或者Focal Loss来关注困难样本。

### 2.2.2 回归问题中的损失函数

对于回归问题，均方误差（MSE）是最直接的选择，它简单且容易理解。然而，当存在异常值时，MSE对异常值敏感，这可能导致梯度爆炸，从而影响模型的训练。为了提高模型的鲁棒性，可以使用平均绝对误差（MAE）或Huber损失函数。

### 2.2.3 其他复杂问题的损失函数

在一些复杂的问题中，可能会设计或选择特殊的损失函数来满足特定的需求。例如，在序列到序列的任务中，常用的损失函数包括序列损失（Sequence Loss）或者基于注意力机制的损失函数。

此外，在强化学习中，常用的损失函数是贝尔曼误差（Bellman Error），而在一些非监督学习问题中，可能会使用重构误差（Reconstruction Error）作为损失函数。

下面的表格总结了本章提及的损失函数及其特点：

| 损失函数 | 适用问题 | 优点 | 缺点 |
|-----------|----------|--------------------------------------|----------------------------|
| MSE | 回归 | 简单，易于计算 | 对异常值敏感 |
| 交叉熵 | 分类 | 良好的数学性质，快速收敛 | 可能对输出的分布有限制要求 |
| AE | 回归 | 对异常值较鲁棒 | 不如MSE光滑 |
| Huber | 回归 | 结合了MSE和MAE的优点，对异常值不敏感 | 计算稍复杂 |

在选择损失函数时，需要根据实际问题的需求和数据的特点进行细致的考量。在下一节中，我们将继续深入探讨梯度下降法的原理与实现，这是与损失函数紧密相关的优化算法。

# 3. 梯度下降法的原理与实现

## 3.1 梯度下降法的基本概念

### 3.1.1 梯度的概念及其几何意义

在数学和物理学中，梯度代表了一个标量场（如温度、电势等）相对于位置的改变率最大的方向。在优化算法中，梯度是损失函数相对于模型参数导数的集合，它指向了函数增长最快的方向。理解梯度的概念对于掌握梯度下降法至关重要。

在多维参数空间中，梯度的几何意义可以用向量场表示。每个点上的梯度向量指向函数增长最快的方向，其大小表示增长速率。直观来看，梯度的反方向就是函数下降最快的方向，这是梯度下降法名称的由来。

### 3.1.2 梯度下降的数学原理

梯度下降法是一种迭代优化算法，通过迭代更新模型参数来最小化损失函数。基本思想是沿损失函数的负梯度方向进行搜索，逐步逼近局部最小值点。

设定目标函数为\( f(\mathbf{w}) \)，其中 \(\mathbf{w}\) 是模型参数向量。参数更新规则如下：

\[
\mathbf{w}_{\text{new}} = \mathbf{w}_{\text{old}} - \eta \nabla f(\mathbf{w}_{\text{old}})
\]

其中，\( \eta \) 是学习率，控制着每一步参数更新的幅度；\( \nabla f(\mathbf{w}_{\text{old}}) \) 是在当前参数下的梯度值。学习率的选择至关重要，太小可能导致收敛速度过慢，而太大可能会导致收敛失败或参数更新过度。

## 3.2 梯度下降法的算法流程

### 3.2.1 参数更新规则

参数更新规则是梯度下降法的核心，直接影响到算法的性能。为了直观理解参数更新的过程，考虑一个简单的二次损失函数\( f(w) = w^2 \)，其梯度为\( \nabla f(w) = 2w \)。参数更新的过程可以用以下伪代码表示：

# 初始化参数w
w = 0
# 定义学习率
eta = 0.01
# 迭代次数
for i in range(100):
    # 计算梯度
    grad = 2 * w
    # 更新参数
    w = w - eta * grad

### 3.2.2 学习率的设置与调整

学习率是一个超参数，对算法的收敛速度和性能有很大影响。通常，学习率在训练开始时需要设置得较大以快速下降，然后随着训练的进行逐渐减小以稳定收敛。

一个常用的学习率调整策略是学习率衰减，例如：