【R语言债券分析速成课】：YieldCurve包打造个性化分析工具

# 1. R语言债券分析基础

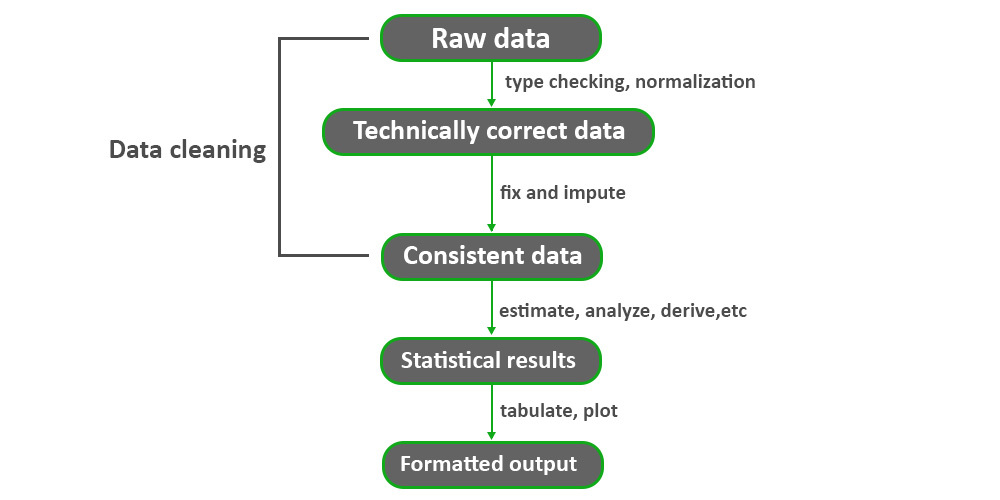
在这一章中，我们将介绍R语言在债券分析中的基础知识。债券分析作为一种金融分析的手段，通过使用R语言强大的统计和图形功能，可以帮助分析师更深入地理解债券市场及其复杂性。R语言作为一种广泛使用的开源统计软件，拥有大量的金融分析工具包，其中YieldCurve包是分析债券定价和市场利率关系的关键工具之一。

## 1.1 R语言在债券分析中的作用

R语言为债券分析提供了一个灵活的分析框架。它能够处理大量历史和实时数据，执行复杂的统计模型，生成丰富的图表来展示分析结果。特别是R的开源本质使其社区开发了许多针对特定金融问题的包，如YieldCurve，这些包极大地提高了债券分析的效率和深度。

## 1.2 债券分析中的关键指标

在深入使用YieldCurve包之前，了解债券市场的几个关键指标是必要的。这些指标包括收益率曲线、到期收益率（YTM）、票息利率、信用风险溢价等。这些指标是评估债券表现和市场情绪的关键，R语言可以帮助我们从数据中提取这些指标并进行深入分析。

## 1.3 准备进入YieldCurve包的世界

在本章的结尾，我们将介绍一些债券分析的基础知识，以及如何使用R语言作为分析工具。我们将为接下来的章节奠定基础，介绍YieldCurve包的安装和初步应用，以便读者能够在后续章节中更深入地探索债券市场和利率曲线。

这个开篇为接下来的章节内容搭建了稳固的基础，为读者在了解YieldCurve包及其在债券分析中的应用做好了准备。

# 2. 掌握YieldCurve包核心概念

### 2.1 YieldCurve包简介

#### 2.1.1 包的功能和应用场景
YieldCurve是R语言的一个重要包，主要用于构建和分析利率期限结构，是金融市场分析中的核心工具之一。该包的设计目标在于为金融专业人士、研究学者以及学生提供一个功能强大的环境，用以研究和理解利率的动态变化。

YieldCurve包提供了广泛的工具，用于计算和估计零息债券（spot rates）、即期收益率（forward rates）以及进行债券定价（bond pricing）。此外，它还支持复杂期限结构的可视化表示和敏感性分析。在实际应用中，YieldCurve包可以用于银行、资产管理公司、保险公司、对冲基金以及其他金融行业的用户分析债券市场和构建投资策略。

#### 2.1.2 安装与加载YieldCurve包
要开始使用YieldCurve包，首先需要在R环境中安装和加载它。这可以通过R语言的标准包管理函数来实现：

# 安装YieldCurve包
install.packages("YieldCurve")

# 加载YieldCurve包以供使用
library(YieldCurve)

执行上述命令后，YieldCurve包会被添加到R会话中，您可以开始使用包内提供的函数进行债券分析。安装过程一般只需执行一次，除非需要更新包到新版本。加载包则需要在每次新建R会话时重复执行。

### 2.2 利率期限结构理论

#### 2.2.1 利率期限结构的经济学意义
利率期限结构是描述不同到期日的债务工具（如国债）收益率如何随到期期限变化的关系。在金融市场中，利率期限结构是影响投资决策的关键因素之一。它揭示了市场对未来利率水平的预期，以及市场参与者对经济周期和政策变化的预测。

从经济学的角度来看，利率期限结构反映了多种因素的综合作用，包括流动性偏好、对未来通货膨胀的预期以及经济基本面因素。理解这一结构对于定价新发行的债券、评估现有债券的价值、进行资产配置、套期保值和风险管理都至关重要。

#### 2.2.2 常见的期限结构模型
在分析和预测利率期限结构时，研究者和市场参与者通常会使用几种常见的模型。以下是其中几个关键模型：

- **简单线性模型**：使用一阶多项式拟合利率与期限之间的关系，是最基础的模型之一。
- **Nelson-Siegel模型**：通过指数函数来模拟期限结构，它比线性模型有更强的灵活性和拟合能力。
- **CIR模型（Cox-Ingersoll-Ross模型）**：考虑了利率的均值回归特性和波动率，适用于模拟固定收益市场的动态变化。

这些模型在YieldCurve包中都有实现，用户可以根据自己的需要选择适用的模型进行分析。

### 2.3 利率期限结构估计方法

#### 2.3.1 参数估计方法
参数估计方法涉及对期限结构模型中的未知参数进行估计。这通常需要一组可观测的市场数据，如债券收益率数据。常用的参数估计方法包括：

- **最小二乘法（OLS）**：通过最小化误差的平方和找到最佳拟合线。
- **最大似然估计（MLE）**：寻找一组参数，使得观测数据出现的概率最大。

这些方法被广泛用于参数估计中，并在YieldCurve包中有相应的函数实现。

# 示例代码块 - 使用最大似然估计方法估计Nelson-Siegel模型参数
# 假设ns_model是一个已经设定好的Nelson-Siegel模型，data是一个包含债券收益率数据的数据框
ns_fit <- fit_model(ns_model, data, method = "MLE")

#### 2.3.2 非参数估计方法
非参数估计方法不假定期限结构的函数形式，而是直接从数据中提取信息。这种方法的优势在于模型的灵活性和对数据变化的敏感度。例如：

- **样条插值（Spline Interpolation）**：通过数据点创建平滑曲线，适合于构建光滑的利率期限结构。
- **核密度估计（Kernel Density Estimation）**：用于估计利率分布，尤其是在缺失观测数据的情况下。

非参数方法在YieldCurve包中的实现允许用户直接进行操作，而不需深入了解复杂的数学背景。

# 示例代码块 - 使用样条插值估计零息利率曲线
# 假定我们有时间期限和对应零息利率的数据点
zero_rates <- c(0.01, 0.015, 0.02, 0.025) # 示例零息利率数据
times_to_maturity <- c(1, 2, 3, 5) # 对应的期限数据

# 使用样条插值方法估计零息曲线
interpolated_zero_rates <- spline_zeros(zero_rates, times_to_maturity)

#### 2.3.3 模型选择和比较
面对多种可用的期限结构模型，选择合适的模型对分析结果至关重要。模型选择一般考虑模型的准确性、复杂度以及理论的适用性。模型比较可以通过统计检验（如AIC、BIC准则）以及预测准确度来实施。

# 示例代码块 - 比较不同模型的AIC值
# 假设ns_fit和cir_fit是使用不同方法拟合的模型
AIC(ns_fit)
AIC(cir_fit)

通过比较不同模型的AIC或BIC值，研究者可以决定使用哪一个模型进行进一步的分析。这样的模型选择和比较工作在实际分析中具有指导意义，并且需要对不同模型的假设和结果有深入的了解。

在下一章节中，我们将深入探讨如何使用YieldCurve包构建利率曲线，并在实践中运用这些理论和方法。

# 3. 利用YieldCurve包构建利率曲线

## 3.1 利率曲线的绘制基础

### 3.1.1 数据准备和输入

在金融市场分析中，绘制准确的利率曲线是评估债券投资和定价的关键。在使用YieldCurve包之前，我们需要准备好相应的时间序列数据。这些数据通常包括了不同到期期限的国债收益率数据。在R环境中，这些数据应该存储