布尔逻辑在哲学中的应用：形式逻辑和推理的基石，探索思维的本质

# 1. 布尔逻辑的基本原理**

布尔逻辑，又称二值逻辑，是一种数学逻辑系统，由乔治·布尔于19世纪中叶提出。它基于两个基本值：真（True）和假（False），并使用逻辑运算符（如与、或、非）来组合这些值。

布尔逻辑的运算符遵循特定的规则，称为布尔代数定律。这些定律定义了运算符之间的相互作用，并允许我们推导出复杂逻辑表达式的真值。布尔代数定律包括交换律、结合律、分配律和德·摩根定律。

# 2. 布尔逻辑在形式逻辑中的应用

布尔逻辑在形式逻辑中扮演着至关重要的角色，它为形式逻辑提供了严谨的数学基础，使得逻辑推理和证明具有明确的规则和标准。本章将探讨布尔逻辑在形式逻辑中的两个主要分支：命题逻辑和谓词逻辑。

### 2.1 命题逻辑

命题逻辑是布尔逻辑在形式逻辑中的基本应用，它处理的是命题之间的关系和推理。命题是一个真值确定的陈述，它可以取真或假两个值。

#### 2.1.1 命题的真值表

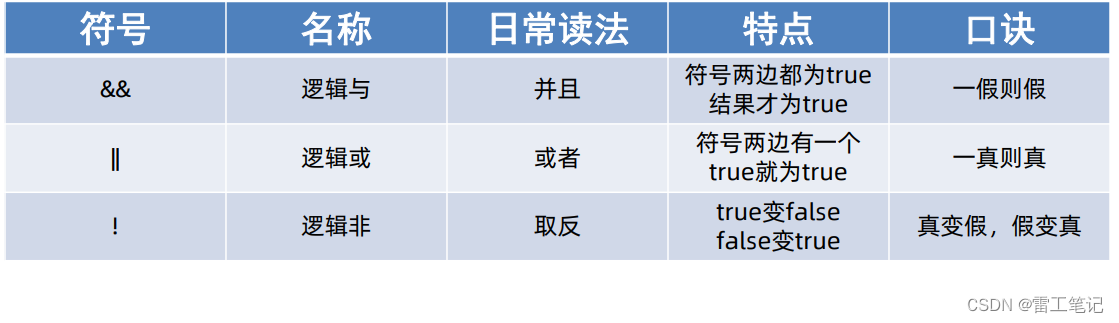
命题的真值表是描述命题之间关系的重要工具。真值表列出了所有可能的命题组合及其对应的真值。例如，对于两个命题 p 和 q，它们的真值表如下：

| p | q | p ∧ q | p ∨ q | p → q |
|---|---|---|---|---|
| 真 | 真 | 真 | 真 | 真 |
| 真 | 假 | 假 | 真 | 假 |
| 假 | 真 | 假 | 真 | 真 |
| 假 | 假 | 假 | 假 | 真 |

其中：

* p ∧ q 表示 p 和 q 同时为真
* p ∨ q 表示 p 或 q 至少有一个为真
* p → q 表示如果 p 为真，则 q 也为真

#### 2.1.2 命题演算规则

命题演算规则是一组用于推导新命题的规则。这些规则基于真值表，确保推导出的新命题与原命题具有相同的真值。常见的命题演算规则包括：

* **交换律：** p ∧ q = q ∧ p，p ∨ q = q ∨ p
* **结合律：** (p ∧ q) ∧ r = p ∧ (q ∧ r)，(p ∨ q) ∨ r = p ∨ (q ∨ r)
* **分配律：** p ∧ (q ∨ r) = (p ∧ q) ∨ (p ∧ r)，p ∨ (q ∧ r) = (p ∨ q) ∧ (p ∨ r)
* **吸收律：** p ∧ (p ∨ q) = p，p ∨ (p ∧ q) = p
* **双重否定律：** ¬¬p = p

### 2.2 谓词逻辑

谓词逻辑是对命题逻辑的扩展，它引入了谓词和量词的概念。谓词是一个描述对象或属性的陈述，而量词则表示对对象或属性的量化。

#### 2.2.1 谓词的量化

谓词的量化表示对对象或属性的普遍性或存在性。常见的量词包括：

* **全称量词：** ∀x (P(x)) 表示对于所有 x，P(x) 为真
* **存在量词：** ∃x (P(x)) 表示存在至少一个 x，使得 P(x) 为真

#### 2.2.2 谓词演算规则

谓词演算规则是用于推导新谓词的规则。这些规则基于量词和谓词之间的关系，确保推导出的新谓词与原谓词具有相同的真值。常见的谓词演算规则包括：

* **量词交换律：** ∀x ∃y (P(x, y)) = ∃y ∀x (P(x, y))
* **量词分配律：** ∀x (P(x) ∧ Q(x)) = (∀x P(x)) ∧ (∀x Q(x))
* **量词否定律：** ¬∀x P(x) = ∃x ¬P(x)，¬∃x P(x) = ∀x ¬P(x)
* **普遍例化律：** ∀x P(x) → P(a) (a 为任意常量)
* **存在实例化律：** ∃x P(x) → P(a) (a 为任意常量)

# 3.1 演绎推理

#### 3.1.1 三段论的有效性

三段论是一种演绎推理形式，由三个命题组成：大前提、小前提和结论。大前提和 p 小前提共同推出结论。三段论的有效性取决于其形式结构，与具体命题的内容无关。

**有效三段论的结构**

有效三段论的结构遵循以下规则：

- 大前提和 p 小前提中必须至少有一个全称命题。
-