布尔逻辑在区块链中的应用：确保分布式系统的安全和可靠性，构建可信的区块链

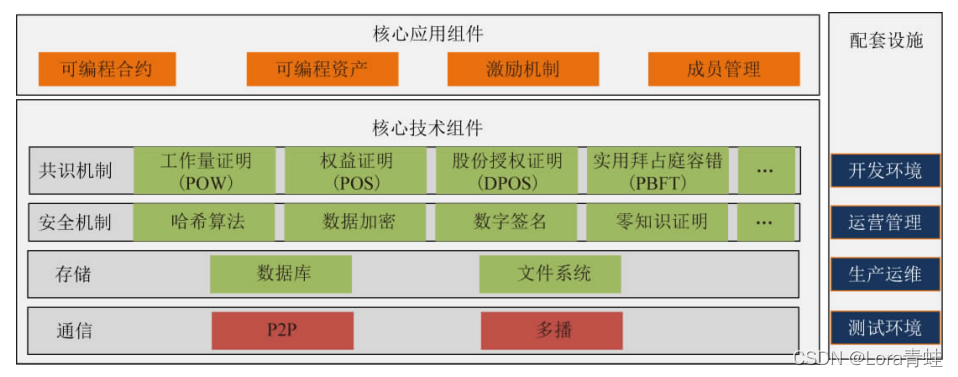
# 1. 区块链概述**

区块链是一种分布式、不可篡改的账本技术，用于记录交易和其他数据。它由一系列相互连接的块组成，每个块都包含一组交易记录。区块链由密码学保护，使其非常安全，并且由于其分布式性质，它具有高度的容错性。

区块链技术具有许多潜在应用，包括：

* **金融服务：**区块链可用于简化和保护金融交易，例如支付、清算和结算。
* **供应链管理：**区块链可用于跟踪和管理供应链中的商品，提高透明度和效率。
* **医疗保健：**区块链可用于保护医疗记录并改善患者护理。
* **政府服务：**区块链可用于提高政府服务的效率和透明度，例如投票和身份验证。

# 2. 布尔逻辑在区块链中的理论基础

布尔逻辑是区块链技术的理论基础之一，它提供了一套形式化的规则和符号，用于表示和操作逻辑命题。在区块链中，布尔逻辑被广泛应用于密码学、共识机制、智能合约和安全机制等多个方面。

### 2.1 布尔代数的基本概念

布尔代数是一种二元代数系统，它由以下元素组成：

- **布尔值：**真（True）和假（False）
- **布尔运算符：**与（AND）、或（OR）、非（NOT）
- **布尔变量：**表示命题或条件的符号

布尔代数的基本定律包括：

- **结合律：** (A AND B) AND C = A AND (B AND C)
- **交换律：** A AND B = B AND A
- **分配律：** A AND (B OR C) = (A AND B) OR (A AND C)
- **吸收律：** A AND (A OR B) = A
- **德摩根定律：** NOT (A AND B) = NOT A OR NOT B

### 2.2 布尔逻辑在密码学中的应用

布尔逻辑在密码学中扮演着至关重要的角色，它被用于设计和分析密码算法。例如：

- **哈希函数：**哈希函数是一种单向函数，它将任意长度的数据转换为固定长度的哈希值。布尔逻辑被用于设计哈希算法，以确保哈希值的唯一性和不可逆性。
- **数字签名：**数字签名是一种加密技术，用于验证消息的真实性和完整性。布尔逻辑被用于设计数字签名算法，以确保签名只能由私钥持有者生成，并且可以被公钥验证。
- **对称加密：**对称加密算法使用相同的密钥进行加密和解密。布尔逻辑被用于设计对称加密算法，以确保数据的机密性。

**代码块 1：**

def hash_function(data):
    """
    哈希函数示例
    :param data: 要哈希的数据
    :return: 哈希值
    """
    # 使用 SHA-256 算法生成哈希值
    hash_value = hashlib.sha256(data.encode()).hexdigest()
    return hash_value

**逻辑分析：**

代码块 1 展示了一个哈希函数的示例，它使用 SHA-256 算法将数据转换为哈希值。哈希函数的输入是一个字符串，输出是一个 64 位的十六进制字符串。

**参数说明：**

- `data`：要哈希的数据
- `hash_value`：哈希值

# 3. 布尔逻辑在区块链中的实践应用

### 3.1 区块链共识机制中的布尔逻辑

#### 3.1.1 工作量证明

工作量证明（PoW）是一种共识机制，要求矿工解决复杂的数学难题以验证区块。在 PoW 中，布尔逻辑用于定义难题的难度。

**代码块：**

def calculate_difficulty(block_height):
    """计算区块难度的函数。

    Args:
        block_height: 当前区块的高度。

    Returns:
        区块的难度。
    """

    # 根据区块高度调整难度。
    difficulty = 2 ** (block_height // 2016)

    # 确保难度不低于最低难度。
    difficulty = max(difficulty, 1)

    return difficulty

**逻辑分