排序算法的性能优化：从算法选择到代码实现

# 1. 排序算法概览**

排序算法是计算机科学中用于将数据元素按特定顺序排列的一类算法。它们广泛应用于各种领域，从数据分析到计算机图形学。排序算法的效率和性能对应用程序的性能至关重要。

排序算法的基本原理是将输入数据元素与一个或多个键值进行比较，并根据比较结果将元素重新排列。键值可以是数字、字符串或任何其他可比较的数据类型。排序算法根据其比较和重新排列数据的策略而有所不同。

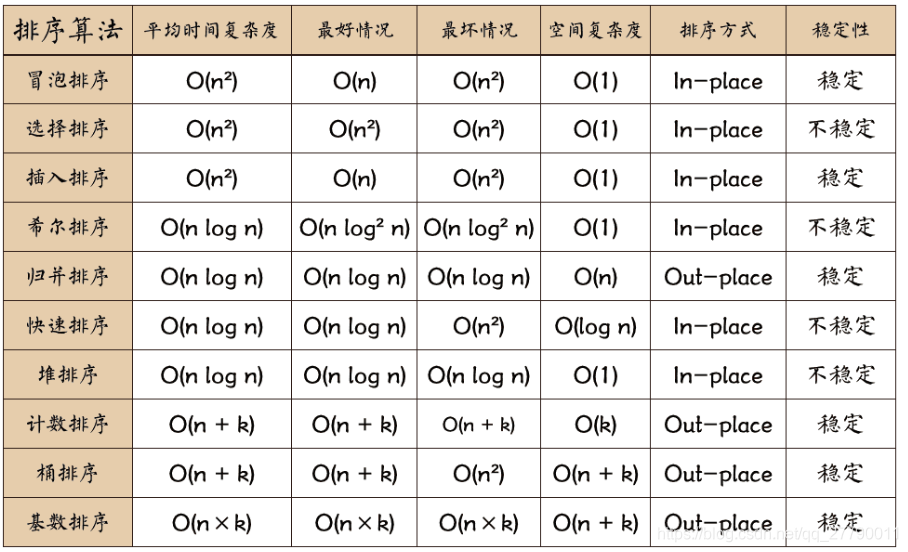
常见的排序算法包括冒泡排序、选择排序、插入排序、快速排序、归并排序和堆排序。每种算法都有其独特的优点和缺点，在不同的情况下表现不同。选择合适的排序算法对于优化应用程序的性能至关重要。

# 2. 排序算法的理论分析

### 2.1 时间复杂度和空间复杂度

#### 2.1.1 常见排序算法的时间复杂度

排序算法的时间复杂度是指执行排序操作所需的时间。常见排序算法的时间复杂度如下表所示：

| 排序算法 | 最好情况 | 最坏情况 | 平均情况 |
|---|---|---|---|
| 冒泡排序 | O(n) | O(n^2) | O(n^2) |
| 选择排序 | O(n^2) | O(n^2) | O(n^2) |
| 插入排序 | O(n) | O(n^2) | O(n^2) |
| 快速排序 | O(n log n) | O(n^2) | O(n log n) |
| 归并排序 | O(n log n) | O(n log n) | O(n log n) |
| 堆排序 | O(n log n) | O(n log n) | O(n log n) |

**代码块：**

def bubble_sort(arr):
    for i in range(len(arr) - 1):
        for j in range(len(arr) - 1 - i):
            if arr[j] > arr[j + 1]:
                arr[j], arr[j + 1] = arr[j + 1], arr[j]

**逻辑分析：**

冒泡排序算法的时间复杂度为 O(n^2)，因为算法需要遍历数组 n 次，每次遍历都需要比较 n 个元素。

#### 2.1.2 常见排序算法的空间复杂度

排序算法的空间复杂度是指执行排序操作所需的空间。常见排序算法的空间复杂度如下表所示：

| 排序算法 | 空间复杂度 |
|---|---|
| 冒泡排序 | O(1) |
| 选择排序 | O(1) |
| 插入排序 | O(1) |
| 快速排序 | O(log n) |
| 归并排序 | O(n) |
| 堆排序 | O(1) |

**代码块：**

def merge_sort(arr):
    if len(arr) <= 1:
        return arr

    mid = len(arr) // 2
    left_half = merge_sort(arr[:mid])
    right_half = merge_sort(arr[mid:])

    return merge(left_half, right_half)

def merge(left, right):
    merged = []
    left_index = 0
    right_index = 0

    while left_index < len(left) and right_index < len(right):
        if left[left_index] <= right[right_index]:
            merged.append(left[left_index])
            left_index += 1
        else:
            merged.append(right[right_index])
            right_index += 1

    merged.extend(left[left_index:])
    merged.extend(right[right_index:])

    return merged

**逻辑分析：**

归并排序算法的空间复杂度为 O(n)，因为算法需要创建一个与原始数组大小相同的临时数组来存储合并后的结果。

### 2.2 稳定性、原地排序和外部排序

#### 稳定性

稳定性是指当两个元素具有相同的排序键时，排序算法是否保持它们在输入中的相对顺序。稳定排序算法会保持相对顺序，而非稳定排序算法则不会。

**代码块：**

def stable_sort(arr):
    for i in range(len(arr) - 1):
        for j in range(len(arr) - 1 - i):
            if arr[j] > arr[j + 1]:
                arr[j], arr[j + 1] = arr[j + 1], arr[j]
            elif arr[j] == arr[j + 1]:
                # 保持相对顺序
                pass

**逻辑分析：**

这个排序算法是稳定的，因为当两个元素相等时，它会保持它们的相对顺序。

#### 原地排序

原地排序是指排序算法不需要额外的空间来执行排序操作。

**代码块：**

def in_place_sort(arr):
    for i in range(len(arr) - 1):
        min_index = i
        for j in range(i + 1, len(arr)):
            if arr[j] < arr[min_index]:
                min_index = j
        arr[i], arr[min_index] = arr[min_index], arr[i]