并行排序算法：多核时代的高效排序技术

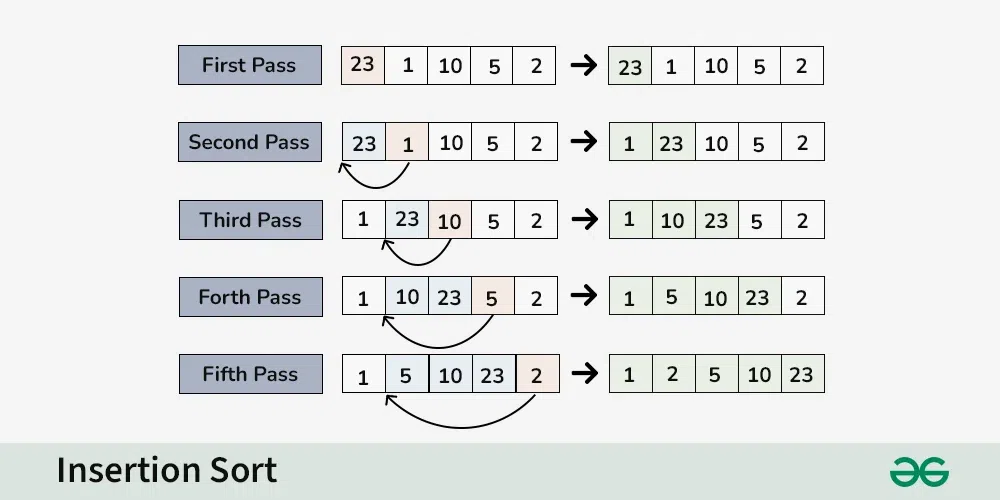
# 1. 并行排序算法概述

并行排序算法是一种利用多核处理器或分布式计算环境来加速排序过程的算法。它通过将排序任务分解成多个子任务，并行执行这些子任务，从而显著提高排序效率。

并行排序算法的优势在于它可以充分利用现代计算机的并行计算能力，在处理海量数据时表现出优异的性能。随着数据规模的不断增长，并行排序算法在各种应用领域中变得越来越重要，例如大数据分析、科学计算和机器学习。

# 2. 并行排序算法理论基础

### 2.1 并行计算模型

并行计算模型描述了并行算法如何分配和协调计算任务。主要有两种并行计算模型：

#### 2.1.1 共享内存模型

在共享内存模型中，所有处理器共享一个全局内存空间。处理器可以并行访问和修改内存中的数据，从而实现数据共享和同步。共享内存模型适用于小规模并行系统，如多核处理器或多处理器系统。

#### 2.1.2 分布式内存模型

在分布式内存模型中，每个处理器都有自己的私有内存空间。处理器之间通过消息传递机制进行通信和数据交换。分布式内存模型适用于大规模并行系统，如集群或云计算平台。

### 2.2 并行排序算法分类

并行排序算法可分为两大类：

#### 2.2.1 分而治之算法

分而治之算法将排序问题分解成较小的子问题，并行解决子问题，再将子问题的解合并得到最终结果。典型的分而治之算法包括快速排序和归并排序。

#### 2.2.2 归并排序算法

归并排序算法采用分治策略，将待排序序列递归地分成两半，并行对两半进行排序，然后将排序后的两半合并得到最终结果。归并排序算法的时间复杂度为 O(n log n)，空间复杂度为 O(n)。

### 2.3 并行排序算法的性能分析

并行排序算法的性能主要受时间复杂度和空间复杂度影响：

#### 2.3.1 时间复杂度

时间复杂度衡量算法执行所需的时间。并行排序算法的时间复杂度通常与算法并行度和通信开销有关。

#### 2.3.2 空间复杂度

空间复杂度衡量算法执行所需的空间。并行排序算法的空间复杂度通常与算法并行度和数据结构有关。

**代码块：**

def parallel_merge_sort(arr):
    if len(arr) <= 1:
        return arr

    mid = len(arr) // 2
    left_half = parallel_merge_sort(arr[:mid])
    right_half = parallel_merge_sort(arr[mid:])

    return merge(left_half, right_half)

def merge(left, right):
    i, j, merged = 0, 0, []
    while i < len(left) and j < len(right):
        if left[i] <= right[j]:
            merged.append(left[i])
            i += 1
        else:
            merged.append(right[j])
            j += 1

    while i < len(left):
        merged.append(left[i])
        i += 1

    while j < len(right):
        merged.append(right[j])
        j += 1

    return merged

**逻辑分析：**

该代码实现了并行归并排序算法。首先，它将待排序序列分解成两半，然后并行对两半进行排序。最后，它将排序后的两半合并得到最终结果。

**参数说明：**

* `arr`：待排序序列。

**时间复杂度：** O(n log n)

**空间复杂度：** O(n)

**表格：**

| 并行排序算法 | 时间复杂度 | 空间复杂度 | 并行度 |
|---|---|---|---|
| 快速排序 | O(n log n) | O(log n) | 高 |
| 归并排序 | O(n log n) | O(n) | 中等