排序算法的算法分析：从时间复杂度到空间复杂度

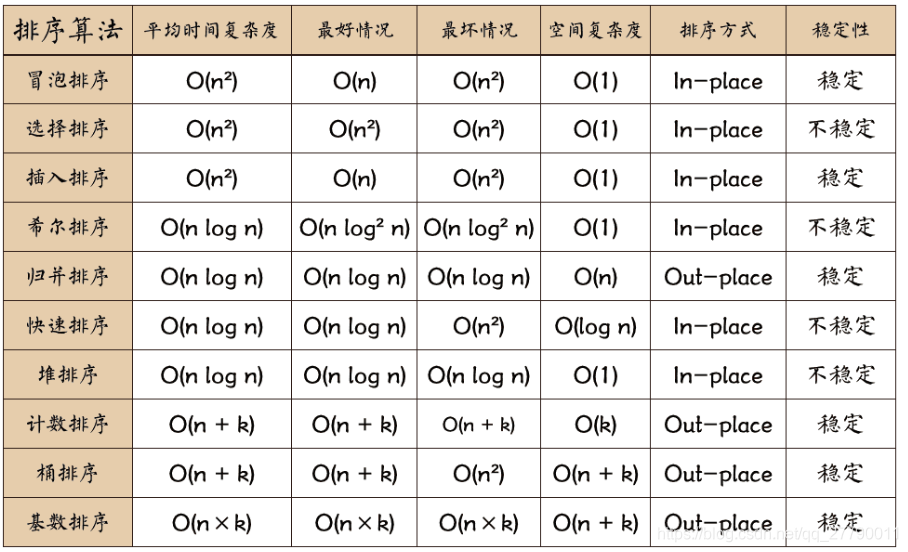
# 1. 排序算法概述

排序算法是计算机科学中用于对数据集合进行排序的基本算法。排序算法的目标是将数据集合中的元素按照某种顺序排列，例如升序或降序。排序算法在各种应用中至关重要，例如数据分析、数据库管理和搜索引擎。

排序算法有多种类型，每种算法都有其独特的优点和缺点。选择合适的排序算法取决于数据集合的规模、数据类型和所需的排序顺序。在本章中，我们将介绍排序算法的基本概念、分类和时间复杂度分析。

# 2. 排序算法的时间复杂度分析

时间复杂度是衡量算法效率的重要指标，它表示算法在不同输入规模下的执行时间。对于排序算法，时间复杂度主要取决于输入数组的长度 n。

### 2.1 冒泡排序

冒泡排序是一种简单易懂的排序算法，其基本思想是将相邻元素进行比较，并交换较大的元素到后面，依次遍历整个数组，直到所有元素按从小到大排列。

#### 2.1.1 最好情况时间复杂度

在最好情况下，当数组已经有序时，冒泡排序只需要遍历一遍数组，即可完成排序。此时，时间复杂度为 **O(n)**。

#### 2.1.2 最坏情况时间复杂度

在最坏情况下，当数组完全逆序时，冒泡排序需要遍历数组 n 次，每次遍历都需要进行 n 次比较和交换。此时，时间复杂度为 **O(n^2)**。

#### 2.1.3 平均情况时间复杂度

在平均情况下，冒泡排序的时间复杂度为 **O(n^2)**。这可以通过数学分析和实验验证得到。

### 2.2 选择排序

选择排序是一种不稳定的排序算法，其基本思想是每次从未排序的数组中找到最小（或最大）元素，并将其与未排序数组的第一个元素交换，依次遍历整个数组，直到所有元素按从小到大排列。

#### 2.2.1 最好情况时间复杂度

在最好情况下，当数组已经有序时，选择排序只需要遍历一遍数组，即可完成排序。此时，时间复杂度为 **O(n)**。

#### 2.2.2 最坏情况时间复杂度

在最坏情况下，当数组完全逆序时，选择排序需要遍历数组 n 次，每次遍历都需要进行 n 次比较和交换。此时，时间复杂度为 **O(n^2)**。

#### 2.2.3 平均情况时间复杂度

在平均情况下，选择排序的时间复杂度为 **O(n^2)**。这可以通过数学分析和实验验证得到。

### 2.3 插入排序

插入排序是一种稳定的排序算法，其基本思想是将未排序数组中的元素依次插入到已排序的数组中，保证已排序数组始终有序。

#### 2.3.1 最好情况时间复杂度

在最好情况下，当数组已经有序时，插入排序只需要遍历一遍数组，即可完成排序。此时，时间复杂度为 **O(n)**。

#### 2.3.2 最坏情况时间复杂度

在最坏情况下，当数组完全逆序时，插入排序需要遍历数组 n 次，每次遍历都需要进行 n 次比较和插入操作。此时，时间复杂度为 **O(n^2)**。

#### 2.3.3 平均情况时间复杂度

在平均情况下，插入排序的时间复杂度为 **O(n^2)**。这可以通过数学分