【自适应控制】：如何使倒立摆适应不断变化的环境


# 摘要
本文旨在为读者提供对自适应控制技术及其在倒立摆系统中应用的全面概述。首先，介绍了倒立摆系统的数学模型和基本控制策略，强调了动态平衡和系统状态表示的重要性。随后，详细阐述了自适应控制理论，包括其定义、类型、原理以及在设计自适应律和参数估计方法中的数学模型。文章还探讨了自适应控制器在倒立摆系统中的设计和仿真结果，以及实际应用中遇到的挑战和优化策略。最后，展望了自适应控制技术的未来发展趋势，特别是智能算法的融合以及在工业和教育领域的应用前景。

# 关键字
自适应控制；倒立摆系统；数学模型；控制器设计；仿真实验；算法优化

参考资源链接：[双闭环PID控制的一阶倒立摆系统设计与仿真验证](https://wenku.csdn.net/doc/3x2y907e5h?spm=1055.2635.3001.10343)
# 1. 自适应控制概述

自适应控制技术作为一种高级控制策略，其核心在于控制系统能够根据外部环境和内部状态的变化自动调整控制参数，以实现最佳的控制性能。这一技术的出现，有效地解决了复杂动态系统在面对不确定性和变化时的传统控制难题。

在探索自适应控制的过程中，我们首先需要了解其概念、特点以及在实际应用中的表现。它与传统控制方法的主要区别在于自我调整的能力，这种能力使得自适应控制器可以在没有人为干预的情况下，自行应对系统的不确定性和动态变化。

本章内容将作为后续章节深入探讨自适应控制在倒立摆系统中应用的理论基础和实践指导。接下来，我们将逐步揭开自适应控制的神秘面纱，从理论到实践，逐步深入解析这一前沿技术。

# 2. 倒立摆系统基础

### 2.1 倒立摆的数学模型

#### 2.1.1 动力学方程

倒立摆系统是控制理论中的经典实验模型，它的动态行为可通过牛顿第二定律建立数学模型。在最基本的假设下，我们可以认为倒立摆是一维的，即只在竖直平面内做往复摆动。对于一个典型的倒立摆系统，其动力学方程可由以下二阶非线性微分方程表示：

\[ m\ddot{x} + b\dot{x} + mg\sin(\theta) - u = 0 \]

其中，\( m \) 代表摆锤的质量，\( b \) 是阻尼系数，\( g \) 是重力加速度，\( \theta \) 是摆锤与垂直向上的角度，\( x \) 是摆锤底部在水平方向上的位移，\( u \) 表示施加在摆锤底部的控制力。

此处，为了简化模型，我们假设摆锤与地面之间的接触是理想的，不存在摩擦力。当摆锤垂直向上时，即 \( \theta = 0 \)，摆锤处于不稳定平衡状态，这也是倒立摆控制系统需要维持的动态平衡点。

#### 2.1.2 系统状态的表示

为了使用状态空间表示法对倒立摆进行控制，我们需要将上述二阶微分方程转化为一组一阶微分方程。定义状态变量 \( \textbf{x} \) 和控制输入 \( u \) 如下：

\[ \textbf{x} = \begin{bmatrix} x & \dot{x} & \theta & \dot{\theta} \end{bmatrix}^T \]

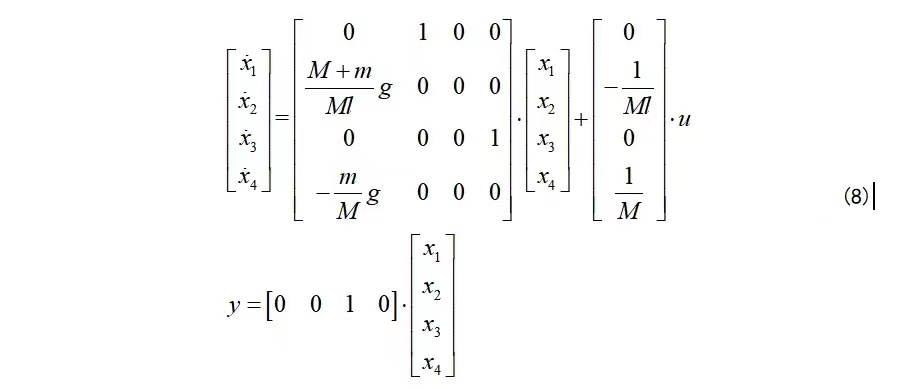
其中，\( x \) 和 \( \dot{x} \) 分别代表摆锤底部的水平位置和速度，\( \theta \) 和 \( \dot{\theta} \) 分别代表摆锤的角度和角速度。通过引入新的变量，我们可以将动力学方程转化为状态空间形式：

\[ \dot{\textbf{x}} = \begin{bmatrix} \dot{x} \\ \ddot{x} \\ \dot{\theta} \\ \ddot{\theta} \end{bmatrix} = \begin{bmatrix} x_2 \\ \frac{1}{m}[-bx_2 - mg\sin(x_3) + u] \\ x_4 \\ \frac{1}{I}[-b x_4 - mgl \sin(x_3) \cos(x_3)] \end{bmatrix} \]

其中，\( I \) 是摆锤相对于旋转轴的转动惯量，\( l \) 是摆锤质心到旋转轴的距离。通过上述转换，倒立摆的控制问题现在可表示为状态空间模型的线性或非线性控制问题。

### 2.2 倒立摆的控制策略

#### 2.2.1 传统控制方法

传统控制方法包括比例-积分-微分（PID）控制、线性二次调节器（LQR）等。PID 控制器通过调整比例、积分、微分三个参数来实现对系统的稳定控制。对于倒立摆系统，可以设计一个PID控制器来维持摆锤在平衡位置。

PID 控制器的输出 \( u(t) \) 可以表示为：

\[ u(t) = K_p e(t) + K_i \int_0^t e(\tau) d\tau + K_d \frac{de(t)}{dt} \]

其中，\( e(t) \) 是误差信号，\( K_p \)、\( K_i \) 和 \( K_d \) 分别是比例、积分、微分的增益。这些增益需要通过试验或优化算法进行调整以获得最佳性能。

#### 2.2.2 控制器的设计原则

设计倒立摆的控制器时，需要考虑系统的稳定性和响应特性。控制器的设计原则包括：

1. **稳定性**：控制器需要确保系统的稳定性，即在受到外部扰动时系统能够回到平衡状态。
2. **快速性**：系统需要有较快的响应速度，能够迅速对输入的变化做出反应。
3. **鲁棒性**：设计的控制器应具备一定的鲁棒性，即在参数变化和外部扰动下仍能保持良好的性能。
4. **实用性**：控制器设计应考虑工程实际，避免过于复杂的实现。

通过这些原则的指导下，我们可以设计出符合倒立摆系统要求的控制器，使其在各种情况下都能有效地进行稳定控制。接下来的章节中，我们将详细讨论自适应控制理论和在倒立摆中的应用，进一步深化对倒立摆控制系统设计的理解。

# 3. 自适应控制理论

自适应控制理论是现代控制理论的一个重要分支，它允许控制器在运行过程中根据系统的性能表现动态地调整其参数或结构。本章节将深入探讨自适应控制的基本概念、数学模型，以及它们在控制策略中的应用。

## 3.1 自适应控制的基本概念

### 3.1.1 自适应控制的定义

自适应控制是一种智能控制方法，它能够在没有精确模型或者模型发生变化的情况下，通过在线辨识系统参数或者状态，实现对系统的有效控制。与传统的固定参数控制方法不同，自适应控制器可以适应系统本身或者外部环境的变化，保持良好的控制性能。自适应控制的一个核心优势在于其具备的鲁棒性，即能在不确定性条件下工作。

### 3.1.2 自适应控制的类型和原理

自适应控制系统主要有两种类型：模型参考自适应控制（MRAC）和自校正控制（STC）。模型参考自适应控制通过调节控制参数使实际的系统输出跟随参考模型的输出，而自校正控制则是通过在线辨识系统模型并相应地调整控制器参数。自适应控制的原理基于对控制系统的实时监测和性能评估，通过一系列算法实现系统参数的在线估计和调整。

## 3.2 自适应控制的数学模型

### 3.2.1 参数估计方法

参数估计是自适应控制的核心环节之一，涉及到系统参数的实时估计。常用的参数估计方法包括最小二乘法、递归最小二乘法、卡尔曼滤波等。这些方法能够通过处理输入输出数据来辨识系统参数，为控制器调整提供依据。参数估计的过程中，需要考虑计算效率和准确性，以及噪声和干扰的影响。

### 3.2.2 自适应律的设计

自适应律是自适应控制器中的关键部分，它决定了控制参数如何根据参数估计的结果