【实战汇编编程】：多位十进制加法边界条件的处理之道


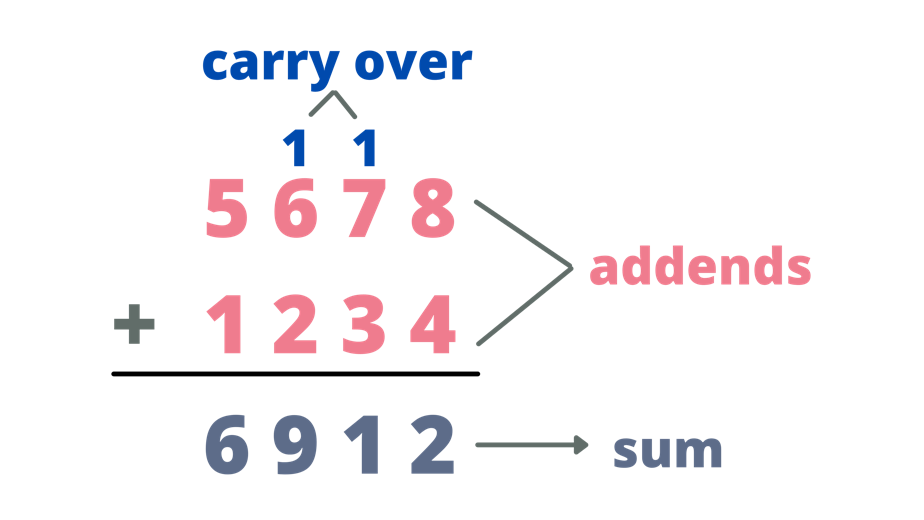
# 摘要
本文系统地探讨了汇编语言环境下多位十进制加法的实现及其边界条件的处理。首先介绍了汇编语言的基础知识和多位十进制数的表示方法，接着详细分析了边界条件的定义、分类以及在加法操作中的具体表现和处理方法。文章进一步通过编写汇编程序进行实践操作，并通过案例分析展示了多位十进制加法在财务软件和嵌入式系统中的应用。通过本研究，我们能够更好地理解并掌握汇编语言中处理多位十进制数加法的关键技术，并提出有效的边界条件处理策略，为相关领域的软件开发和系统优化提供了理论基础和实践经验。

# 关键字
汇编语言；边界条件；多位十进制加法；进位机制；错误处理；程序优化

参考资源链接：[8086汇编语言：实现多个十进制数相加](https://wenku.csdn.net/doc/1n6sveeu7m?spm=1055.2635.3001.10343)
# 1. 汇编语言与边界条件概述

## 1.1 汇编语言简介
汇编语言是一种低级编程语言，它与机器语言极其接近，但使用了人类可读的符号和词汇来表示机器代码指令。它是计算机硬件级别的编程语言，因此程序员可以通过汇编语言精确地控制硬件行为。

## 1.2 边界条件定义
边界条件指的是在输入或输出集合中，特定极端或极限值的情况。在软件开发中，正确处理边界条件是避免程序错误和安全漏洞的关键。

## 1.3 汇编语言与边界条件的联系
在汇编语言编程中，由于其直接与硬件交互的特性，边界条件处理尤为重要。正确处理好边界条件可以确保程序稳定运行，避免数据损坏和系统崩溃等问题。因此，本章将初步探讨汇编语言与边界条件的交互，为后续章节中多位十进制加法的实现和优化打下坚实的基础。

# 2. 汇编语言基础与多位十进制加法理论

### 2.1 汇编语言基础知识

汇编语言是与计算机硬件结构紧密相关的低级编程语言，它提供了对硬件操作的直接控制能力。汇编语言的特点包括对硬件操作的高度透明性、执行速度快和占用空间小。然而，这也导致了它的复杂性和编程难度较高。

#### 2.1.1 汇编语言的特点与分类

汇编语言主要有以下特点：
- **接近硬件**：汇编语言与机器语言仅有一步之遥，这让汇编程序员可以直接操作硬件资源。
- **依赖特定处理器架构**：不同的处理器架构（比如x86、ARM等）使用不同的指令集，因此汇编语言程序通常不具有跨平台性。
- **高度优化**：由于程序员能够精细控制每一步操作，因此可以针对特定的任务编写出高度优化的代码。

根据不同的分类标准，汇编语言可以分为多种类型。按照指令集架构的不同，可以分为x86汇编、ARM汇编、MIPS汇编等。按照汇编语法风格，又可以分为Intel语法和AT&T语法。

#### 2.1.2 常用的汇编指令集

对于x86架构来说，最常用的指令集包括但不限于：
- 数据传输指令，例如`MOV`, `PUSH`, `POP`。
- 算术运算指令，如`ADD`, `SUB`, `MUL`, `DIV`。
- 逻辑运算指令，例如`AND`, `OR`, `XOR`, `NOT`。
- 控制转移指令，如`JMP`, `CALL`, `RET`。
- 字符串和内存操作指令，比如`MOVSB`, `STOSB`。

这些指令构成了汇编语言的基础，是进行更复杂编程任务的前提条件。

### 2.2 多位十进制数的表示方法

处理多位十进制数在汇编语言中是一项基础而重要的任务，通常涉及到进位和借位操作。

#### 2.2.1 二进制、八进制与十进制的转换

多位十进制数在计算机中通常以二进制形式存储。转换过程通常分为以下步骤：
- **二进制转十进制**：通过各二进制位对应的权重累加得到十进制数。
- **十进制转二进制**：将十进制数除以2，记录余数，再将商继续除以2，反复此过程直至商为0。
- **八进制转换**：可先将八进制数转换为十进制数，再从十进制转换为二进制，或者通过直接的位操作实现。

#### 2.2.2 十进制数的存储方式

在计算机中，十进制数可以采用不同的编码方式进行存储，常见的包括：
- **二进制编码的十进制数（BCD）**：每一个十进制数字用4位二进制表示，如十进制数`9`用二进制`1001`表示。
- **压缩BCD和未压缩BCD**：在未压缩BCD中，每个十进制数字占据一个字节；在压缩BCD中，两个十进制数字共享一个字节。

### 2.3 加法操作的基本原理

在汇编语言中，加法操作是基本的算术运算之一，其核心在于对二进制位的操作。

#### 2.3.1 二进制加法与进位机制

二进制加法的基本规则与十进制加法相似，但是进位发生在`1+1=10`的情况下，即向高位进一位。进位机制是多个位同时加法操作时保证计算正确性的关键。

#### 2.3.2 十进制加法的特殊处理（BCD加法）

对于BCD加法，由于每个十进制数字只用四位二进制表示，当两个BCD位相加结果大于`1001`时，需要调整为十进制的加法处理，并额外处理进位。

## 第三章：边界条件处理策略与实践

### 3.1 边界条件的定义与分类

边界条件是指在数据的处理、运算中所可能达到的极限状态或边界情形。对于加法操作，边界条件通常指可能导致运算错误或数据溢出的特殊情况。

#### 3.1.1 计算机中的边界条件概念

在计算机科学中，边界条件是指输入值或系统状态的特定值，这些值可能引起程序执行的某些行为与正常情况不同。这包括输入数据的最大最小值、数据类型所能表示的范围、循环次数的上下限等。

#### 3.1.2 边界条件在加法操作中的表现

在多位十进制加法中，边界条件可能表现为最大值加1造成的溢出、负数加法等。在处理这些情况时，程序员需要特别注意加法操作的正确性和溢出的正确处理。

### 3.2 十进制加法中的边界问题分析

多位十进制加法中常见的边界问题包括进位溢出和非十进制数的错误处理。

#### 3.2.1