MATLAB多项式拟合前沿技术与算法探索

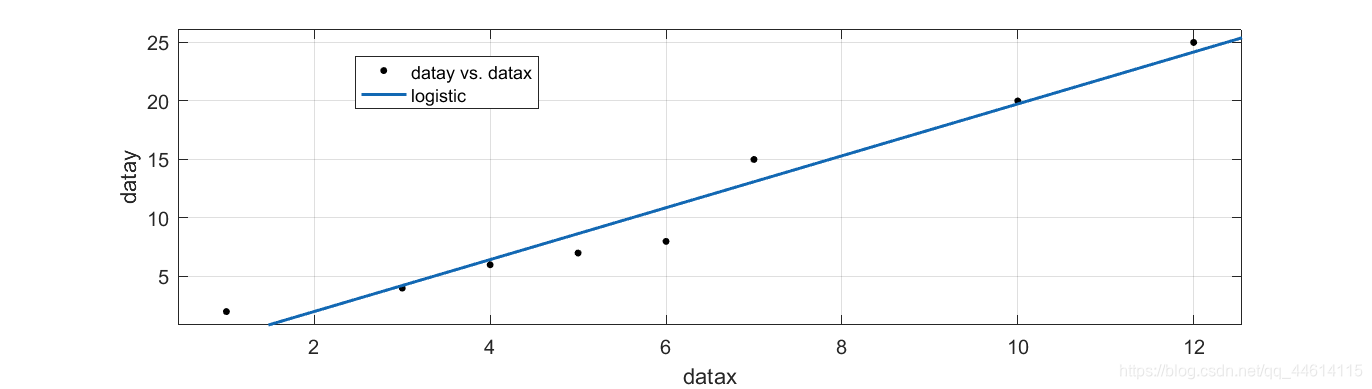
# 1. 多项式拟合概述**

多项式拟合是一种数学技术，用于通过一组数据点拟合一条多项式曲线。它广泛应用于各种领域，包括数据建模、预测分析和图像处理。

多项式曲线由以下方程定义：

f(x) = a_0 + a_1x + a_2x^2 + ... + a_nx^n

其中，a_0、a_1、...、a_n 是多项式的系数，n 是多项式的阶数。拟合的目标是找到一组系数，使多项式曲线与数据点尽可能接近。

# 2. 多项式拟合方法

### 2.1 传统方法

#### 2.1.1 最小二乘法

最小二乘法是一种广泛用于多项式拟合的传统方法。其目标是找到一组多项式系数，使得拟合曲线与给定数据点的平方误差之和最小。

**代码块：**

% 给定数据点
x = [1, 2, 3, 4, 5];
y = [2, 4, 6, 8, 10];

% 拟合一个二次多项式
p = polyfit(x, y, 2);

% 计算拟合曲线上的点
x_fit = linspace(min(x), max(x), 100);
y_fit = polyval(p, x_fit);

% 绘制拟合曲线和数据点
plot(x, y, 'o', x_fit, y_fit, '-');

**逻辑分析：**

* `polyfit` 函数使用最小二乘法拟合一个二次多项式，返回多项式系数 `p`。
* `polyval` 函数使用多项式系数 `p` 计算拟合曲线上的点。
* `plot` 函数绘制拟合曲线和原始数据点。

**参数说明：**

* `x`：数据点的自变量。
* `y`：数据点的因变量。
* `2`：拟合多项式的次数。
* `x_fit`：拟合曲线的自变量范围。
* `y_fit`：拟合曲线的因变量值。

#### 2.1.2 加权最小二乘法

加权最小二乘法是一种改进的最小二乘法，它允许为不同的数据点分配不同的权重。这对于处理具有不同可靠性的数据点非常有用。

**代码块：**

% 给定数据点和权重
x = [1, 2, 3, 4, 5];
y = [2, 4, 6, 8, 10];
w = [1, 2, 3, 4, 5];

% 拟合一个二次多项式
p = polyfit(x, y, 2, w);

% 计算拟合曲线上的点
x_fit = linspace(min(x), max(x), 100);
y_fit = polyval(p, x_fit);

% 绘制拟合曲线和数据点
plot(x, y, 'o', x_fit, y_fit, '-');

**逻辑分析：**

* `polyfit` 函数使用加权最小二乘法拟合一个二次多项式，返回多项式系数 `p`。
* `polyval` 函数使用多项式系数 `p` 计算拟合曲线上的点。
* `plot` 函数绘制拟合曲线和原始数据点。

**参数说明：**

* `w`：数据点的权重。

### 2.2 现代方法

#### 2.2.1 正则化方法

正则化方法在拟合多项式时引入了一个惩罚项，以防止过拟合。这通过限制多项式系数的大小来实现。

**代码块：**

% 给定数据点
x = [1, 2, 3, 4, 5];
y = [2, 4, 6, 8, 10]