MATLAB多项式拟合进阶指南：高阶拟合与误差分析

# 1. 多项式拟合基础**

多项式拟合是一种使用多项式函数对给定数据点进行建模的技术。它在科学、工程和金融等广泛领域中应用广泛，用于数据分析、预测和曲线拟合。

多项式函数的一般形式为：

f(x) = a_0 + a_1x + a_2x^2 + ... + a_nx^n

其中，a_0、a_1、...、a_n 为多项式系数，x 为自变量，n 为多项式的阶数。拟合过程的目标是找到一组系数，使得多项式函数与给定数据点的拟合程度最佳。

# 2. 高阶多项式拟合

### 2.1 高阶拟合的原理和方法

**2.1.1 不同拟合算法的比较**

高阶多项式拟合通常使用最小二乘法进行。最小二乘法通过最小化拟合曲线与原始数据的平方误差来确定拟合多项式的系数。

| 算法 | 优点 | 缺点 |
|---|---|---|
| 普通最小二乘法 (OLS) | 简单且易于实现 | 对异常值敏感 |
| 加权最小二乘法 (WLS) | 可处理具有不同权重的观测值 | 权重选择可能具有挑战性 |
| 正则化最小二乘法 (RLS) | 可防止过拟合 | 可能会引入偏差 |

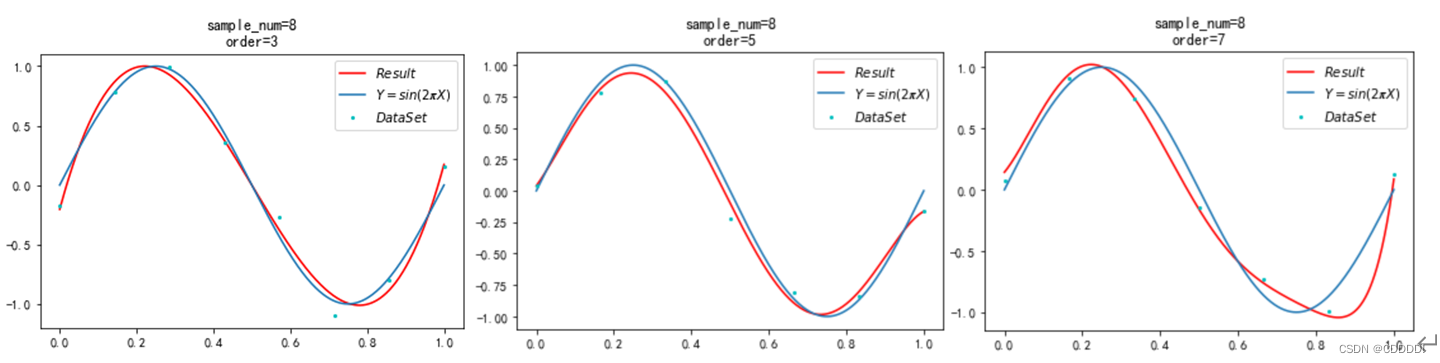
**2.1.2 拟合阶数的选择**

拟合阶数的选择对于高阶拟合至关重要。过低的阶数可能导致欠拟合，而过高的阶数可能导致过拟合。

* **欠拟合：**拟合曲线无法很好地拟合数据，导致较大的误差。
* **过拟合：**拟合曲线过度拟合数据，导致在训练集上表现良好但在新数据上表现不佳。

选择拟合阶数时，可以使用以下准则：

* **Akaike信息准则 (AIC)：**一种惩罚过拟合的准则，较低的AIC值表示更好的拟合。
* **贝叶斯信息准则 (BIC)：**另一种惩罚过拟合的准则，与AIC类似，但更严格。
* **交叉验证：**将数据分为训练集和测试集，并评估拟合模型在测试集上的性能。

### 2.2 高阶拟合的应用

**2.2.1 数据平滑和降噪**

高阶多项式拟合可用于平滑数据并去除噪声。通过拟合高阶多项式，可以捕获数据的整体趋势，同时滤除随机波动。

**2.2.2 曲线拟合和预测**

高阶多项式拟合可用于拟合复杂曲线并进行预测。通过拟合高阶多项式，可以获得数据的数学表示，并使用该表示来预测新数据点。

**代码块：**

% 数据导入和预处理
data = load('data.txt');
x = data(:, 1);
y = data(:, 2);

% 高阶多项式拟合
p = polyfit(x, y, 10);

% 拟合结果可视化
figure;
plot(x, y, 'o');
hold on;
plot(x, polyval(p, x), 'r-');
legend('原始数据', '拟合曲线');
xlabel('x');
ylabel('y');

% 误差分析
error = y - polyval(p, x);
fprintf('平均绝对误差 (MAE): %.2f\n', mean(abs(error)));
fprintf('均方根误差 (RMSE): %.2f\n', sqrt(mean(error.^2)));

**逻辑分析：**

* `polyfit()` 函数用于拟合高阶多项式，其中 `x` 为自变量，`y` 为因变量，`10` 为拟合阶数。
* `polyval()` 函数用于计算拟合曲线上给定自变量 `x` 的值。
* `mean()` 和 `sqrt()` 函数分别用于计算平均绝对误差 (MAE) 和均方根误差 (RMSE)。

# 3. 拟合误差分析

### 3.1 拟合误差的类型和度量

拟合误差衡量拟合模型与原始数据的偏差程度。在多项式拟合中，常用的误差度量包括：

**平均绝对误差（MAE）**

MAE 计算拟合模型预测值与真实值之间的绝对差值的平均值。它对异常值不敏感，但不能衡量误差的方向。

**均方根误差（RMSE）**

RMSE 计算拟合模型预测值与真实值之间的平方差值的平方根的平均值。它对异常值敏感，但可以衡量误差的方向。

### 3.2 误差分析的技巧

误差分析对于评估拟合模型的性能至关重要。以下是一些常用的技巧：

**残差图分析**

残差图将拟合模型的预测值与真实值之间的差值（残差）绘制在图形上。残差图可以帮助识别拟合模型的不足之处，例如：

* **线性残差图：**如果残差图呈现线性趋势，则表明拟合模型的阶数太低或存在非线性关系。
* **随机残差图：**如果残差图呈现随机分布，则表明拟合模型的阶数合适。
* **异方差残差图：**如果残差图呈现异方差（即残差的方差随着自变量的变化而变化），则表明拟合模型存在异方差问题。

**交叉验证**

交叉验证是一种评估拟合模型泛化能力的技术。它将数据集划分为训练集和测试集，并使用训练集拟合模型，然后使用测试集评估模型的性能。交叉验证可以帮助避免过拟合，即模型在训练集上表现良好但在新数据上表现不佳。

### 代码示例：拟合误差分析

% 导入数据
data = load('data.txt');
x = data(:, 1);
y = data(:, 2);

% 拟合多项式模型
p = polyfit(x, y, 5);

% 预测值
y_pred = polyval(p, x);

% 计算误差
mae = mean(abs(y_pred - y));
rmse = sqrt(mean((y_pred - y).^2));

% 绘制残差图
figure;
scatter(x, y_pred - y);
xlabel('x');
ylabel('Residual');
title('Residual Plot');

% 交叉验证
cv = cvpartition(length(x), 'KFold', 10);
rmse_cv = zeros(10, 1);
for i = 1:10
    train_idx = training(cv, i);
    test_idx = test(cv, i);
    p_train = polyfit(x(train_idx), y(train_idx), 5);
    y_pred_test = polyval(p_train, x(test_idx));
    rmse_cv(i) = sqrt(mean((y_pred_test - y(test_idx)).^2));
end

% 计算交叉验证的平均RMSE
rmse_cv_avg = mean(rmse_cv);

**逻辑分析：**

* 代码首先导入数据并拟合多项式模型。
* 然后计算MAE和RMSE作为拟合误差的度量。
* 残差图绘制拟合模型预测值与真实值之间的差值。
* 交叉验证将数据集划分为训练集和测试集，并计算训练集和测试集上的RMSE。
* 最后，计算交叉验证的平均RMSE作为拟合模型泛化能力的度量。

# 4. MATLAB中高阶多项式拟合实践

### 4.1 MATLAB中拟合函数的使用

MATLAB提供了丰富的函数库，用于多项式拟合。其中，`polyfit()`和`polyval()`函数是两个常用的函数。

#### 4.1.1 polyfit() 函数

`polyfit()`函数用于拟合给定数据点的一组多项式系数。其语法如下：

p = polyfit(x, y, n)

其中：

- `x`：自变量数据点。
- `y`：因变量数据点。
- `n`：拟合多项式的阶数。

`polyfit()`函数返回一个长度为`n+1`的向量`p`，其中包含多项式系数。这些系数按降幂排列，即`p(1)`是最高次项的系数，`p(end)`是常数项的系数。

#### 4.1.2 polyval() 函数

`polyval()`函数用于计算给定多项式系数和自变量值的多项式值。其语法如下：

y = polyval(p, x)

其中：

- `p`：多项式系数向量。
- `x`：自变量值。

`polyval()`函数返回一个与`x`同维度的向量`y`，其中包含计算出的多项式值。

### 4.2 高阶拟合的代码示例

下面是一个高阶多项式拟合的代码示例：

% 数据导入和预处理
data = load('data.txt');
x = data(:, 1);
y = data(:, 2);

% 高阶多项式拟合
n = 5;  % 拟合阶数
p = polyfit(x, y, n);

% 拟合结果可视化和误差分析
y_fit = polyval(p, x);
figure;
plot(x, y, 'o', 'MarkerSize', 8);
hold on;
plot(x, y_fit, '-', 'LineWidth', 2);
xlabel('x');
ylabel('y');
legend('Data', 'Fitted Curve');
title('High-Order Polynomial Fit');

% 计算拟合误差
mae = mean(abs(y - y_fit));
rmse = sqrt(mean((y - y_fit).^2));
fprintf('Mean Absolute Error (MAE): %.4f\n', mae);
fprintf('Root Mean Squared Error (RMSE): %.4f\n', rmse);

**代码逻辑分析：**

1. 导入数据并将其存储在`x`和`y`变量中。
2. 使用`polyfit()`函数拟合一个5阶多项式，并将其系数存储在`p`变量中。
3. 使用`polyval()`函数计算拟合曲线的值，并将其存储在`y_fit`变量中。
4. 绘制原始数据和拟合曲线，并显示拟合误差。

**参数说明：**

- `data.txt`：包含自变量和因变量数据的文本文件。
- `n`：拟合多项式的阶数。
- `mae`：平均绝对误差，衡量拟合曲线与原始数据的平均绝对偏差。
- `rmse`：均方根误差，衡量拟合曲线与原始数据的均方根偏差。

# 5. 进阶应用

### 5.1 多项式拟合在机器学习中的应用

#### 5.1.1 回归模型

多项式拟合可用于构建回归模型，用于预测连续目标变量。通过拟合数据点到高阶多项式，可以捕获数据的非线性关系。

% 导入数据
data = load('data.csv');
X = data(:, 1); % 特征
y = data(:, 2); % 目标

% 拟合高阶多项式
p = polyfit(X, y, 5);

% 预测新数据
new_X = linspace(min(X), max(X), 100);
new_y = polyval(p, new_X);

% 绘制拟合曲线和数据点
plot(X, y, 'o', new_X, new_y, '-');
legend('数据点', '拟合曲线');

#### 5.1.2 分类模型

多项式拟合也可用于构建分类模型，用于预测离散目标变量。通过将数据点拟合到高阶多项式，可以创建决策边界，将数据点划分为不同的类别。

% 导入数据
data = load('data.csv');
X = data(:, 1:2); % 特征
y = data(:, 3); % 类别标签

% 拟合高阶多项式
model = fitcsvm(X, y, 'KernelFunction', 'polynomial', 'PolynomialOrder', 3);

% 预测新数据
new_X = [linspace(min(X(:, 1)), max(X(:, 1)), 100), linspace(min(X(:, 2)), max(X(:, 2)), 100)];
new_y = predict(model, new_X);

% 绘制决策边界和数据点
gscatter(X(:, 1), X(:, 2), y);
hold on;
plot(new_X(:, 1), new_X(:, 2), 'o', 'MarkerFaceColor', 'none', 'MarkerEdgeColor', 'red');
legend('数据点', '决策边界');

### 5.2 多项式拟合在图像处理中的应用

#### 5.2.1 图像增强

多项式拟合可用于图像增强，例如平滑和锐化。通过拟合图像像素到高阶多项式，可以去除噪声并增强图像细节。

% 导入图像
image = imread('image.jpg');

% 拟合高阶多项式
p = polyfit(1:size(image, 1), double(image(:, 1)), 5);

% 增强图像
enhanced_image = polyval(p, 1:size(image, 1));

% 显示原始图像和增强图像
subplot(1, 2, 1);
imshow(image);
title('原始图像');

subplot(1, 2, 2);
imshow(enhanced_image);
title('增强图像');

#### 5.2.2 图像分割

多项式拟合可用于图像分割，例如提取图像中的特定对象。通过拟合图像像素到高阶多项式，可以创建分割边界，将图像划分为不同的区域。

% 导入图像
image = imread('image.jpg');

% 拟合高阶多项式
p = polyfit(1:size(image, 1), double(image(:, 1)), 5);

% 分割图像
segmented_image = zeros(size(image));
for i = 1:size(image, 1)
    segmented_image(i, :) = polyval(p, i) > mean(double(image(:, 1)));
end

% 显示原始图像和分割图像
subplot(1, 2, 1);
imshow(image);
title('原始图像');

subplot(1, 2, 2);
imshow(segmented_image);
title('分割图像');