MATLAB多项式拟合与其他拟合方法大PK：优势与局限

# 1. 拟合方法概述

拟合是一种数学技术，用于找到一条曲线或曲面，以最适合给定的一组数据点。拟合方法有多种，每种方法都有其优点和缺点。

拟合方法通常根据其复杂程度进行分类。线性拟合是拟合最简单的方法，它使用一条直线来拟合数据点。多项式拟合比线性拟合更复杂，它使用多项式函数来拟合数据点。非线性拟合是最复杂的方法，它使用非线性函数来拟合数据点。

# 2. MATLAB 多项式拟合

### 2.1 多项式拟合的基本原理

多项式拟合是一种通过寻找一条多项式曲线来近似一组数据的过程。多项式的阶数决定了曲线的复杂程度，阶数越高，曲线越能紧密地拟合数据。

**多项式方程的一般形式为：**

y = a0 + a1x + a2x^2 + ... + anx^n

其中：

* `y` 是因变量
* `x` 是自变量
* `a0`, `a1`, ..., `an` 是多项式的系数

### 2.2 MATLAB 中的多项式拟合函数

MATLAB 提供了 `polyfit` 函数进行多项式拟合。该函数的语法如下：

p = polyfit(x, y, n)

其中：

* `x` 是自变量数据向量
* `y` 是因变量数据向量
* `n` 是多项式的阶数

`polyfit` 函数返回一个包含多项式系数的向量 `p`。

### 2.3 多项式拟合的优缺点

**优点：**

* **简单且易于实现：**多项式拟合是一种直观的拟合方法，易于理解和实现。
* **适用于各种数据：**多项式拟合可以用于拟合各种类型的数据，包括线性、非线性和周期性数据。
* **可解释性强：**多项式的系数可以提供有关数据趋势和模式的见解。

**缺点：**

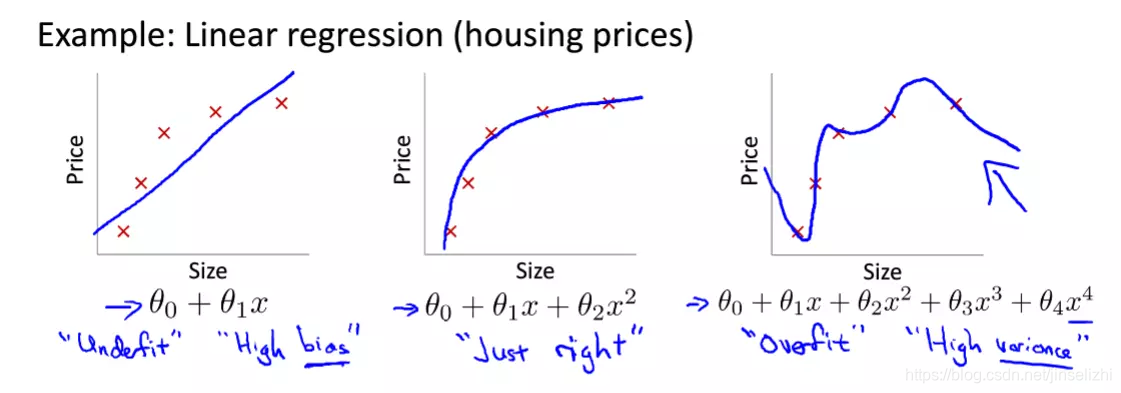
* **可能出现过拟合：**高阶多项式可能会过拟合数据，导致模型在训练数据上表现良好，但在新数据上泛化能力差。
* **数值不稳定：**高阶多项式的系数可能对数据中的噪声非常敏感，导致数值不稳定。
* **计算成本高：**高阶多项式的拟合需要大量的计算资源。

**代码示例：**

% 数据生成
x = linspace(-1, 1, 100);
y = sin(x) + 0.1 * randn(size(x));

% 多项式拟合
n = 5;
p = polyfit(x, y, n);

% 拟合曲线可视化
figure;
plot(x, y, 'o');
hold on;
plot(