资源优化中的背包算法应用：成本效益分析深度解析

# 1. 背包问题的理论基础

## 1.1 背包问题的起源与定义

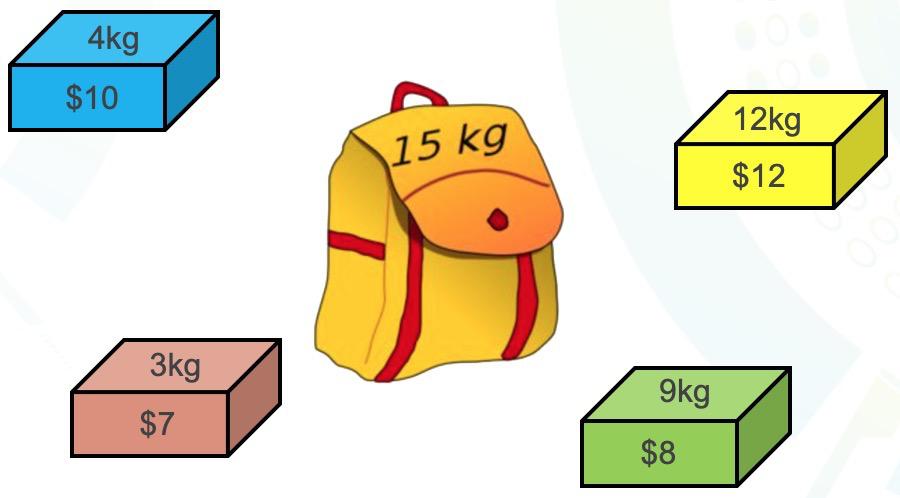
背包问题源自于一个简单的概念：给定一组物品，每个物品都有其重量和价值，在限定的总重量内，如何选择装入背包的物品以最大化其总价值。这个问题简单直观，却蕴含着丰富的问题结构，是组合优化领域中一个典型的问题。

## 1.2 背包问题的分类

背包问题根据其限制条件可以被分为多种类型，比如0-1背包问题、分数背包问题、多维背包问题等。其中，0-1背包问题规定每个物品只能选择装入或不装入背包，而分数背包问题则允许物品被分割，可以装入背包的一部分。

## 1.3 背包问题的研究意义

背包问题作为运筹学中的一种基本问题，在实际应用中具有广泛的影响。它不仅能够用于解决实际中的资源分配问题，而且对算法设计和计算复杂性理论的研究都有着重要的推动作用，是理解许多复杂问题本质的基石。

这个章节通过介绍背包问题的起源、分类及研究意义，为读者提供了一个关于背包问题的全面概述。接下来，我们将深入探讨经典背包问题及其解法，进一步理解这一领域的理论基础和实践应用。

# 2. 经典背包问题及其解法

### 0-1背包问题的理论模型

#### 背包问题的定义与分类

背包问题是一类组合优化的问题。在最简单的形式中，它包含了需要在限定的总重量（或其他资源限制）内选择物品，以最大化其总价值或总重量。在经典算法中，背包问题通常分为两大类：0-1背包问题和分数背包问题。

0-1背包问题是最基本的形式，其中的每一个物品只能被选中一次（即取或不取，0或1），不能分割。这与现实世界中的情况十分吻合，例如选择是否带上某件物品，但不能带上部分。0-1背包问题被广泛地研究和应用，因为它代表了许多实际情况中的选择问题，比如旅行中行李的打包、资源分配和项目选取等。

#### 动态规划法求解0-1背包问题

动态规划是解决0-1背包问题的一个有效算法。其基本思想是，将一个大问题分解为若干个规模较小的相似问题，按步骤求解并存储子问题的解，避免重复计算。

在动态规划中，一个关键的步骤是构建一个表，通常是二维的，来保存子问题的解。对于0-1背包问题，我们可以定义一个二维数组`dp[i][w]`，表示考虑前`i`个物品时，面对`w`重量限制能否取到最大价值。状态转移方程如下：

dp[i][w] = max(dp[i-1][w], dp[i-1][w - weights[i]] + values[i]) if weights[i] <= w
dp[i][w] = dp[i-1][w] otherwise

这里，`weights[i]`和`values[i]`分别表示第`i`个物品的重量和价值。通过这个方程，我们可以逐步填充表格，直到得到`dp[n][W]`，即所有物品考虑完毕，面对总重量`W`时的最大价值。

代码实现可能如下：

def knapsack_01(weights, values, W):
    n = len(values)
    dp = [[0 for x in range(W + 1)] for x in range(n + 1)]

    for i in range(1, n + 1):
        for w in range(1, W + 1):
            if weights[i-1] <= w:
                dp[i][w] = max(dp[i-1][w], dp[i-1][w-weights[i-1]] + values[i-1])
            else:
                dp[i][w] = dp[i-1][w]
    return dp[n][W]

#### 分数背包问题与贪心算法

分数背包问题与0-1背包问题类似，但是其中的物品可以分割成更小的部分。在分数背包问题中，物品可以取任意比例，而不是只有0或1。

### 分数背包问题与贪心算法

#### 分数背包问题的介绍

分数背包问题中，每一个物品可以取出一部分，而不是只能全取或全不取。这使得分数背包问题的解法与0-1背包问题的求解策略有所不同。

在分数背包问题中，可以使用贪心策略进行求解。贪心策略的思路是，按照某种排序选择物品，依次添加至背包中，直到背包无法再添加更多的物品为止。这种策略的正确性基于物品单位价值（即价值除以重量）的优化，我们应首先选取单位价值最高的物品添加至背包中。

#### 贪心算法的应用与局限性

贪心算法在分数背包问题中的应用非常直接。算法的实现步骤如下：

1. 计算所有物品的单位价值。
2. 将物品按单位价值从高到低排序。
3. 按排序好的顺序选择物品，将能够放入背包的尽可能多的部分加入背包，直到无法再增加为止。

贪心算法的优势在于它的简单性和执行速度，但它的局限性在于并不总是能够得到最优解。尤其是对于某些特殊的背包问题实例，贪心算法可能只返回接近最优但不是最优的解。

def fractional_knapsack(values, weights, W):
    # 创建物品列表，每个物品为一个元组(value, weight)
    items = list(zip(values, weights))
    # 按单位价值降序排序物品
    items.sort(key=lambda x: x[0]/x[1], reverse=True)

    total_value = 0
    for value, weight in items:
        if W >= weight:
            # 如果背包能装下整个物品
            W -= weight
            total_value += value
        else:
            # 只装下部分物品
            fraction = W / weight
            total_value += value * fraction
            break
    return total_value

#### 贪心算法的应用与局限性

### 背包问题的变种及其挑战

#### 多维背包问题分析

多维背包问题是在经典背包问题基础上的一个扩展，其中背包和物品不仅有一个容量限制，而是有限制的维度。例如，除了重量外，可能还有体积、成本等限制因素。

解决多维背包问题的方法有多种，包括回溯法、分支定界法和动态规划法等。动态规划依然是一个常见的选择，但需要注意的是，其状态转移方程和表格填充过程更为复杂。

#### 背包问题的NP完全性

背包问题在某些变种下是NP完全问题（例如在有多种物品类型或多个背包时）。这意味着找到多项式时间内的解决方案是极其困难的，甚至可能是不存在的。

NP完全问题的研究在计算机科学中非常关键，它推动了近似算法和启发式算法的发展，这些算法可以快速找到问题的可接受解，尽管这些解可能不是最优的。

在面对NP完全问题时，计算机科学家通常寻找可以在合理时间内解决问题的近似算法或启发式算法。这些算法不是寻求精确解，而是寻求一个接近最优解的快速可行解，例如通过贪心策略、遗传算法、模拟退火等方法。

综上所述，背包问题不仅在理论上具有挑战性，而且在实际应用中也非常重要。它的多样性和复杂性使其成为算法研究的一个重要领域，同时也为解决现实世界中的优化问题提供了强有力的理论工具。

# 3. 背包算法在成本效益分析中的应用

在面对有限资源和多个项目选择时，成本效益分析（Cost-Benefit Analysis, CBA）帮助决策者权衡各种方案的利弊，最终做出经济合理的选择。背包问题作为一种资源优化模型，在成本效益分析中拥有广泛应用，特别是在资源分配、多目标决策问题中，可以提供科学的决策支持。本章将详细介绍背包算法在成本效益分析中的应用。

## 3.1 成本效益分析概述

### 3.1.1 成本效益分析的定义与重要性

成本效益分析（CBA）是一种比较项目或政策的总成本与总效益的方法，以评估其是否值得投资的决策工具。它将涉及的所有成本（包括直接成本、间接成本、机会成本等）和收益（包括直接收益、间接收益、社会效益等）货币化，以便于进行量化比较。CBA的重要性在于，它为评估项目价值提供了一个客观标准，有助于实现资源的最优分配。

### 3.1.2 经典的成本效益分析模型

经典的成本效益分析模型包含以下核心步骤：

1. 确定分析范围：明确分析的项目边界、参与方以及时间跨度。
2. 识别成本与收益：列出所有相关的成本和收益。
3. 货币化评估：将所有的成本和收益转化为货币值。
4. 计算净现值（NPV）：通过折现率将未来的成本和收益转化为当前价值，并计算净现值。
5. 敏感性分析：评估参数变化对结果的影响。
6. 决策：基于CBA结果，决定是否进行项目投资。

## 3.2 背包算法优化资源分配

### 3.2.1 背包模型在资源优化中的应用

背包模型将资源分配问题抽象为背包中物品的最优组合选择问题。每一个物品代表一个项目，其重量代表项目成本，价值代表项目收益。背包模型在资源优化中的应用过程大致如下：

1. 识别项目和资源：定义所有潜在的项目（物品）以及可用的资源（背包容量）。
2. 评估成本与收益：为每个项目确定成本和预期收益。
3. 构建背包模型：将问题转化为背包问题的数学模型。
4. 求解模型：采用动态规划等算法，计算出最优的项目组合。
5. 应用结果：根据求解结果制定资源分配计划。

### 3.2.2 实际案例分析：资源分配优化

以一家科技公司投资决策为例，公司有限的预算需要在多个研发项目之间进行分配。利用背包算法，可以得到最大化公司预期收益的项目组合。

假设公司有三个研发项目A、B、C，预算上限为1000万元。项目收益与成本如下：

| 项目 | 成本（万元） | 预期收益（万元） |
|------|-------------