哈希表如何应对频繁的插入和删除操作？

# 2. 哈希表的基本原理和实现

哈希表是一种数据结构，它使用哈希函数将键映射到值。哈希函数是一个将键转换为固定大小数组索引的函数。通过使用哈希函数，哈希表可以快速查找、插入和删除元素，而无需遍历整个表。

哈希表的基本原理是：

1. **哈希函数：**哈希函数将键映射到一个固定大小数组的索引。
2. **哈希冲突：**当多个键映射到同一个索引时，就会发生哈希冲突。
3. **冲突处理：**哈希表使用冲突处理方法来解决冲突，例如开放寻址法或链地址法。

# 2. 哈希表的基本原理和实现

哈希表是一种数据结构，它使用哈希函数将键映射到值。哈希函数是一个将任意长度的输入映射到固定长度输出的函数。哈希表的基本原理是通过哈希函数将键映射到数组索引，从而实现快速查找和插入操作。

### 2.1 哈希函数的选取和设计

哈希函数的选取对哈希表性能至关重要。一个好的哈希函数应该具有以下特性：

- **均匀性：**将键均匀地分布在哈希表中，避免哈希冲突。
- **确定性：**对于相同的键，总是产生相同的哈希值。
- **快速计算：**哈希函数的计算应该足够快，以避免影响哈希表性能。

常见的哈希函数包括：

- **模运算：**将键对一个素数取模，得到哈希值。
- **平方取中：**将键平方，取中间几位作为哈希值。
- **斐波那契哈希：**将键与一个斐波那契数相乘，取结果的低位作为哈希值。

### 2.2 哈希冲突的处理方法

哈希冲突是指不同的键映射到相同的哈希值。处理哈希冲突的方法有以下几种：

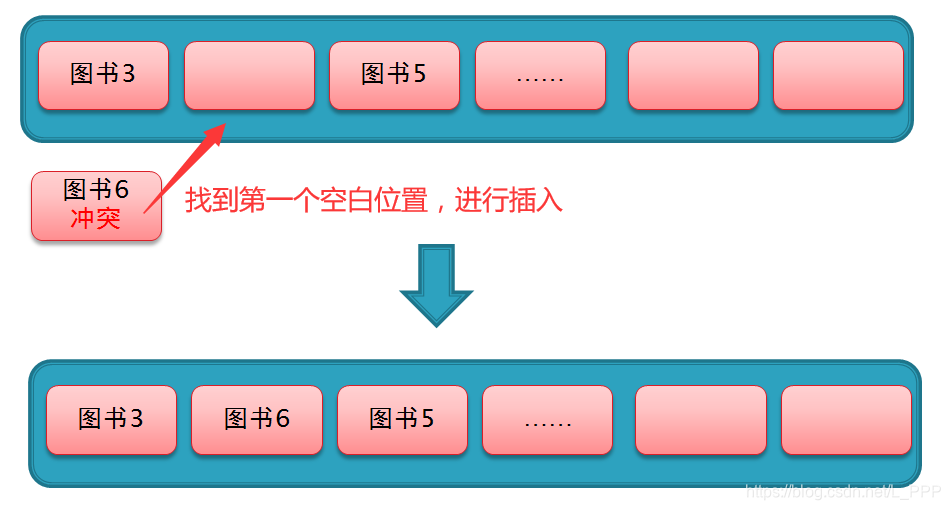
#### 2.2.1 开放寻址法

开放寻址法将冲突的键存储在哈希表中相邻的空位置。常用的开放寻址法包括：

- **线性探测：**从冲突的位置开始，线性地查找下一个空位置。
- **二次探测：**从冲突的位置开始，以二次递增的步长查找下一个空位置。
- **双哈希法：**使用两个哈希函数，如果第一个哈希函数冲突，则使用第二个哈希函数查找下一个空位置。

#### 2.2.2 链地址法

链地址法将冲突的键存储在哈希表中与冲突位置关联的链表中。链地址法可以有效地解决哈希冲突，但会增加空间开销。

#### 2.2.3 双哈希法

双哈希法使用两个哈希函数，第一个哈希函数确定冲突位置，第二个哈希函数确定在冲突位置存储键的偏移量。双哈希法可以有效地解决哈希冲突，并且比开放寻址法具有更好的性能。

### 代码示例

以下 Python 代码展示了使用开放寻址法处理哈希冲突的哈希表实现：

class HashTable:
    def __init__(self, size):
        self.table = [None] * size

    def hash_function(self, key):
        return key % len(self.table)

    def insert(self, key, value):
        index = self.hash_function(key)
        while self.table[index] is not None:
            index = (index + 1) % len(self.table)
        self.table[index] = (key, value)

    def search(self, key):