理解哈希碰撞及解决方法

# 1. 哈希函数与哈希碰撞**

哈希函数是一种将任意长度的数据映射到固定长度输出的函数，输出称为哈希值。哈希函数具有单向性，即给定一个哈希值，无法逆向推导出原始数据。哈希碰撞是指不同的输入数据映射到相同的哈希值的情况。

# 2. 哈希碰撞的成因与影响

哈希碰撞是指不同的输入数据经过哈希函数计算后得到相同的哈希值的情况。它在哈希表等数据结构中是一个常见的现象，会对哈希表的性能和可靠性产生一定的影响。

### 2.1 哈希函数的局限性

哈希函数将任意长度的输入数据映射到固定长度的哈希值，这本质上是一个不可逆的过程。因此，对于任何哈希函数，都存在着哈希碰撞的可能性。

哈希函数的局限性主要体现在以下两个方面：

- **有限的哈希空间：**哈希值是固定长度的，因此哈希空间是有限的。当输入数据的数量超过哈希空间的容量时，必然会发生哈希碰撞。
- **均匀分布的假设：**哈希函数通常假设输入数据是均匀分布的。然而，在实际应用中，输入数据往往具有非均匀分布，这会增加哈希碰撞的概率。

### 2.2 输入数据的分布和冲突概率

输入数据的分布对哈希碰撞的概率有很大的影响。如果输入数据分布均匀，则哈希碰撞的概率较低。反之，如果输入数据分布不均匀，则哈希碰撞的概率较高。

为了量化输入数据分布对哈希碰撞概率的影响，我们引入**冲突概率**的概念。冲突概率是指在给定哈希函数和哈希表大小的情况下，两个随机输入数据发生哈希碰撞的概率。

冲突概率可以用以下公式计算：

冲突概率 = 1 - (1 - 1/m)^n

其中：

- m 是哈希表的容量
- n 是输入数据的数量

从公式中可以看出，冲突概率与哈希表的容量和输入数据的数量成正比。这意味着，哈希表容量越小或输入数据数量越多，冲突概率就越高。

此外，冲突概率还与哈希函数的质量有关。一个好的哈希函数应该能够将输入数据均匀地分布在哈希空间中，从而降低冲突概率。

# 3.1 开放寻址法

开放寻址法是一种解决哈希碰撞的方法，其基本思想是在哈希表中留出额外的空间来存储发生碰撞的元素。当发生碰撞时，它不会像链地址法那样将元素存储在链表中，而是直接在哈希表中寻找下一个空闲位置来存储该元素。

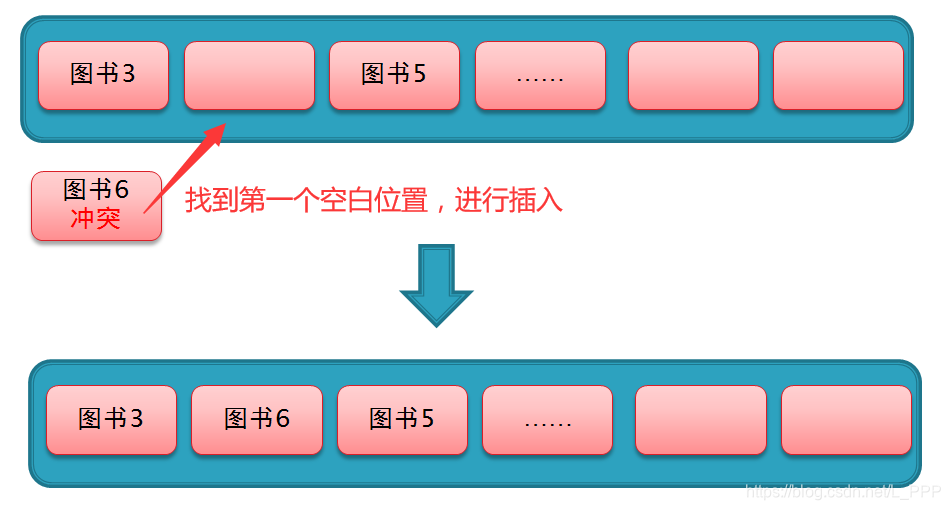
#### 3.1.1 线性探测

线性探测是最简单的开放寻址法。当发生碰撞时，它从碰撞位置开始，依次探测哈希表中的下一个位置，直到找到一个空闲位置来存储该元素。

def linear_probing(hash_table, key, value):
    index = hash(key) % len(hash_table)
    while hash_table[index] is not None:
        index = (index + 1) % len(hash_table)
    hash_table[index] = (key, value)

**逻辑分析：**

该代码实现了线性探测法。它首先计算键的哈希值，然后将哈希值对哈希表长度取模得到初始索引。如果该索引位置已被占用，则依次探测哈希表中的下一个位置，直到找到一个空闲位置。最后，将键值对存储在找到的空闲位置。

#### 3.1.2 二次探测

二次探测是另一种开放寻址法，与线性探测类似，但它在探测哈希表时采用二次探测序列。二次探测序列通常为 `1^2, 2^2, 3^2, ...`，即从 1 开始，每次探测的步长增加 1。

def quadratic_probing(hash_table, key, value):
    index = hash(key) % len(hash_table)
    i = 1
    while hash_table[index] is not None:
        index = (index + i**2) % len(hash_table)
        i += 1
    hash_table[index] = (key, value)

**逻辑分析：**

该代码实现了二次探测法。它首先计算键的哈希值，然后将哈希值对哈希表长度取模得到初始索引。如果该索引位置已被占用，则根据二次探测序列依次探测哈希表中的下一个位置，直到找到一个空闲位置。最后，将键值对存储在找到的空闲位置。

#### 3.1.3 双重哈希

双重哈希是一种更高级的开放寻址法，它使用两个不同的哈希函数来探测哈希表。当发生碰撞时，它使用第一个哈希函数计算初始索引，然后使用第二个哈希函数计算探测步长。

def double_hashing(hash_table, key, value):
    index1 = hash(key) % len(hash_table)
    index2 = hash(key, 2) % len(hash_table)
    i = 1
    while hash_table[index1] is not None:
        index1 = (index1 + i * index2) % len(hash_table)
        i += 1
    hash_table[index1] = (key, value)

**逻辑分析：**

该代码实现了双重哈希法。它首先计算键的两个哈希值，然后使用第一个哈希值计算初始索引，使用第二个哈希值计算探测步长。如果初始索引位置已被占用，则根据探测步长依次探测哈希表中的下一个位置，直到找到一个空闲位置。最后，将键值对存储在找到的空闲位置。

# 4. 哈希碰撞在实际应用中的实践

哈希碰撞在实际应用中有着广泛的应用，从数据库索引到密码学，再到分布式系统。本节将探讨哈希碰撞在这些领域的具体实践。

### 4.1 数据库中的哈希索引

哈希索引是一种数据结构，它使用哈希函数将数据映射到索引键。当需要查找数据时，哈希函数将查询键映射到索引键，然后直接访问相应的索引项。这种方法可以大大提高查询效率，尤其是在数据量较大的情况下。

**优点：**

* 快速查找：哈希索引可以快速查找数据，时间复杂度为 O(1)。
* 节省空间：哈希索引比 B 树索引占用更少的空间，因为它们不需要存储数据本身。
* 避免排序：哈希索引不需要对数据进行排序，这可以节省大量时间。

**缺点：**

* 哈希碰撞：哈希碰撞可能会导致数据丢失或不一致。
* 无法范围查询：哈希索引无法进行范围查询，因为数据不是按顺序存储的。

### 4.2 密码学中的哈希碰撞攻击

哈希碰撞在密码学中也扮演着重要角色。哈希函数用于生成消息摘要，该摘要是消息的唯一标识。如果攻击者能够找到两个具有相同哈希值的不同消息，则称为哈希碰撞攻击。

**攻击方法：**

* **生日攻击：**攻击者生成大量消息，并计算它们的哈希值。根据生日悖论，随着消息数量的增加，找到哈希碰撞的概率也会增加。
* **伪造攻击：**攻击者利用哈希碰撞来伪造数字签名或其他加密操作。

**防御措施：**

* 使用安全的哈希函数：选择具有高抗碰撞性的哈希函数，例如 SHA-256 或 SHA-512。
* 增加哈希值长度：增加哈希值长度可以降低哈希碰撞的概率。
* 使用盐值：在消息中添加随机盐值可以使攻击者更难找到哈希碰撞。

### 4.3 分布式系统中的哈希一致性

在分布式系统中，哈希碰撞可以用于实现数据的一致性。哈希一致性算法将数据分布在多个节点上，并使用哈希函数将每个数据项映射到一个特定的节点。

**工作原理：**

* **哈希环：**哈希环是一个虚拟环，每个节点在环上占据一个位置。
* **数据映射：**每个数据项都映射到哈希环上的一个位置。
* **数据存储：**数据存储在哈希环上负责该位置的节点上。

**优点：**

* 数据一致性：哈希一致性算法确保数据在所有节点上保持一致，即使某个节点发生故障。
* 可扩展性：哈希环可以动态扩展或缩小，以适应不断变化的负载。
* 容错性：哈希一致性算法可以容忍单个节点的故障，而不会丢失数据。

**缺点：**

* 哈希碰撞：哈希碰撞可能会导致数据丢失或不一致。
* 数据迁移：当添加或删除节点时，需要重新映射数据，这可能会导致性能下降。

# 5. 哈希碰撞的优化与展望

哈希碰撞虽然无法完全避免，但可以通过优化哈希函数和哈希表大小来降低其发生概率，提高哈希表的性能。

### 5.1 哈希函数的改进

哈希函数的质量直接影响哈希碰撞的概率。理想的哈希函数应该具有以下特性：

- **均匀性：**输入数据的不同值映射到哈希表不同位置的概率相等。
- **抗碰撞性：**不同的输入数据映射到相同哈希值（即碰撞）的概率极低。

为了提高哈希函数的质量，可以采用以下方法：

- **使用高质量的哈希算法：**如 MD5、SHA-256 等。
- **结合多个哈希函数：**将多个哈希函数的输出值进行组合，提高抗碰撞性。
- **随机化哈希函数：**在哈希函数中引入随机因子，降低碰撞概率。

### 5.2 哈希表大小的优化

哈希表的大小也会影响哈希碰撞的概率。哈希表过小会导致哈希碰撞频繁，而哈希表过大则会浪费空间。

理想的哈希表大小应满足以下条件：

- **装载因子：**哈希表中已存储元素的数量与哈希表大小的比值。装载因子过高会导致哈希碰撞频繁，而装载因子过低则会浪费空间。一般情况下，装载因子建议保持在 0.7 左右。
- **哈希表大小：**根据装载因子和已存储元素的数量计算哈希表大小。

hash_table_size = int(num_elements / load_factor)

### 5.3 未来哈希碰撞解决方法的研究

哈希碰撞的研究是一个持续进行的领域。未来可能出现以下解决方法：

- **量子哈希：**利用量子计算的特性，设计出更加抗碰撞的哈希函数。
- **基于机器学习的哈希：**利用机器学习算法，学习输入数据的分布并设计出更优的哈希函数。
- **分布式哈希：**将哈希表分布在多个节点上，降低单个节点上的哈希碰撞概率。