揭秘MATLAB图像锐化滤波器：高斯滤波、拉普拉斯滤波、Sobel滤波，让图像更清晰

# 1. MATLAB图像锐化滤波概述

图像锐化滤波是一种图像处理技术，用于增强图像中细节和边缘的清晰度。MATLAB提供了一系列图像锐化滤波器，包括高斯滤波、拉普拉斯滤波和Sobel滤波。这些滤波器使用不同的数学运算来处理图像，产生不同的锐化效果。

本章将概述MATLAB图像锐化滤波的基本原理和概念。我们将讨论每种滤波器的优点和缺点，并提供有关如何在MATLAB中使用它们的指导。通过理解图像锐化滤波器的基础知识，您可以有效地使用它们来增强图像的质量并提取有价值的信息。

# 2. 高斯滤波理论与实践

### 2.1 高斯滤波的原理和公式

#### 2.1.1 高斯核的生成

高斯滤波是一种线性平滑滤波器，其核心思想是使用高斯核对图像进行卷积运算。高斯核是一个对称的钟形曲线，其权重随着与中心点的距离呈指数衰减。

生成高斯核的公式为：

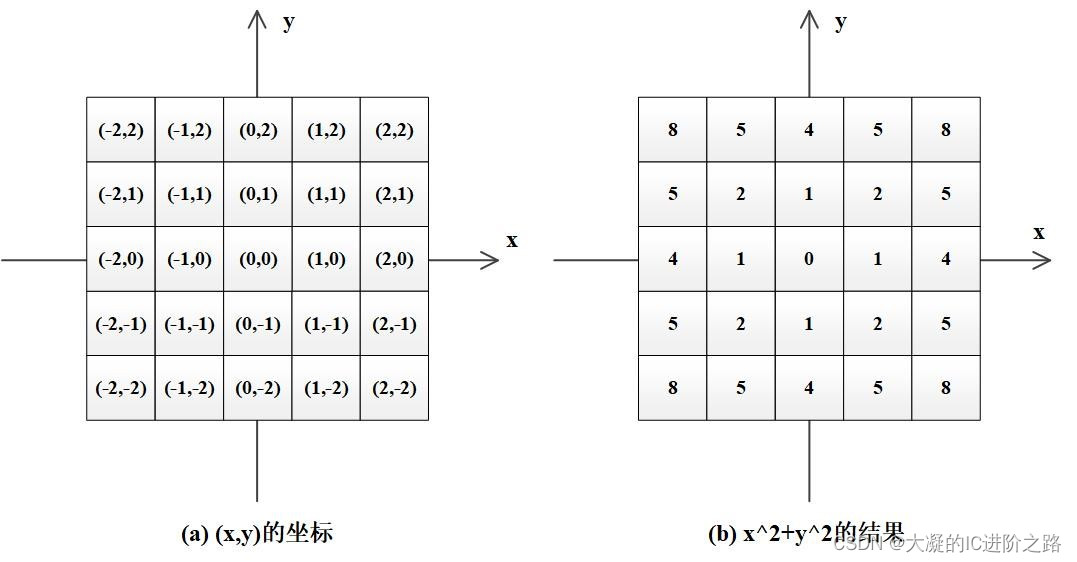
G(x, y) = (1 / (2πσ^2)) * e^(-(x^2 + y^2) / (2σ^2))

其中：

* `G(x, y)` 是高斯核在点 `(x, y)` 处的权重
* `σ` 是高斯核的标准差，控制高斯核的平滑程度

#### 2.1.2 高斯滤波的数学推导

高斯滤波的数学推导过程如下：

1. 将图像表示为一个二维矩阵 `I(x, y)`。
2. 创建一个高斯核 `G(x, y)`。
3. 对图像进行卷积运算：

I'(x, y) = I(x, y) * G(x, y)

其中：

* `I'(x, y)` 是滤波后的图像
* `*` 表示卷积运算

### 2.2 高斯滤波在图像锐化中的应用

#### 2.2.1 高斯滤波的卷积实现

在 MATLAB 中，可以使用 `imfilter` 函数对图像进行高斯滤波：

I_filtered = imfilter(I, G);

其中：

* `I` 是原始图像
* `G` 是高斯核
* `I_filtered` 是滤波后的图像

#### 2.2.2 高斯滤波的参数选择

高斯滤波的参数是高斯核的标准差 `σ`。较小的 `σ` 值产生更平滑的滤波效果，而较大的 `σ` 值产生更锐利的滤波效果。

选择 `σ` 值时需要考虑以下因素：

* 图像的噪声水平：较高的噪声水平需要较大的 `σ` 值。
* 图像的细节程度：较精细的细节需要较小的 `σ` 值。

一般来说，`σ` 值的范围在 0.5 到 2 之间。

# 3. 拉普拉斯滤波理论与实践

### 3.1 拉普拉斯滤波的原理和公式

#### 3.1.1 拉普拉斯算子的定义

拉普拉斯算子是一个二阶微分算子，用于检测图像中的二阶导数。它可以定义为：

∇²f(x, y) = ∂²f(x, y)/∂x² + ∂²f(x, y)/∂y²

其中，f(x, y) 是图像函数，∇² 是拉普拉斯算子。

#### 3.1.2 拉普拉斯滤波的数学推导

拉普拉斯滤波是通过卷积操作来实现的。拉普拉斯算子的卷积核为：

[-1 -1 -1]
[-1 8 -1]
[-1 -1 -1]

将该卷积核与图像函数进行卷积运算，即可得到拉普拉斯滤波的结果：

g(x, y) = f(x, y) * [-1 -1 -1]
                       [-1 8 -1]
                       [-1 -1 -1]

### 3.2 拉普拉斯滤波在图像锐化中的应用

#### 3.2.1 拉普拉斯滤波的卷积实现

在 MATLAB 中，可以使用 `conv2` 函数进行卷积运算。以下代码展示了如何使用拉普拉斯算子对图像进行锐化：

% 读取图像
I = imread('image.jpg');

% 拉普拉斯算子
laplacian = [-1 -1 -1; -1 8 -1; -1 -1 -1];

% 卷积运算