MATLAB图像锐化算法比较：不同算法的优缺点，如何选择最合适的算法，提升图像锐化效果

# 1. MATLAB图像锐化算法概述**

图像锐化是图像处理中一项重要的技术，用于增强图像细节和清晰度。MATLAB提供了一系列图像锐化算法，每种算法都有其独特的优点和缺点。本章将概述MATLAB中常用的图像锐化算法，为后续章节深入探讨其理论和实践奠定基础。

在图像锐化过程中，MATLAB算法通常通过应用卷积核（掩模）来操作图像。卷积核是一个包含权重值的矩阵，与图像像素进行逐元素相乘和求和，从而生成锐化的图像。不同的卷积核设计会产生不同的锐化效果，例如拉普拉斯、Sobel和Canny等算法使用的卷积核。

# 2. 常用图像锐化算法的理论与实践

图像锐化算法旨在增强图像中边缘和细节的对比度，从而改善图像的视觉效果。在MATLAB中，提供了多种图像锐化算法，每种算法都有其独特的理论基础和实现方式。本章将深入探讨三种常用的图像锐化算法：拉普拉斯锐化算法、Sobel锐化算法和Canny锐化算法。

### 2.1 拉普拉斯锐化算法

#### 2.1.1 理论基础

拉普拉斯锐化算法是基于图像的二阶导数来检测图像中的边缘和细节。其原理是使用一个拉普拉斯算子对图像进行卷积操作，该算子定义为：

[-1 -1 -1]
[-1  8 -1]
[-1 -1 -1]

当拉普拉斯算子与图像卷积时，它会突出图像中的边缘区域，因为这些区域具有较大的二阶导数。

#### 2.1.2 MATLAB实现

在MATLAB中，可以使用`imfilter`函数来实现拉普拉斯锐化算法。该函数的语法如下：

im_out = imfilter(im_in, H);

其中：

* `im_in`是输入图像。
* `H`是卷积核，即拉普拉斯算子。
* `im_out`是输出锐化图像。

以下代码展示了如何使用`imfilter`函数进行拉普拉斯锐化：

% 读取输入图像
im_in = imread('image.jpg');

% 定义拉普拉斯算子
H = [-1 -1 -1; -1 8 -1; -1 -1 -1];

% 进行拉普拉斯锐化
im_out = imfilter(im_in, H);

% 显示锐化后的图像
imshow(im_out);

### 2.2 Sobel锐化算法

#### 2.2.1 理论基础

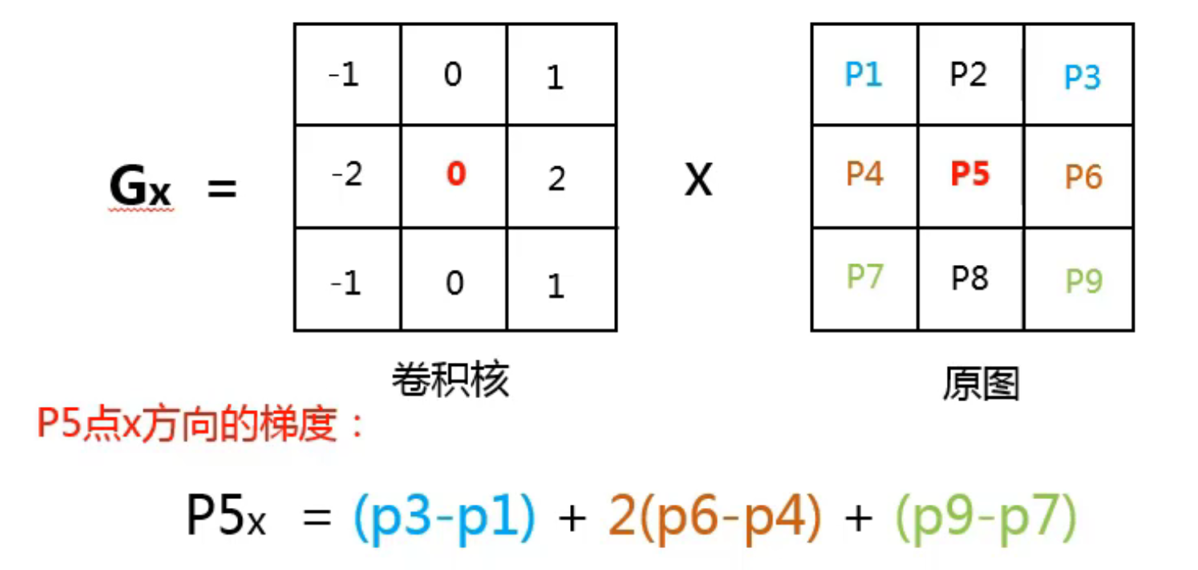
Sobel锐化算法是一种边缘检测算法，它通过计算图像梯度来检测图像中的边缘和细节。该算法使用两个Sobel算子，一个用于水平方向，另一个用于垂直方向。水平方向的Sobel算子定义为：

[-1 0 1]
[-2 0 2]
[-1 0 1]

垂直方向的Sobel算子定义为：

[-1 -2 -1]
[ 0  0  0]
[ 1  2  1]

#### 2.2.2 MATLAB实现

在MATLAB中，可以使用`imgradientxy`函数来实现Sobel锐化算法。该函数的语法如下：

[Gx, Gy] = imgradientxy(im_in);

其中：

* `im_in`是输入图像。
* `Gx`是水平方向的