MATLAB图像锐化最佳实践：提高图像锐化效率和效果的技巧，掌握图像锐化精髓

# 1. MATLAB图像锐化基础**

图像锐化是一种图像处理技术，用于增强图像的细节和清晰度。在MATLAB中，图像锐化可以通过空间域和频域算法实现。空间域算法直接操作图像像素，而频域算法则将图像转换为频域进行处理。

空间域锐化算法包括均值滤波、高斯滤波和拉普拉斯滤波。均值滤波通过计算像素邻域的平均值来平滑图像，从而降低噪声。高斯滤波使用加权平均值来平滑图像，权重随着距离像素的增加而减小。拉普拉斯滤波使用拉普拉斯算子来检测图像中的边缘，从而增强细节。

# 2. 图像锐化算法

### 2.1 空间域锐化算法

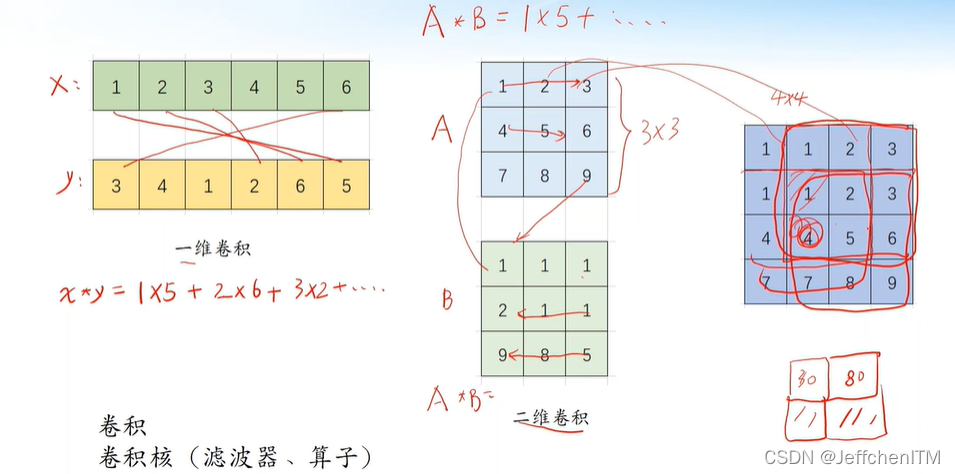
空间域锐化算法直接对图像像素进行操作，通过卷积核对图像进行滤波，增强图像边缘和细节。

#### 2.1.1 均值滤波

均值滤波是一种线性滤波器，通过计算卷积核内所有像素值的平均值来替换中心像素值。其卷积核通常为正方形或圆形，且所有元素值相等。均值滤波可以平滑图像噪声，但同时也会模糊图像边缘。

% 创建一个 3x3 均值滤波器
meanFilter = ones(3, 3) / 9;

% 对图像进行均值滤波
filteredImage = conv2(image, meanFilter, 'same');

#### 2.1.2 高斯滤波

高斯滤波也是一种线性滤波器，但其卷积核具有高斯分布形状。高斯滤波可以有效地平滑图像噪声，同时保留图像边缘。

% 创建一个 3x3 高斯滤波器
gaussianFilter = fspecial('gaussian', [3, 3], 1);

% 对图像进行高斯滤波
filteredImage = imfilter(image, gaussianFilter);

#### 2.1.3 拉普拉斯滤波

拉普拉斯滤波是一种二阶导数滤波器，其卷积核为：

[ 0 -1  0 ]
[-1  4 -1 ]
[ 0 -1  0 ]

拉普拉斯滤波可以增强图像边缘，但也会放大图像噪声。

% 创建一个 3x3 拉普拉斯滤波器
laplacianFilter = [-1 -1 -1; -1 8 -1; -1 -1 -1];

% 对图像进行拉普拉斯滤波
filteredImage = imfilter(image, laplacianFilter);

### 2.2 频域锐化算法

频域锐化算法将图像转换为频域，对频谱进行操作，然后将结果图像转换回空间域。

#### 2.2.1 傅里叶变换

傅里叶变换是一种数学变换，可以将图像从空间域转换为频域。在频域中，图像的低频分量对应于图像的平滑区域，而高频分量对应于图像的边缘和细节。

% 对图像进行傅里叶变换
FT = fft2(image);

#### 2.2.2 高通滤波

高通滤波器只允许高频分量通过，从而增强图像边缘和细节。

% 创建一个高通滤波器
highPassFilter = ones(size(FT));
highPassFilter(1:floor(size(FT, 1) / 2), 1:floor(size(FT, 2) / 2)) = 0;

% 对图像频谱进行高通滤波
FT_filtered = FT .* highPassFilter;

#### 2.2.3 反傅里叶变换

反傅里叶变换将图像频谱转换回空间域。

% 对图像频谱进行反傅里叶变换
filteredImage = ifft2(FT_filtered);

# 3. 图像锐化参数优化

### 3.1 锐化半径和强度

#### 3.1.1 锐化半径的影响

锐化半径决定了滤波器核的大小，它影响锐化的程度。较大的半径会产生更强的锐化效果，但同时也可能引入更多的噪声。

**代码块：**

% 创建一个高斯滤波器核