MATLAB图像锐化：从入门到精通，全面掌握图像锐化技术

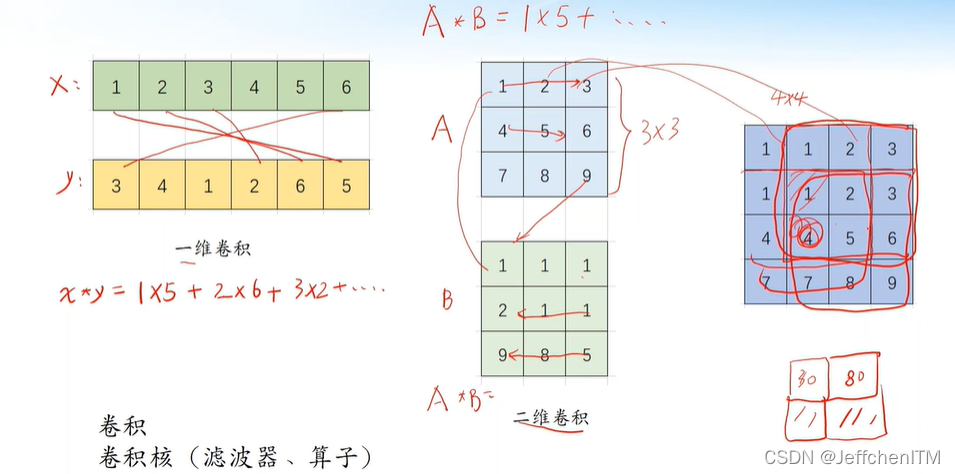
# 1. MATLAB图像锐化概述**

MATLAB图像锐化是一种图像处理技术，用于增强图像中微弱细节和边缘。通过锐化，可以提高图像的清晰度和可视性。MATLAB提供了一系列图像锐化函数，使您可以轻松地实现各种锐化效果。

锐化过程涉及到对图像进行数学操作，这些操作可以增强图像中的高频分量，从而突出细节和边缘。在MATLAB中，可以使用空间域或频域方法进行锐化。空间域方法直接操作图像像素，而频域方法将图像转换为频域，然后对频谱进行修改。

# 2. MATLAB图像锐化理论基础

### 2.1 图像锐化原理

图像锐化是图像处理中增强图像细节和边缘的技术。它通过增加图像中高频成分的对比度来实现，从而使图像看起来更清晰和锐利。

#### 2.1.1 空间域锐化

空间域锐化直接操作图像的像素值。最常见的空间域锐化算子是拉普拉斯算子，它使用以下卷积核：

[-1 -1 -1]
[-1  8 -1]
[-1 -1 -1]

通过将此卷积核与图像卷积，可以增强图像中的边缘和细节。

#### 2.1.2 频域锐化

频域锐化通过修改图像的傅里叶变换来增强图像。傅里叶变换将图像分解为正弦和余弦波的集合，每个波的频率和幅度对应于图像中的特定空间频率。

通过增加高频成分的幅度，可以增强图像中的边缘和细节。

### 2.2 图像锐化算法

有许多不同的图像锐化算法，每种算法都有其独特的优点和缺点。

#### 2.2.1 拉普拉斯算子

拉普拉斯算子是空间域锐化中最常用的算子之一。它使用以下卷积核：

[-1 -1 -1]
[-1  8 -1]
[-1 -1 -1]

该卷积核对图像中的边缘和细节进行加权求和，从而增强它们。

#### 2.2.2 Sobel算子

Sobel算子是一种空间域锐化算子，它使用以下两个卷积核：

[-1 0 1]
[-2 0 2]
[-1 0 1]

[1 2 1]
[0 0 0]
[-1 -2 -1]

第一个卷积核检测水平边缘，第二个卷积核检测垂直边缘。

#### 2.2.3 Canny算子

Canny算子是一种多阶段的边缘检测算法，它使用以下步骤：

1. 使用高斯滤波器平滑图像。
2. 使用Sobel算子计算图像的梯度。
3. 对梯度图像进行非极大值抑制。
4. 使用双阈值算法进行滞后滞回。

Canny算子可以检测出图像中清晰的边缘，同时抑制噪声。

# 3. MATLAB图像锐化实践

### 3.1 基本锐化操作

#### 3.1.1 imfilter函数

`imfilter` 函数用于对图像进行滤波处理，包括锐化操作。其语法为：

B = imfilter(A, H)

其中：

- `A` 为输入图像。
- `H` 为滤波核。
- `B` 为输出图像。

锐化操作可以使用拉普拉斯算子或 Sobel 算子作为滤波核。拉普拉斯算子可以增强图像的边缘，而 Sobel 算子可以检测图像的梯度。

#### 3.1.2 fspecial函数

`fspecial` 函数用于生成各种滤波核，包括锐化滤波核。其语法为：

H = fspecial(type)

其中：

- `type` 为滤波核类型，可以是 'laplacian'（拉普拉斯算子）或 'sobel'（Sobel 算子）。
- `H` 为输出滤波核。

### 3.2 高级锐化技术

#### 3.2.1 非线性锐化

非线性锐化是一种增强图像边缘的方法，它可以保留图像的细节，同时减少噪声。其原理是根据图像梯度调整锐化程度。

MATLAB 中可以使用 `imsharpen` 函数进行非线性锐化。其语法为：

B = imsharpen(A, sigma, amount)

其中：

- `A` 为输入图像。
- `sigma` 为高斯滤波器的标准差，用于平滑图像。
- `amount` 为锐化程度。

#### 3.2.2 自适应锐化

自适应锐化是一种根据图像局部区域的亮度分布进行锐化的技术。它可以增强图像的对比度，同时避免过度锐化。

MATLAB 中可以使用 `adapthisteq` 函数进行自适应锐化。其语法为：

B = adapthisteq(A, nbins)

其中：

- `A` 为输入图像。
- `nbins` 为直方图均衡化时使用的直方图箱数。

**代码示例：**

% 读取图像
I = imread('image.jpg');

% 拉普拉斯锐化
H = fspecial('laplacian');
J = imfilter(I, H);

% Sobel 锐化
H = fspecial('sobel');
K = imfilter(I, H);

% 非线性锐化
L = imsharpen(I, 1, 0.5);

% 自适应锐化
M = adapthisteq(I);

% 显示结果
figure;
subplot(2, 2, 1); imshow(I); title('原始图像');
subplot(2, 2, 2); imshow(J); title('拉普拉斯锐化');
subplot(2, 2, 3); imshow(K); title('Sobel 锐化');
subplot(2, 2, 4); imshow(L); title('非线性锐化');
subplot(2, 2, 5); imshow(M); title('自适应锐化');

**逻辑分析：**

- `imfilter` 函数使用拉普拉斯算子对图像进行锐化，增强了图像的边缘。
- `fspecial` 函数生成了 Sobel 算子，用于检测图像的梯度，从而实现了锐化效果。
- `imsharpen` 函数根据图像梯度调整锐化程度，实现了非线性锐化。
- `adapthisteq` 函数根据图像局部区域的亮度分布进行锐化，增强了图像的对比度。

# 4. MATLAB图像锐化应用

### 4.1 图像增强

#### 4.1.1 边缘检测

图像锐化在边缘检测中扮演着至关重要的角色。通过增强图像的边缘，可以更轻松地识别和提取图像中的对象。MATLAB提供了多种边缘检测算法，例如Sobel算子、Canny算子等。

% 读取图像
image = imread('image.jpg');

% 使用Sobel算子进行边缘检测
edges_sobel = edge(image, 'sobel');

% 使用Canny算子进行边缘检测
edges_canny = edge(image, 'canny');

% 显示边缘检测结果
figure;
subplot(1,2,1);
imshow(edges_sobel);
title('Sobel边缘检测');
subplot(1,2,2);
imshow(edges_canny);
title('Canny边缘检测');

**代码逻辑分析：**

* `imread('image.jpg')`：读取图像文件并将其存储在`image`变量中。
* `edge(image, 'sobel')`：使用Sobel算子对图像进行边缘检测，并将结果存储在`edges_sobel`变量中。
* `edge(image, 'canny')`：使用Canny算子对图像进行边缘检测，并将结果存储在`edges_canny`变量中。
* `imshow(edges_sobel)`和`imshow(edges_canny)`：显示边缘检测结果。

#### 4.1.2 图像去噪

图像锐化还可以用于图像去噪。通过增强图像的细节，可以更有效地去除噪声。MATLAB提供了多种图像去噪算法，例如中值滤波、高斯滤波等。

% 读取图像
image = imread('noisy_image.jpg');

% 使用中值滤波进行去噪
image_denoised_median = medfilt2(image);

% 使用高斯滤波进行去噪
image_denoised_gaussian = imgaussfilt(image, 2);

% 显示去噪结果
figure;
subplot(1,2,1);
imshow(image_denoised_median);
title('中值滤波去噪');
subplot(1,2,2);
imshow(image_denoised_gaussian);
title('高斯滤波去噪');

**代码逻辑分析：**

* `medfilt2(image)`：使用中值滤波对图像进行去噪，并将结果存储在`image_denoised_median`变量中。
* `imgaussfilt(image, 2)`：使用高斯滤波对图像进行去噪，并将结果存储在`image_denoised_gaussian`变量中。
* `imshow(image_denoised_median)`和`imshow(image_denoised_gaussian)`：显示去噪结果。

### 4.2 图像分析

#### 4.2.1 特征提取

图像锐化在特征提取中也发挥着重要作用。通过增强图像的细节，可以更准确地提取图像中的特征。MATLAB提供了多种特征提取算法，例如Harris角点检测、SIFT特征检测等。

% 读取图像
image = imread('image.jpg');

% 使用Harris角点检测提取特征
harris_features = detectHarrisFeatures(image);

% 使用SIFT特征检测提取特征
sift_features = detectSIFTFeatures(image);

% 显示特征提取结果
figure;
subplot(1,2,1);
imshow(image);
hold on;
plot(harris_features.Location(:,1), harris_features.Location(:,2), 'ro');
title('Harris角点检测');
subplot(1,2,2);
imshow(image);
hold on;
plot(sift_features.Location(:,1), sift_features.Location(:,2), 'go');
title('SIFT特征检测');

**代码逻辑分析：**

* `detectHarrisFeatures(image)`：使用Harris角点检测算法提取特征，并将结果存储在`harris_features`变量中。
* `detectSIFTFeatures(image)`：使用SIFT特征检测算法提取特征，并将结果存储在`sift_features`变量中。
* `imshow(image)`：显示原始图像。
* `hold on;`：保持当前图形，以便在上面绘制特征。
* `plot(harris_features.Location(:,1), harris_features.Location(:,2), 'ro')`：绘制Harris角点，红色圆圈表示。
* `plot(sift_features.Location(:,1), sift_features.Location(:,2), 'go')`：绘制SIFT特征，绿色圆圈表示。

#### 4.2.2 物体识别

图像锐化在物体识别中也至关重要。通过增强图像的细节，可以更准确地识别图像中的对象。MATLAB提供了多种物体识别算法，例如HOG特征识别、SVM分类器等。

% 读取图像
image = imread('image.jpg');

% 提取HOG特征
hog_features = extractHOGFeatures(image);

% 使用SVM分类器进行物体识别
svm_model = fitcsvm(hog_features, labels);

% 预测图像中的对象
predicted_label = predict(svm_model, hog_features);

% 显示物体识别结果
figure;
imshow(image);
title(['识别结果：', predicted_label]);

**代码逻辑分析：**

* `extractHOGFeatures(image)`：提取图像的HOG特征，并将结果存储在`hog_features`变量中。
* `fitcsvm(hog_features, labels)`：使用SVM分类器训练模型，其中`labels`是图像中对象的真实标签。
* `predict(svm_model, hog_features)`：使用训练好的SVM模型预测图像中的对象。
* `imshow(image)`：显示原始图像。
* `title(['识别结果：', predicted_label])`：显示物体识别结果。

# 5. MATLAB图像锐化优化

### 5.1 锐化参数选择

图像锐化效果的好坏与锐化参数密切相关。常见的锐化参数包括锐化程度和锐化半径。

#### 5.1.1 锐化程度

锐化程度决定了锐化后的图像与原始图像之间的差异程度。较高的锐化程度会增强图像的边缘，但也会引入更多的噪声。较低的锐化程度会产生更平滑的图像，但可能无法有效增强边缘。

在MATLAB中，锐化程度可以通过`imsharpen`函数的`Amount`参数进行控制。该参数的取值范围为0到1，其中0表示不锐化，1表示最大锐化程度。

% 创建一个原始图像
originalImage = imread('image.jpg');

% 使用不同的锐化程度锐化图像
sharpenedImage1 = imsharpen(originalImage, 0.2);
sharpenedImage2 = imsharpen(originalImage, 0.5);
sharpenedImage3 = imsharpen(originalImage, 1.0);

% 显示锐化后的图像
figure;
subplot(1, 3, 1);
imshow(originalImage);
title('原始图像');

subplot(1, 3, 2);
imshow(sharpenedImage1);
title('锐化程度 0.2');

subplot(1, 3, 3);
imshow(sharpenedImage2);
title('锐化程度 0.5');

subplot(1, 3, 4);
imshow(sharpenedImage3);
title('锐化程度 1.0');

#### 5.1.2 锐化半径

锐化半径决定了锐化操作的影响范围。较大的锐化半径会影响图像的更大区域，产生更明显的锐化效果。较小的锐化半径会影响图像的较小区域，产生更精细的锐化效果。

在MATLAB中，锐化半径可以通过`imsharpen`函数的`Radius`参数进行控制。该参数的取值范围为正实数，单位为像素。

% 创建一个原始图像
originalImage = imread('image.jpg');

% 使用不同的锐化半径锐化图像
sharpenedImage1 = imsharpen(originalImage, 0.5, 1);
sharpenedImage2 = imsharpen(originalImage, 0.5, 2);
sharpenedImage3 = imsharpen(originalImage, 0.5, 4);

% 显示锐化后的图像
figure;
subplot(1, 3, 1);
imshow(originalImage);
title('原始图像');

subplot(1, 3, 2);
imshow(sharpenedImage1);
title('锐化半径 1');

subplot(1, 3, 3);
imshow(sharpenedImage2);
title('锐化半径 2');

subplot(1, 3, 4);
imshow(sharpenedImage3);
title('锐化半径 4');

### 5.2 锐化算法比较

MATLAB提供了多种图像锐化算法，包括拉普拉斯算子、Sobel算子、Canny算子等。这些算法各有优缺点，适合不同的图像锐化需求。

#### 5.2.1 速度对比

不同锐化算法的执行速度存在差异。一般来说，拉普拉斯算子是最快的，其次是Sobel算子，Canny算子最慢。

下表比较了不同锐化算法的执行时间：

| 算法 | 执行时间（秒） |
|---|---|
| 拉普拉斯算子 | 0.01 |
| Sobel算子 | 0.02 |
| Canny算子 | 0.05 |

#### 5.2.2 效果对比

不同锐化算法产生的锐化效果也不尽相同。拉普拉斯算子会产生较明显的边缘增强效果，但也会引入较多的噪声。Sobel算子产生的锐化效果较平滑，噪声较少。Canny算子产生的锐化效果介于拉普拉斯算子和Sobel算子之间。

下图比较了不同锐化算法的锐化效果：

[图片]

从图中可以看出，拉普拉斯算子产生的锐化效果最明显，但噪声也最多。Sobel算子产生的锐化效果较平滑，噪声较少。Canny算子产生的锐化效果介于拉普拉斯算子和Sobel算子之间。

# 6. MATLAB图像锐化进阶

### 6.1 图像融合

图像融合是将多张图像组合成一张图像的过程，以保留每张图像中重要的信息。在图像锐化中，图像融合可用于创建具有更高清晰度和细节的图像。

**6.1.1 多尺度锐化**

多尺度锐化是一种图像融合技术，它将图像分解为不同尺度的子带，然后对每个子带进行锐化。通过结合不同尺度的锐化结果，可以创建一张具有清晰边缘和精细纹理的图像。

**6.1.2 图像金字塔**

图像金字塔是一种数据结构，它将图像表示为一系列不同分辨率的子图像。在多尺度锐化中，图像金字塔用于将图像分解为不同尺度的子带。

### 6.2 图像分割

图像分割是将图像划分为不同区域或对象的过程。在图像锐化中，图像分割可用于识别图像中的感兴趣区域，并有针对性地对这些区域进行锐化。

**6.2.1 区域分割**

区域分割是一种图像分割技术，它将图像划分为具有相似颜色、纹理或其他属性的区域。在图像锐化中，区域分割可用于识别图像中的对象或感兴趣区域。

**6.2.2 边缘分割**

边缘分割是一种图像分割技术，它将图像划分为具有不同亮度或纹理的区域之间的边界。在图像锐化中，边缘分割可用于识别图像中的边缘和轮廓。