性能优化：Origin FFT提升计算效率的三大策略


参考资源链接：[Origin软件快速傅里叶变换(FFT)实操教程](https://wenku.csdn.net/doc/f4sz0rt6pp?spm=1055.2635.3001.10343)
# 1. Origin FFT的基本原理和性能挑战

快速傅里叶变换（FFT）是数字信号处理中不可或缺的核心算法，由其前身离散傅里叶变换（DFT）衍生而来。尽管FFT算法在理论与实践中得到了广泛应用，但仍然面临着性能上的挑战。本章将探讨FFT的基本原理，包括DFT向FFT的演进过程，以及分治策略在FFT中的具体应用。此外，本章还将剖析FFT性能瓶颈的成因，包括算法的时间复杂度分析，以及在现实世界应用中导致性能损失的具体场景。最后，针对目前FFT在计算效率和资源利用上的不足，本章将探讨可能的优化方向和理论基础。

# 2. 理论基础：FFT算法的优化空间

### 2.1 FFT算法的工作原理

#### 2.1.1 DFT与FFT的关系

离散傅里叶变换（DFT）是数字信号处理中的基本工具，用于分析时域信号在频域的表示。然而，DFT的计算复杂度为O(N^2)，其中N是数据点的数量，这在处理大量数据时显得非常低效。快速傅里叶变换（FFT）是DFT的一个高效算法实现，其将DFT的计算复杂度降低到O(NlogN)。

DFT的计算公式如下：
\[X(k) = \sum_{n=0}^{N-1} x(n) \cdot e^{-\frac{j2\pi kn}{N}}\]
其中，\(x(n)\)是输入信号，\(X(k)\)是其频域表示，\(j\)是虚数单位。

FFT算法利用了DFT的周期性和对称性，将原始的DFT分解成更小的DFTs进行计算。这个分解过程通常通过分治策略实现，比如著名的Cooley-Tukey算法。

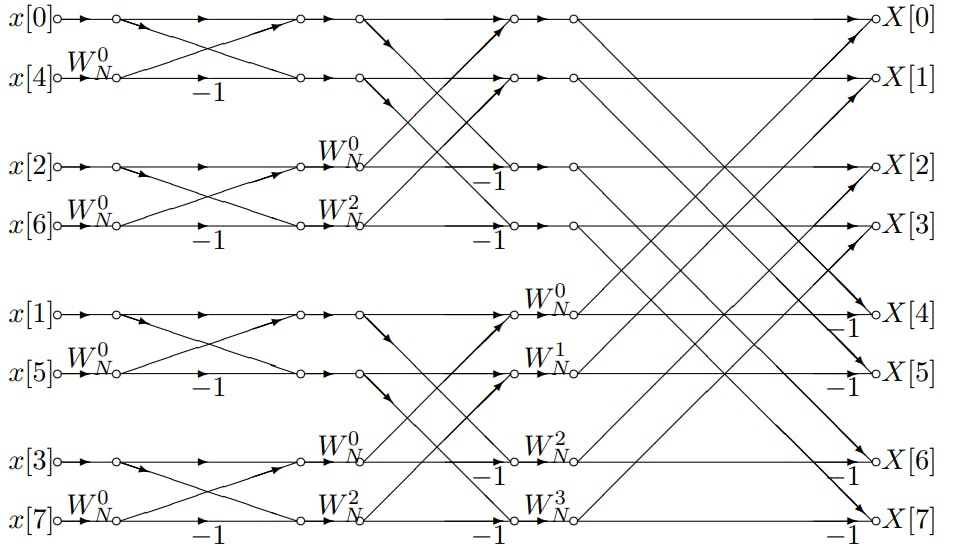
#### 2.1.2 分治策略在FFT中的应用

分治策略是FFT算法的核心思想。在Cooley-Tukey FFT算法中，数据首先被分组，每组包含N/2个点，其中N是2的幂次。然后，这些子组在各自的频域中被处理，最终这些子组的频域表示被组合起来，形成最终的DFT结果。

具体步骤包括：
1. 将输入数据序列\(x(n)\)按照奇数和偶数索引分开。
2. 分别对偶数索引序列\(x_{even}(n)\)和奇数索引序列\(x_{odd}(n)\)执行DFT。
3. 将两个DFT结果组合起来，得到最终的FFT结果。

分治策略通过这样的分解，大大减少了计算量，并使FFT能够高效地应用于各种场景。

### 2.2 FFT性能瓶颈分析

#### 2.2.1 复杂度分析

尽管FFT算法的复杂度已经显著降低到了\(O(NlogN)\)，但在处理非常大的数据集时，性能瓶颈依旧存在。主要瓶颈包括：
- 内存带宽限制：在将数据读入处理器进行计算时，内存的读写速度可能成为瓶颈。
- 计算单元利用率：由于FFT计算中存在数据依赖性，单个计算单元可能在等待数据时处于空闲状态。

#### 2.2.2 实际应用中的性能损失点

在实际应用FFT时，性能损失点可能出现在：
- 数据输入输出（I/O）：频繁的I/O操作可能导致CPU等待I/O操作完成，影响整体性能。
- 缓存命中率低：算法如果不能有效利用缓存，则会导致处理器访问主存的频率增加，造成性能下降。

### 2.3 理论优化方向探讨

#### 2.3.1 算法改进的可能性

针对FFT的性能瓶颈，可以从多个方面进行算法改进：
- 采用更有效的数据预处理和后处理方法，减少不必要的计算。
- 对FFT算法进行结构上的调整，例如使用分块FFT，以更好地适应现代处理器的缓存层次结构。

#### 2.3.2 硬件加速理论基础

硬件加速是提升FFT性能的重要方向之一，具体包括：
- 使用专门的硬件加速器，例如FPGA、ASIC或GPU，这些硬件可以并行执行计算，显著提升性能。
- 研究CPU与GPU间的异构计算模型，优化数据在不同处理单元间的传输和处理。

接下来章节会深入探讨实践策略中的一些具体技术，如何进一步优化FFT性能，包括数据结构优化、并行计算的应用和专用硬件的利用。

# 3. 实践策略一：数据结构优化

### 3.1 输入输出数据的优化处理

数字信号处理（DSP）中的快速傅里叶变换（FFT）是一种计算离散傅里叶变换（DFT）及其逆变换的算法。在实际应用中，数据的输入输出操作占据了FFT处理过程中的重要地位。对输入输出数据进行优化处理，能够显著提高FFT算法的整体性能和计算效率。

#### 3.1.1 数据预处理技巧

在进行FFT运算之前，数据预处理是优化FFT输入输出的一个重要步骤。预处理的目标是尽量减少FFT算法的计算负担，或提前排除无用数据。以下是几个有效的数据预处理技巧：

1. **填充（Padding）**: 填充是为了使数据长度达到2的幂次，从而利用基于快速傅里叶变换（FFT）的高效算法。但是，过度填充可能会引入不必要的零值，这可能会降低算法效率，需要根据FFT算法的具体实现进行权衡。

2. **缩放（Scaling）**: 在FFT计算过程中，由于频谱泄露、窗函数等因素，FFT输出的幅度可能会受到干扰。适当的缩放可以将结果调整到合适的大小，以符合实际应用场景的要求。

3. **窗函数（Windowing）**: 为了减少频谱泄露，可以使用窗函数处理输入数据。窗函数通过调整数据边界的幅度来减少数据跳变，从而降低泄露现象。

代码块示例：

import numpy as np

# 输入数据准备
data = np.random.rand(1024)  # 假设有一组长度为1024的输入数据
data = data * np.hamming(len(data))  # 使用汉明窗减少频谱泄露
padded_data = np.fft.fftshift(np.fft.fft(data))  # FFT计算并进行频移

在上述代码中，首先生成了一组随机数据，然后应用了汉明窗以减少频谱泄露。最后，通过`fftshift`和`fft`函数完成了数据的FFT计算。

#### 3.1.2 数据存储格式的选择

选择合适的数据存储格式对于优化FFT的输入输出同样重要。存储格式不仅影响数据读取速度，而且也影响到数据处理的效率。

1. **连续存储（Contiguous Storage）**: 连续存储格式如NumPy数组，能够保证良好的缓存利用，从而提高数据处理速度。

2. **交错存储（Interleaved Storage）与分离存储（Separate Storage）**: 对于多维信号，交错存储和分离存储各有优势。交错存储格式可以减少内存访问次数，而分离存储格式有利于并行处理。

3. **内存对齐（Memory Alignment）**: 内存对齐可以提高现代处理器的性能，确保数据在高速缓存和处理器之间的传输效率。

表格展示不同数据存储格式的比较：

| 存储格式 | 描述 | 优点 | 缺点 |
| --- | --- | --- | --- |
| 连续存储 | 数据在内存中连续存放 | 缓存命中率高，处理速度快 | 占用较多连续内存空间 |
| 交错存储 | 多维数据的每一维度连续存放 | 减少内存访问次数 | 数据处理复杂度高 |
| 分离存储 | 各维度数据分别存储 | 并行处理效率高 | 占用更多内存空间 |
| 内存对齐 | 数据按照处理器要求对齐存储 | 优化内存读写性能 | 需要额外处理，可能导致资源浪费 |

### 3.2 内存管理的改进

随着FFT算法规模的增大，内存管理成为提高性能的关键。良好的内存管理不仅可以减少内存使用，还能降低内存碎片化，提升缓存利用率。

#### 3.2.1 缓存友好型设计

缓存友好型设计是指让数据尽可能地被存储在CPU缓存中，这样可以加快数据的读取速度，减少访问主内存的次数。对于FFT算法来说，可以采取以下措施实现缓存优化：

1. **输入数据的分块处理（Blocking）**: 将大尺寸FFT分解成若干小尺寸的FFT，能够使得每一块数据频繁地在缓存中利用，减少主内存访问。

2. **数据重排序（Data Reordering）**: 对