Origin FFT在数据平滑中的应用：细节与技巧


参考资源链接：[Origin软件快速傅里叶变换(FFT)实操教程](https://wenku.csdn.net/doc/f4sz0rt6pp?spm=1055.2635.3001.10343)
# 1. Origin FFT简介

## 1.1 原理概述
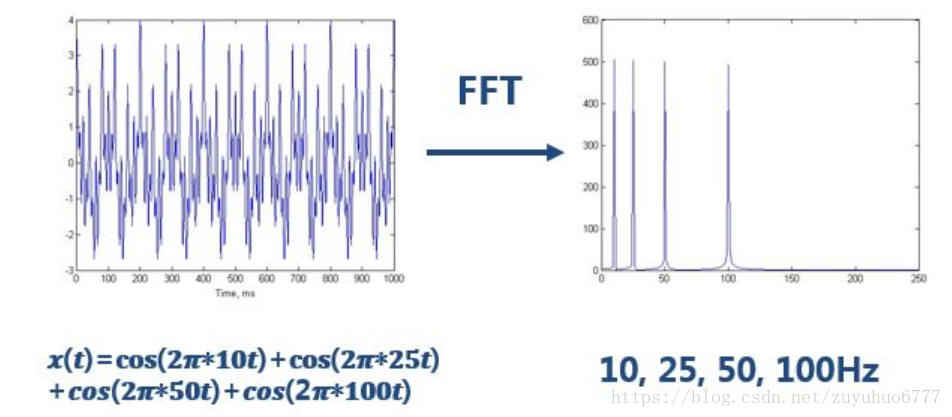
Origin FFT（快速傅里叶变换）是信号处理中的一种算法，用于将时间域上的离散信号转换到频率域上。通过这种变换，可以更容易地分析信号的频率成分，识别周期性波动，以及进行噪声过滤等操作。

## 1.2 历史背景与发展
FFT的概念最早由数学家和工程师们提出，并经过几十年的发展，已经成为数字信号处理领域不可或缺的工具之一。它的出现极大地提升了信号分析的速度和效率，特别是在处理大数据集时。

## 1.3 应用场景
在电子工程、通信、地震学、语音分析以及医学成像等多个领域，Origin FFT均有着广泛的应用。它可以帮助科研人员和工程师们更清晰地理解复杂的信号结构，从而做出更为精确的数据处理和决策。

Origin FFT不只是一个简单的技术手段，它的应用背后是复杂的数学理论支撑。接下来的章节将深入探讨数据平滑的理论基础，为理解FFT在数据处理中的作用打下坚实的基础。

# 2. 数据平滑的理论基础

## 2.1 数据平滑的定义和目的

### 2.1.1 数据平滑的数学原理

数据平滑，亦称为数据平滑处理或滤波处理，是一种用于降低数据集中噪声或随机波动的技术。其核心在于通过数学算法将数据序列中的高频分量（即噪音部分）减弱，保留低频分量（即数据的趋势或周期性特征），进而使数据序列变得平滑。这一过程中，最重要的是数学原理的应用，其中最常见的数学工具包括傅里叶变换（FFT）、移动平均法等。

傅里叶变换将信号从时域转换到频域，通过滤除不需要的频率成分再转换回时域，达到去噪的目的。移动平均法通过对连续数据点进行平均，减少随机波动的影响，从而实现数据的平滑。

### 2.1.2 数据平滑在信号处理中的作用

在信号处理领域，数据平滑可以应用于各种场景，例如数据去噪、趋势分析和模式识别等。去噪是为了减少环境噪声和测量误差导致的随机波动，而趋势分析则是为了揭示数据的整体走向。数据平滑技术可以有效突出信号的主要特征，帮助我们更准确地识别和提取信号中的有用信息，降低误判和误差的可能性。

## 2.2 常见的数据平滑技术

### 2.2.1 移动平均法

移动平均法是一种简单且广泛应用于时间序列数据平滑的技术。它通过计算数据点的一组连续值的平均来创建新的数据点。常见的移动平均法包括简单移动平均（SMA）、加权移动平均（WMA）和指数移动平均（EMA）。简单移动平均通过均等地对待所有数据点，而加权移动平均则赋予最近的数据点更高的权重。指数移动平均对最近的数据点赋予更高的权重，并且衰减因子的使用使得其在处理短期趋势时更灵活。

### 2.2.2 滑动平均滤波器

滑动平均滤波器，又称作低通滤波器，是一种在数字信号处理中常用的平滑技术。该方法通过计算输入信号在一定时间窗口内的平均值来生成输出信号。滑动平均滤波器的性能可以通过改变窗口大小来进行调整。较小的窗口在平滑的同时保留较多的信号细节，而较大的窗口则提供更强的噪声抑制能力但牺牲了更多的信号细节。

### 2.2.3 高斯平滑

高斯平滑是基于高斯分布理论的一种数据平滑技术，它利用高斯函数作为滤波核对数据进行平滑。在高斯平滑中，权重是根据高斯函数分配的，这使得紧邻的数据点贡献更多的权重，而距离更远的数据点贡献逐渐减少。因此，高斯平滑对于消除高频噪声和保持数据的基本趋势非常有效，同时还能保持信号的边缘信息不被过度模糊。

# 3. Origin FFT在数据平滑中的应用

## 3.1 FFT的基本概念和原理

### 3.1.1 FFT的数学背景

快速傅里叶变换（Fast Fourier Transform，FFT）是一种高效计算离散傅里叶变换（Discrete Fourier Transform，DFT）及其逆变换的算法。FFT是DFT的快速算法版本，由于其计算复杂度的显著降低，它在数字信号处理、图像处理、大数据分析等领域得到了广泛应用。

DFT的核心思想是将时间域（或空间域）的信号转换到频域，这样可以分析信号的频率成分。FFT之所以受到青睐，是因为它显著减少了DFT的运算次数。传统的DFT需要O(N^2)次复数乘法和加法运算，而使用FFT算法之后，运算次数可以降低到O(NlogN)级别。

### 3.1.2 FFT的计算方法和优势

FFT的计算方法通常分为两大类：迭代算法和分治算法。迭代算法如Cooley-Tukey算法，适用于长度为2的幂次的序列；而分治算法，如Winograd算法和Good-Thomas算法，则能够处理更一般的情况。

FFT的优势在于其高效性，不仅减少了运算次数，还减少了运算过程中的舍入误差，使得在实际应用中能够获得更准确的结果。此外，FFT也方便了