案例分析：噪声信号分离与识别的Origin FFT方法


参考资源链接：[Origin软件快速傅里叶变换(FFT)实操教程](https://wenku.csdn.net/doc/f4sz0rt6pp?spm=1055.2635.3001.10343)
# 1. 噪声信号分离与识别的基本概念

在现代信息处理领域，准确地从采集到的信号中分离出噪声是至关重要的。噪声信号的识别和分离不仅仅是信号处理的基础，而且对于提高数据质量、改善系统性能至关重要。本章将对噪声信号分离与识别的基本概念进行简要介绍，为读者提供噪声信号处理技术的入门知识。

噪声可以定义为在通信、信号采集和处理过程中，对有用信号造成干扰的不期望的随机信号。噪声的来源多样，包括但不限于电子设备的内在噪声、环境噪声、背景噪音等。噪声信号的分离与识别技术的目的是从混合信号中提取出有用的信号成分，尽可能地减少噪声的影响。

信号与噪声的分离通常依赖于信号处理技术，如滤波器设计、傅里叶变换等方法。在后续章节中，我们将详细探讨这些技术的理论基础和实际应用。理解噪声信号分离与识别的基本概念是掌握后续复杂技术的前提，因此，本章是全文的理论基础。

# 2. 快速傅里叶变换(FFT)的理论基础

### 2.1 傅里叶变换简介

傅里叶变换是信号处理中的一项基础且重要的数学工具，它允许我们分析信号在不同频率上的成分。这一理论不仅为我们提供了一种将时域信号转换到频域的方法，而且也让我们能够理解和操作信号的频谱特性。

#### 2.1.1 连续时间信号的傅里叶变换

对于连续时间信号，其傅里叶变换由以下积分表示：

$$ X(f) = \int_{-\infty}^{\infty} x(t) e^{-j2\pi ft} dt $$

这个公式说明，任何连续时间信号都可以被看作是不同频率的正弦波的无限叠加。其中 $X(f)$ 是信号 $x(t)$ 的频谱表示，$f$ 是频率变量，$j$ 是虚数单位。

连续时间信号的傅里叶变换告诉我们信号在各个频率上的能量分布，这对于了解信号的本质特性至关重要。傅里叶变换不仅限于理论研究，在实际工程应用中，比如在通信、音频处理和医学成像等领域都扮演着重要角色。

#### 2.1.2 离散时间信号的傅里叶变换

在数字信号处理领域，我们经常处理的是离散时间信号。离散时间信号的傅里叶变换（DTFT）定义如下：

$$ X(e^{j\omega}) = \sum_{n=-\infty}^{\infty} x[n] e^{-j\omega n} $$

其中，$X(e^{j\omega})$ 是 $x[n]$ 的傅里叶变换，$\omega$ 是角频率。DTFT 给出了离散时间信号在各个连续频率上的频率谱。

DTFT 在实际应用中非常有用，但它要求对无限长的信号进行计算，这在现实中是不可能的。为了解决这个问题，通常会采用离散傅里叶变换（DFT），它是DTFT的有限长序列近似。

### 2.2 快速傅里叶变换(FFT)原理

#### 2.2.1 FFT算法的发展与优势

快速傅里叶变换（FFT）是一种高效计算DFT的算法。它是由James Cooley和John Tukey在1965年提出的，并迅速成为数字信号处理的核心技术之一。FFT算法相较于直接计算DFT的复杂度大大降低，从 $O(N^2)$ 下降到 $O(N \log N)$，其中 $N$ 是信号长度。这使得FFT在处理大量数据时具有显著的速度优势。

FFT的出现不仅提高了计算效率，而且还允许工程师和研究者实时地分析信号的频谱。这个能力在需要快速响应的应用中至关重要，比如在声纳、雷达和通信系统等领域。

#### 2.2.2 FFT的数学原理和实现过程

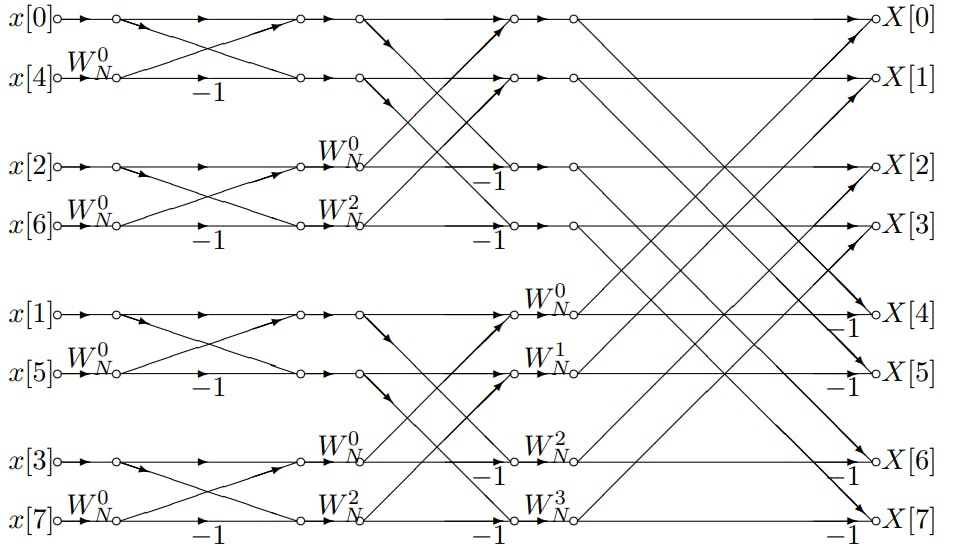
FFT算法的实现依赖于信号样本的周期性和对称性。最著名的FFT算法之一是Cooley-Tukey算法，它适用于样本长度是2的幂次的情况。该算法通过分治策略将原始DFT分解为更小的DFT子问题，然后递归地解决这些子问题。

一个简单的FFT实现步骤如下：

1. 输入时域信号 $x[n]$。
2. 确定是否符合FFT的长度要求，如样本点数是否为2的幂次。
3. 将信号分成偶数索引和奇数索引两部分。
4. 对这两部分分别递归地执行FFT操作。
5. 合并结果，通过旋转因子来调整相位。

### 2.3 噪声信号在频域中的表示

#### 2.3.1 噪声类型及其频域特性

在信号处理中，噪声通常表示那些不期望的随机或背景信号。噪声可以分为很多种，包括白噪声、粉红噪声、布朗噪声等。每种噪声都有其特定的频谱特性，而FFT可以将这些噪声在频域中表示出来。

- **白噪声**：在整个频谱范围内具有恒定的功率谱密度。
- **粉红噪声**：功率谱密度随着频率的降低呈1/f衰减。
- **布朗噪声**：功率谱密度随频率的平方成反比衰减。

通过FFT，我们可以观察和测量这些噪声的功率谱，从而对噪声的类型和特性有一个量化的了解。

#### 2.3.2 信号分离中的频域滤波方法

频域滤波是噪声分离中的一种常见技术。它利用FFT将信号从时域转换到频域，然后应用滤波器来抑制噪声成分。这种滤波器可以设计为带通、低通、高通或带阻滤波器，取决于我们希望保留或去除的信号部分。

滤波器的设计和应用通常涉及以下步骤：

1. 对信号应用FFT得到频谱。
2. 设计合适的频域滤波器。
3. 将滤波器应用于信号频谱。
4. 对滤波后的频谱应用逆FFT得到时域信号。

通过这种处理，我们可以有效地分离出有用的信号成分，同时抑制噪声。这一技术在无线通信、生物医学信号处理等领域尤其重要，因为它们往往需要在信号中剔除噪声干扰，提高信号的清晰度和准确性。

在接下来的章节中，我们将探讨FFT在特定软件工具中的应用，以及在噪声信号分离与识别中的实践案例。

# 3. Origin软件在信号处理中的应用

Origin软件是数据分析和科学可视化领域广泛使用的工具之一，它提供了强大的数据处理和图形绘制功能，尤其在信号处理领域中，Origin可以通过其直观的操作界面和丰富的分析工具，帮助工程师和科研人员有效地执行信号的频域分析和可视化